普通求素数和线性筛素数

傻瓜解法--n,n/2

#include<stdio.h>
int main()
{
  int i,n;
  while(scanf("%d",&n)==1)
  { for(i=2;i<n;i++)
         if(n%i==0)    break; 
    if(i==n)    printf("YES
");
    else           printf("NO
");
  }
}

这是理所当然的想法，按照素数的定义，除了1和它本身没有其他的因数，就是素数。

这种解法的缺点就是红色标注那里，i<n，或者有的是i<n....这种循环规模n稍微大点，运行就会超时。

普通解法--sqrt(n)

#include<stdio.h>
#include<math.h>
int main()
{ int i,n,x;
  while(scanf("%d",&n)==1)
  { x=(int)sqrt(n);
    for(i=2;i<=x;i++)
         if(n%i==0)    break; 
    if(i>x)    printf("YES
");
    else           printf("NO
");
  }
}

这里循环取到sqrt(n)，效率改进不少了...但显然还是不够理想。

普通筛选法--埃拉托斯特尼筛法

先简单说一下原理：

基本思想：素数的倍数一定不是素数
实现方法：用一个长度为N+1的数组保存信息（0表示素数，1表示非素数），先假设所有的数都是素数（初始化为0），从第一个素数2开始，把2的倍数都标记为非素数（置为1），一直到大于N；然后进行下一趟，找到2后面的下一个素数3，进行同样的处理，直到最后，数组中依然为0的数即为素数。
说明：整数1特殊处理即可。

举个例子，N=20时，演示如下图：

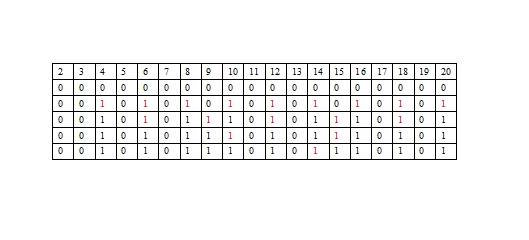
最后数组里面还是0的就是素数了...

代码实现如下：

prime[]用来保存得到的素数 prime[] = {2,3,5,7,11,.........} tot 是当前得到的素数的个数 check ：0表示是素数  1表示合数

memset(check, 0, sizeof(check));
int tot = 0;
for (int i = 2; i <= n; ++i)
{
  if (!check[i])
  {
    prime[tot++] = i;
  }
  for (int j = i+i; j <= n; j += i)
  {
    check[j] = 1;
  }
}

此筛选法的时间复杂度是O(nloglogn) 空间复杂度是O(n)

不足之处也比较明显，手动模拟一遍就会发现，很多数被处理了不止1遍，比如6，在素数为2的时候处理1次，为3时候又标记一次，因此又造成了比较大的不必要处理...那有没有改进的办法呢...就是下面改进之后的筛法...

线性筛法--欧拉筛法

#include<cstdio>
#include<cstring>
#define MAXN 100005
#define MAXL 1299710
int prime[MAXN];
int check[MAXL];

int tot = 0;
memset(check, 0, sizeof(check));
for (int i = 2; i < MAXL; ++i)
{
  if (!check[i])
  {
    prime[tot++] = i;
  }
  for (int j = 0; j < tot; ++j)
  {
    if (i * prime[j] > MAXL)
    {
      break;
    }
    check[i*prime[j]] = 1;
    if (i % prime[j] == 0)
    {
      break;
    }
  }
}

精华就在于红色标注那两处，它们保证每个合数只会被它的最小质因数筛去，因此每个数只会被标记一次，所以时间复杂度是O(n)

还是按上面的例子进行一遍模拟：N=20

此过程中保证了两点：

1、合数一定被干掉了...

2、每个数都没有被重复地删掉

P.S.  另一种方法和解释

#include <cstring>
using namespace std;
int prime[1100000],primesize,phi[11000000];
bool isprime[11000000];
void getlist(int listsize)
{
    memset(isprime,1,sizeof(isprime));
    isprime[1]=false;
    for(int i=2;i<=listsize;i++)
    {
        if(isprime[i])prime[++primesize]=i;
         for(int j=1;j<=primesize&&i*prime[j]<=listsize;j++)
         {
            isprime[i*prime[j]]=false;
            if(i%prime[j]==0)break;
        }
    }
}

prime[]数组中的素数是递增的,当i能整除prime[j]，那么i*prime[j+1]这个合数肯定被prime[j]乘以某个数筛掉。
   因为i中含有prime[j],prime[j]比prime[j+1]小，即i=k*prime[j]，那么i*prime[j+1]=(k*prime[j])*prime
   [j+1]=k’*prime[j]，接下去的素数同理。所以不用筛下去了。因此，在满足i%prime[j]==0这个条件之前以及第一次
   满足改条件时,prime[j]必定是prime[j]*i的最小因子。

引申--求欧拉函数

在数论，对正整数n，欧拉函数是小于或等于n的数中与n互质的数的数目。此函数以其首名研究者欧拉命名，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4，因为1,3,5,7均和8互质。

求欧拉函数的方法只需在上面的程序中稍有改动即可

#include<cstdio>
#include<cstring>
#define MAXN 100005
#define MAXL 1299710
int prime[MAXN];
int check[MAXL];
int phi[MAXL];
int tot = 0;
phi[1] = 1;
memset(check, 0, sizeof(check));
for (int i = 2; i < MAXL; ++i)
{
  if (!check[i])
  {
    prime[tot++] = i;
    phi[i] = i - 1;
  }
  for (int j = 0; j < tot; ++j)
  {
    if (i * prime[j] > MAXL)
    {
      break;
    }
    check[i*prime[j]] = 1;
    if (i % prime[j] == 0)
    {
      phi[i*prime[j]] = phi[i] * prime[j];
      break;
    }else
    {
      phi[i*prime[j]] = phi[i] * (prime[j]-1);
    }
  }
}

若是素数，那么从1~n-1都是和它互质的数，所以phi(i) = i - 1;

另外两个是积性函数的公式和欧拉函数的特性。

【转载】：http://www.cnblogs.com/grubbyskyer/p/3852421.html