愉快的周末结束啦,今日每日一题中等难度,虽然写出来了,但是没有官网的运行速度快,来记录啦!!!

题目描述:
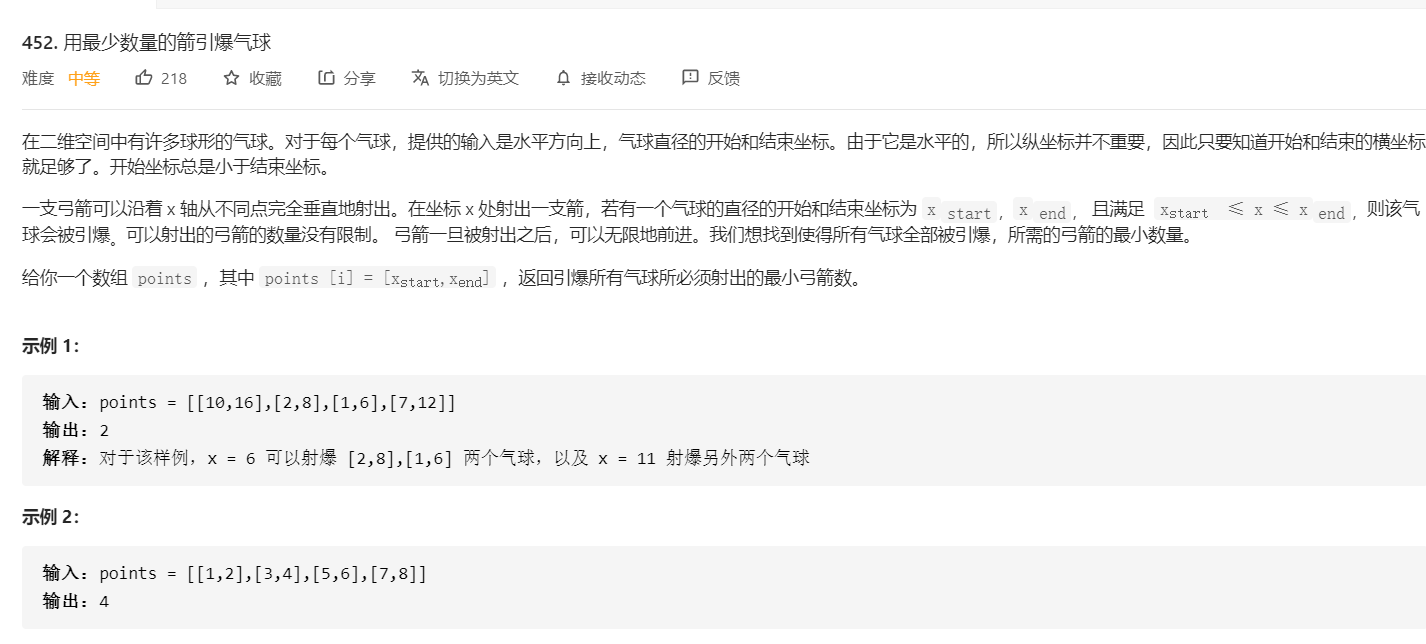

先来记录一下我的做题思路和代码吧:
思路:如果两个气球能同时被戳破,则这两个气球的位置坐标必然有重合的地方,所以我们可以计算他们的重合坐标
。但是在现在这个乱序的情况下,计算公共坐标还需要存储计算出来的重合坐标啊,防止后续又需要使用,为了防
止这个情况,我们先对数组进行排序。然后再计算重合坐标。代码如下:
public int findMinArrowShots(int[][] points) {
if(points.length==0){
return 0;
}
Arrays.sort(points,(a,b)->{
if(a[0]<b[0]){
return -1;
}
if(a[0]>b[0]){
return 1;
}
return 0;
});
int result=1;
int[] tmpIndex=points[0];
for(int i=1;i<points.length;i++){
if(tmpIndex[1]>=points[i][0]){
//计算重合坐标
tmpIndex[0]=Math.max(tmpIndex[0],points[i][0]);
tmpIndex[1]=Math.min(tmpIndex[1],points[i][1]);
continue;
}
result++;
tmpIndex=points[i];
}
return result;
}
运行速度如下:
这速度果然感人,所以我决定再去官网学习一下,果然还是有很大的优化之处:
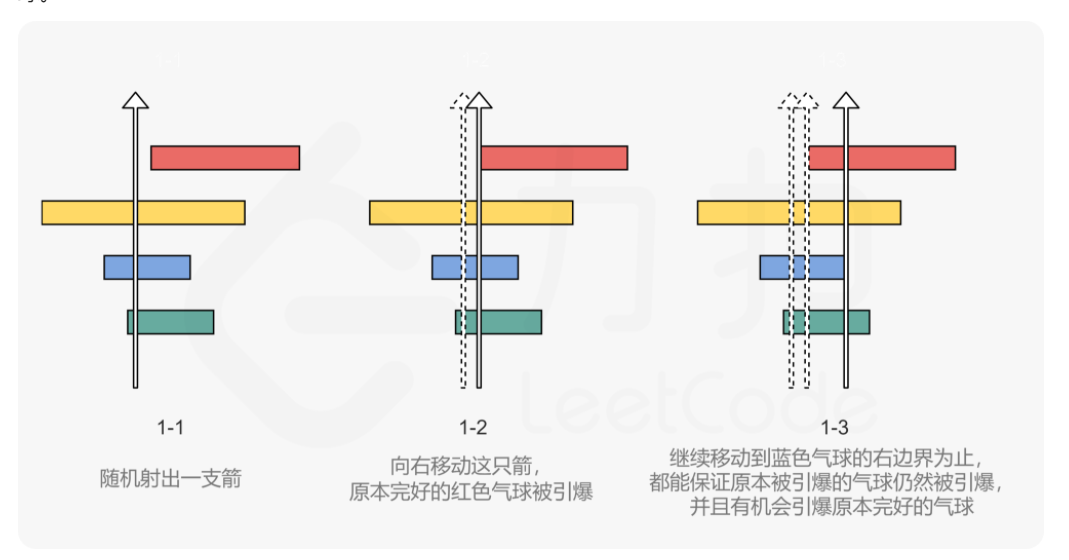
如图 1-1 所示,我们随机射出一支箭,引爆了除红色气球以外的所有气球。我们称所有引爆的气球为「原本引爆的气球」,其余的气球为「原本完好的气球」。可以发现,如果我们将这支箭的射出位置稍微往右移动一点,那么我们就有机会引爆红色气球,如图 1-2 所示。
那么我们最远可以将这支箭往右移动多远呢?我们唯一的要求就是:原本引爆的气球只要仍然被引爆就行了。这样一来,我们找出原本引爆的气球中右边界位置最靠左的那一个,将这支箭的射出位置移动到这个右边界位置,这也是最远可以往右移动到的位置:如图 1-3 所示,只要我们再往右移动一点点,这个气球就无法被引爆了。
所以这里我们只需要把这些气球数组,按照右边界进行排序,然后计算就可以了,代码如下:
public int findMinArrowShots(int[][] points) {
if(points.length==0){
return 0;
}
Arrays.sort(points,(a,b)->{
if(a[1]<b[1]){
return -1;
}
if(a[1]>b[1]){
return 1;
}
return 0;
});
int result=1;
int rightMin=points[0][1];
for(int i=1;i<points.length;i++){
if(points[i][0]>rightMin){
result++;
rightMin=points[i][1];
}
}
return result;
}
总结:
1.相同的需求,好的思路可以令其在应用的时候响应速度提升数倍,这对于用户来说体验感也会好很多,所以还是要加油啊,不能为了写代码而
写代码,我们要写出高效,简洁,可维护性好,扩展性高的代码
2.按照数据大小排序的时候最好直接进行比较,而非进行减法,一方面是速度更快,另一方面是为了防止越界问题。如:最小负数-正数必然是
越界的,返回一个正数,就好导致排序出现错误,要多注意