得分函数:
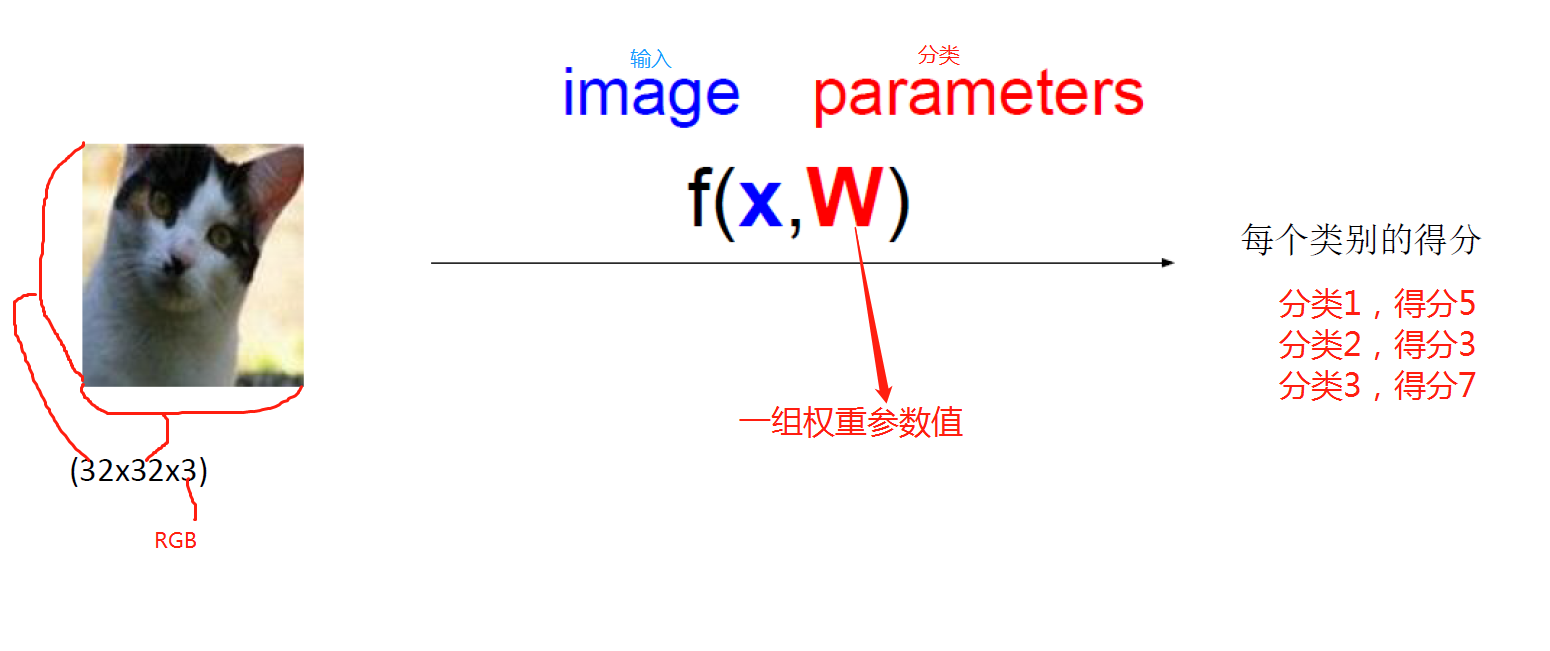
将图片拉伸成一个一维矩阵x,也就是3072×1,最后要得出10个分类的得分值也就是10×1,那w就得是10×3072的矩阵,也就是10组3072个特征的权重值,乘以x,加上b,得到的一个10×1的矩阵,这个矩阵就是最终的每个分类的得分值。
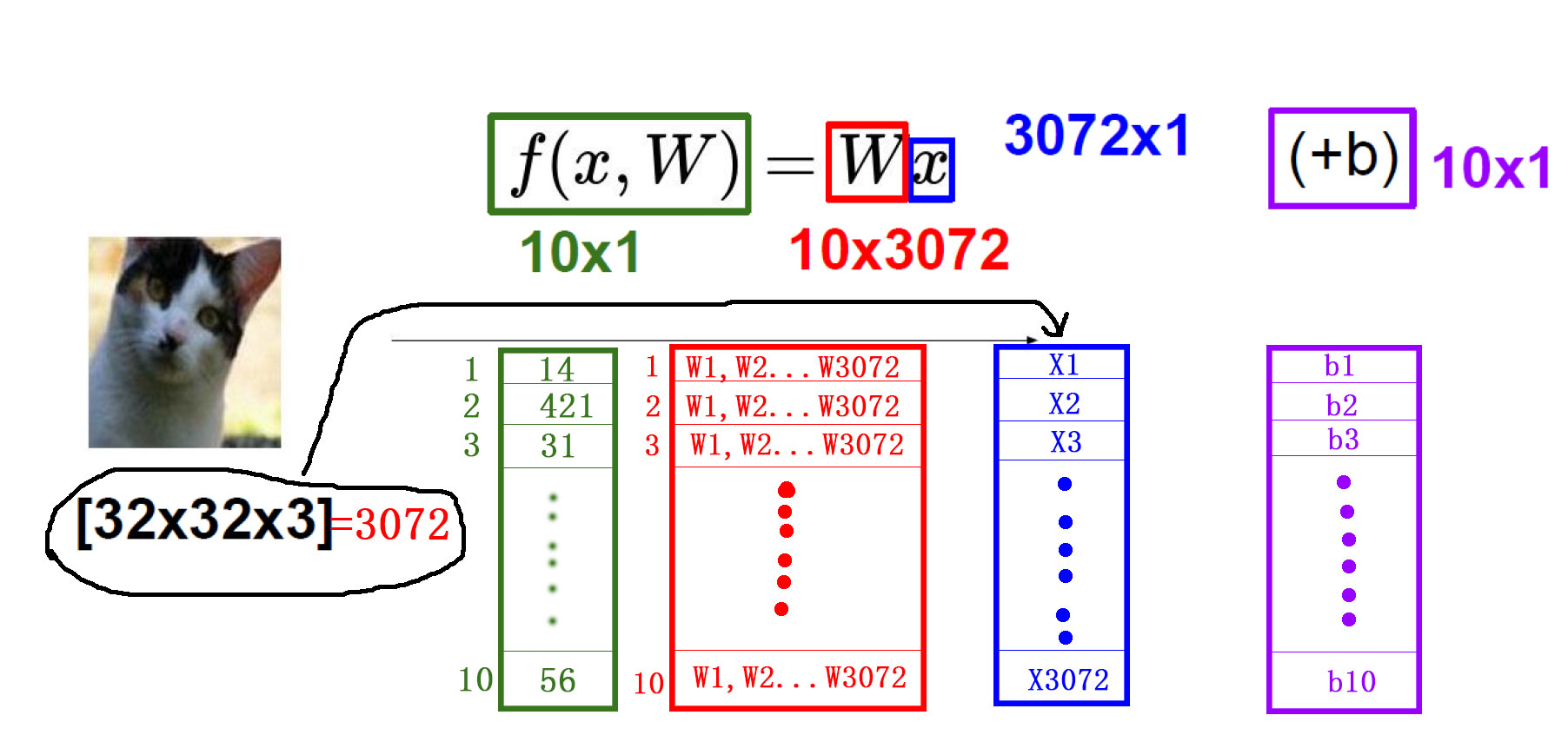
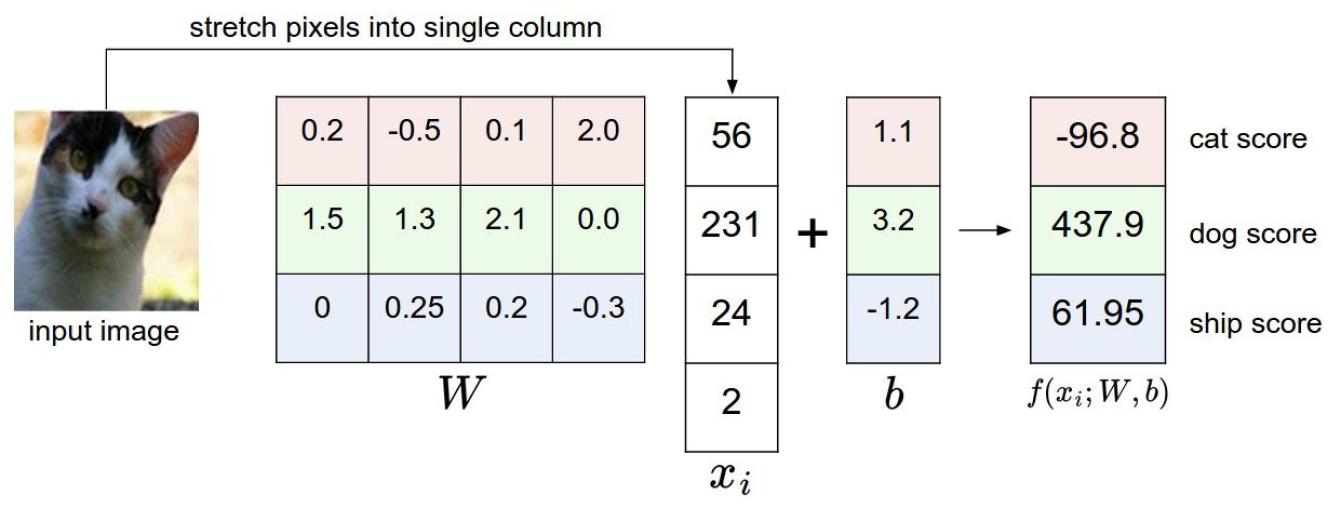
假设将图像分为2×2个像素点,最后又3中类型,那么图像可以被拉伸为4×1的矩阵,最后的结果是3×1的矩阵,那么权重W只能是4×3的矩阵了
也就是说有3组权重参数,每组参数中有4个特征的权重,这里的3组权重参数对应于最后要分类的3个类别,4个特征的权重代表每个特征所占的该类别的重要性(其中负值表示起到了反作用)。
这个例子中,最后得到狗的得分值最高。当然这只是个例子,不代表普遍性。
--------------------------2018年10月14日02:52:49--睡觉---------------------------------------
--------------------------2018年10月14日16:41:09--继续---------------------------------------
相当于做了这么一件事:
利用一个直线作为决策边界,将样本进行分类
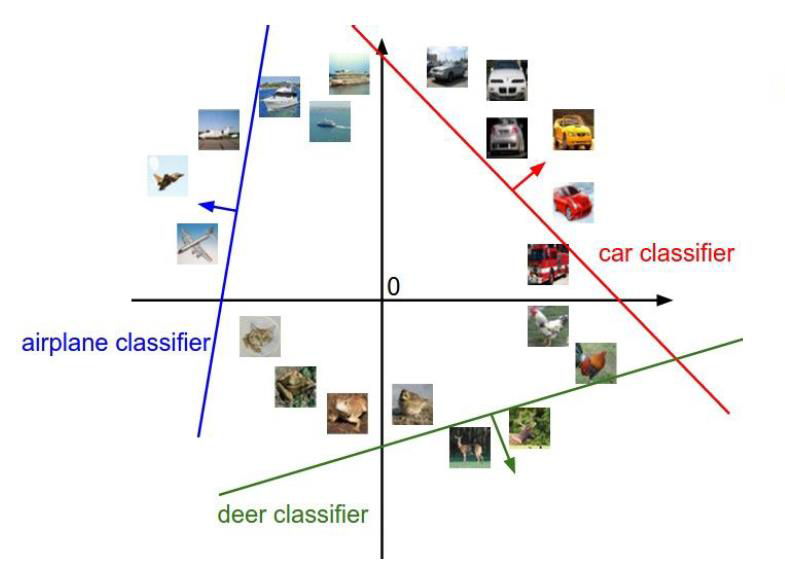
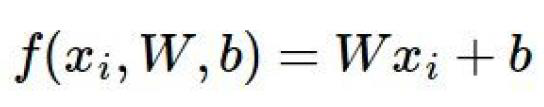
b表示与Y轴的焦点。
损失函数:
![]()

输入猫的图像,输出类别得分,猫:3.2,车5.1,青蛙:-1.7
5.1-3.2表示输入猫判断为车与输入猫判断为猫的得分差异,
再加上1,表示对损失函数的容忍程度,这里的1可以换成任何实数,可以用△表示。
意义在于看看判断错误的情况下,得分与判断正确的情况下的最大差异
通过损失函数可以衡量当前的模型到底是怎么样的。




绿色表示错误的得分值,蓝色表示正确的得分值。
delta表示容忍程度。
如果对于所有样本损失函数是加起来之后在求一个均值。
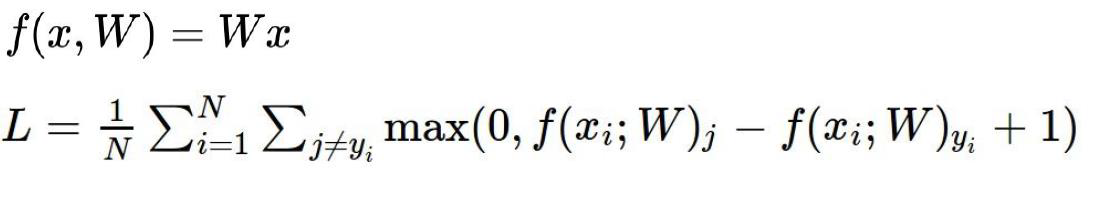
也就是说,样本多少,对于损失函数是没有关系的。
如果有下列一组输入和权重
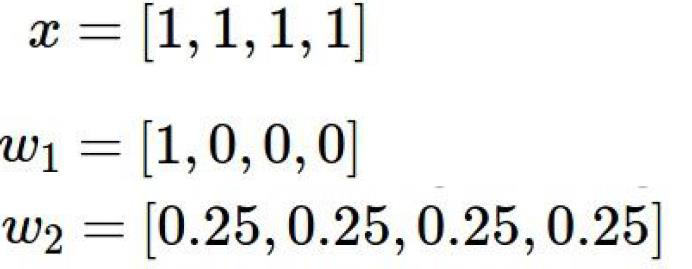
得到的f(x,W)都是1
w1只关注x样本的第一个像素(其他权重都为0),
w2关注的是x样本的所有像素
那么如果新来一个x像素中,第一个像素是一个背景,毫无意义的话,
w1的权重就会判断错误
所以说,我们希望要一个w2模型,而不是要w1模型。
所以我们需要引入一个叫做正则化惩罚项的东西
用来惩罚
正则化惩罚项:
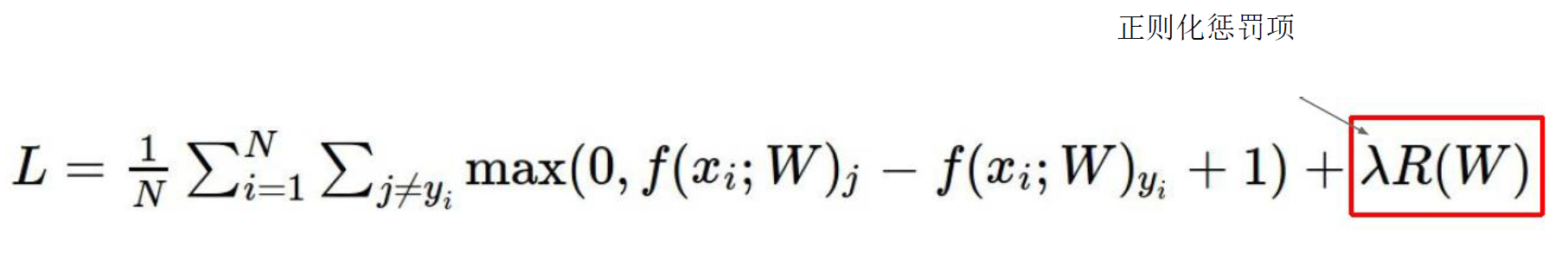
![]()
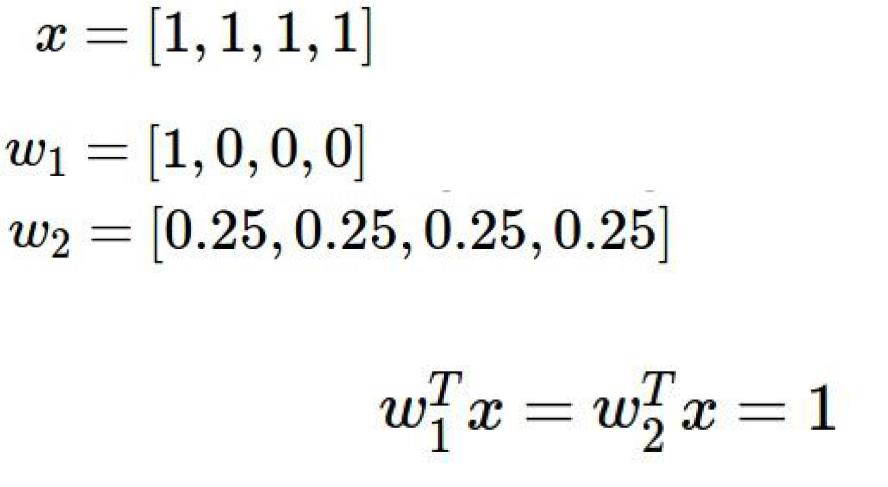
R(W1) = 1+0+0+0 =1
R(w2) = 1/16+1/16+1/16+1/16 = 4/16 = 1/4
说明了对于w1的惩罚力度要大于w2的惩罚力度,所以w1的损失函数就要大于w2的损失函数,
那么就说明模型w1的损失要大于模型w2的损失。
损失函数就可以表示为:
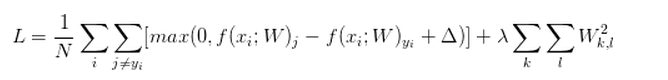
紧接着又有一个问题
我们利用w模型判断出的结果总是得分值,没有概率来的直白,
比如,w判断是猫的得分55,汽车的的得分35,青蛙的得分96,就不如
猫的概率是13%,汽车的概率是32%,青蛙的概率是55%。
如何转换为概率?用softmax分类器,其中
有sigmoid函数来解决实际值转换为概率的问题
softmax分类器
sigmoid函数:
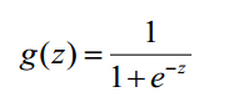

将得分函数映射到sigmoid函数中,然后在通过sigmoid函数得出的概率值进行分类。
Softmax的输出(归一化的分类概率)
损失函数:交叉熵损失(cross-entropy loss)

softmax函数:

其输入值是一个向量,向量中元素为任意实数的评分值
输出一个向量,其中每个元素值在0到1之间,且所有元素之和为1
softmax要做一件什么事?就是将前边所说的得分值映射到e的指数上,然后再计算权重

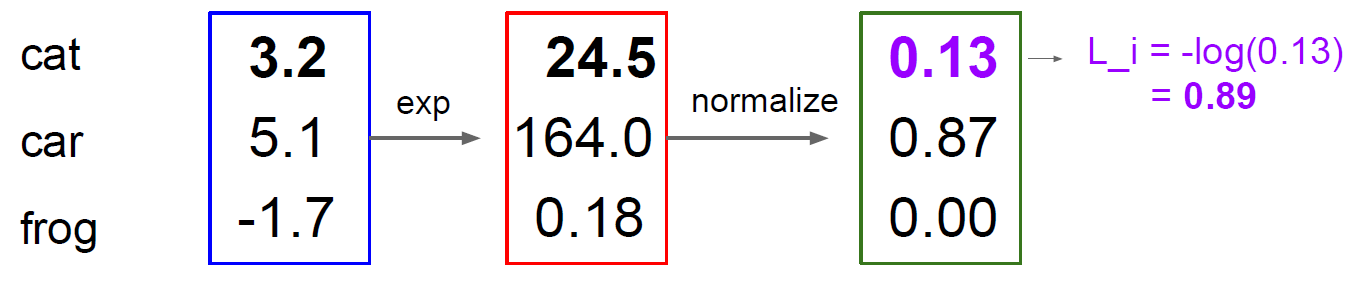
比如这个例子,输入猫,输出猫的得分是3.2,e的3.2次方是24.5,也就是将3.2映射到了e的指数上,
同理5.1映射为164.0;1-.7映射为0.18
这里的exp做的事,相当于softmax函数的分子部分。
然后normalize做的就是归一化的事情了。
24.5÷(24.5+164.0+0.18) =0.13
24.5÷(24.5+164.0+0.18) =0.87
24.5÷(24.5+164.0+0.18) =0.00
这里softmax函数输出的是一个概率值,也就是权重值。
那么softmax的损失函数是什么样的?取对数。
顾名思义,损失函数,
损失值越大就说明误差越大,模型效果越差;
损失值越小就说明误差越小,模型效果越好。
损失函数:交叉熵损失(cross-entropy loss)

只对softmax函数预测正确的概率求损失。
就像上图的0.13,输入一个猫,输出的是是猫的概率为0.13,是汽车的概率是0.87,是青蛙的概率是0.00
那么判断正确的概率是0.13
sofamax的损失函数就只对这个0.13记性求损失函数。
由于对数函数的特性,
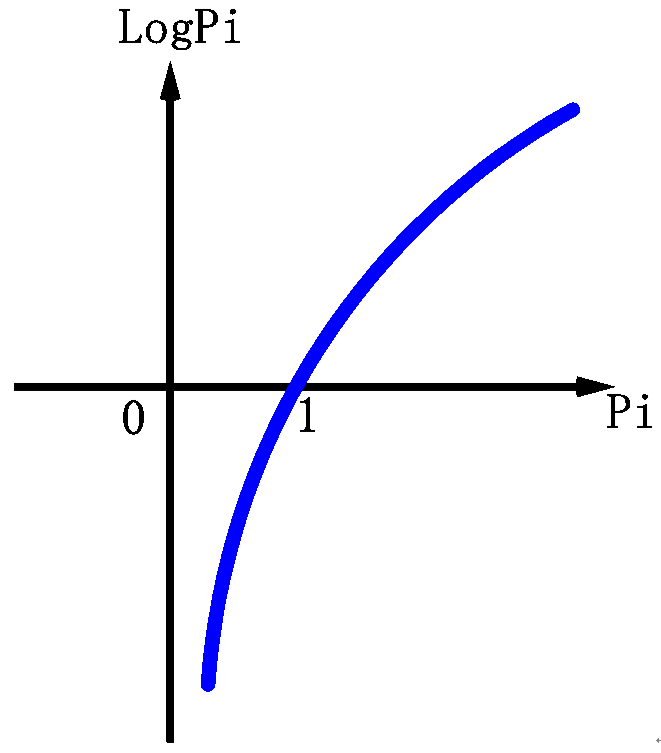
概率(Pi)的取值只是0~1之间
那么概率越大,logPi的值就越接近0,对应于损失函数的意义,正确的概率越大,损失就会越小。
加一个负号的意思就是把损失大的值变为正的。
所以
对0.13取对数加负号,得到的值是0.89
所以这个w模型用softmax函数得出的损失值是0.89
那么问题来了,前边说的得分值,和得分值计算出的损失函数,用的好好的,为什么要多此一举使用softmax函数和它的损失值呢?
举个例子:
如果一个模型输出的分类得分是:10,9,9;10是正确类别
那么利用svm也就是得分值的那种方法,计算损失值:
max(0,9-10+1)+max(0,9-10+1) = 0
利用softmax计算:
exp(10) = 22026.47
exp(9) = 8103.08
归一化:
22026.47÷(22026.47+8103.08+8103.08) = 0.576
-log10(0.576)=0.24
一个是0,一个是0.24
可以看出对于模型的损失,svm和softmax是有区别的。
而且10,9,9对于分类不是那么的明显,相差只有1。
用softmax的损失函数可以更好地判别模型的好坏。