最优化:
包括前向传播和反向传播
前向传播:
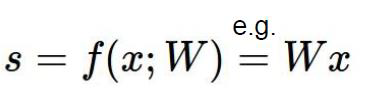
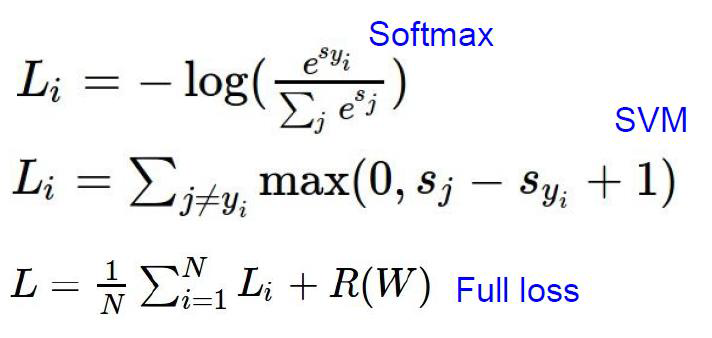
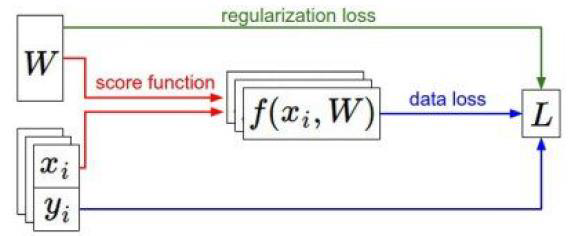
由w和x到损失函数loss的过程叫做前向传播
反向传播:
根据梯度下降的概念,找到最优的w的过程叫做反向传播。
做一件什么事情呢?
根据前向传播的w得到的loss,将loss反馈给上一次前向传播的w进行比较两次的w,看看哪个w使得loss小,那么就用小loss的w。
然后就一直去更新w。就叫做反向传播。
也就相当于回归算法中的参数更新,回归更新的是θ,这里更新的是w,其实都是一样的东西,名字不同而已。
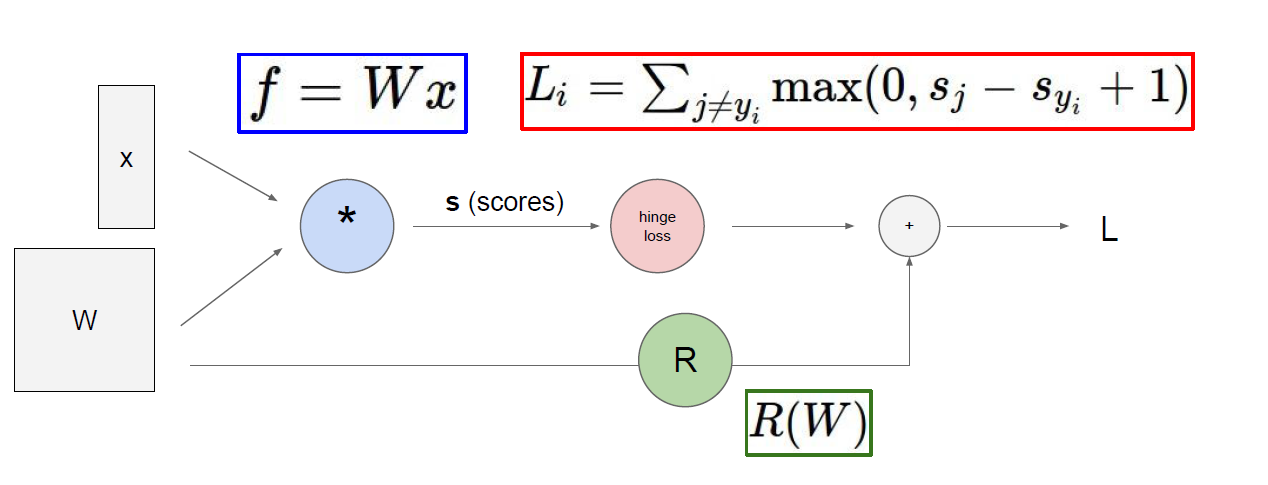
举个例子:
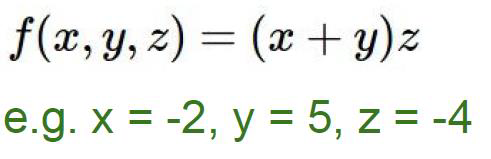
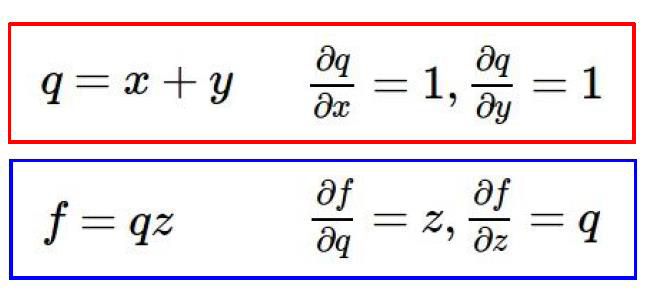
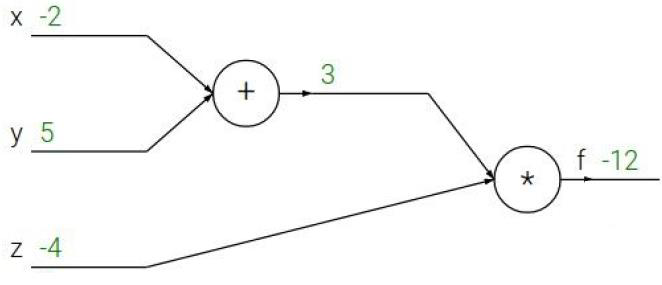
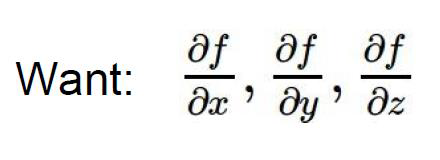
要算x,y,z分别对函数f做了多少贡献,也就是说有多少权重
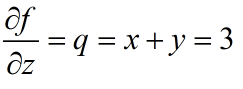
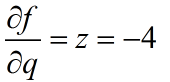
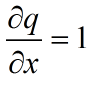
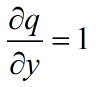
这里存在一个链式法则,也就是说,z对f的权重是3
x对f的权重是-4×1=-4
y对f的权重是-4×1=-4
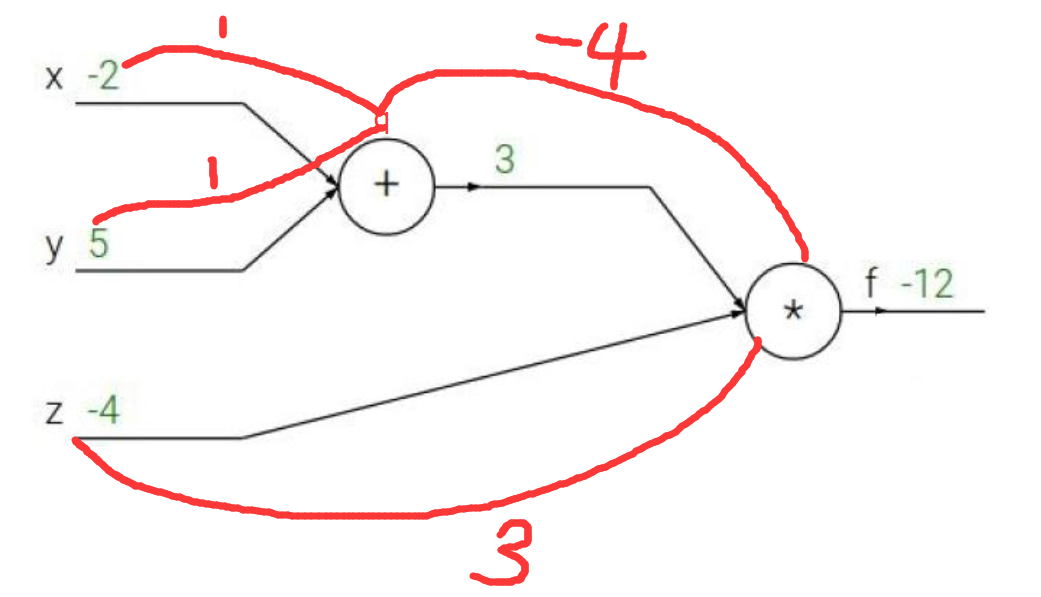
就像下图所示的链式法则,x,y对在L中的权重,分别是L→z→x,和L→z→y两条链所决定的。

再深入一点:
红色代表梯度,绿色代表数值
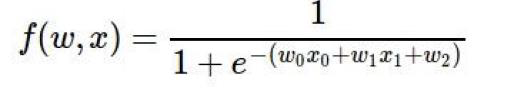
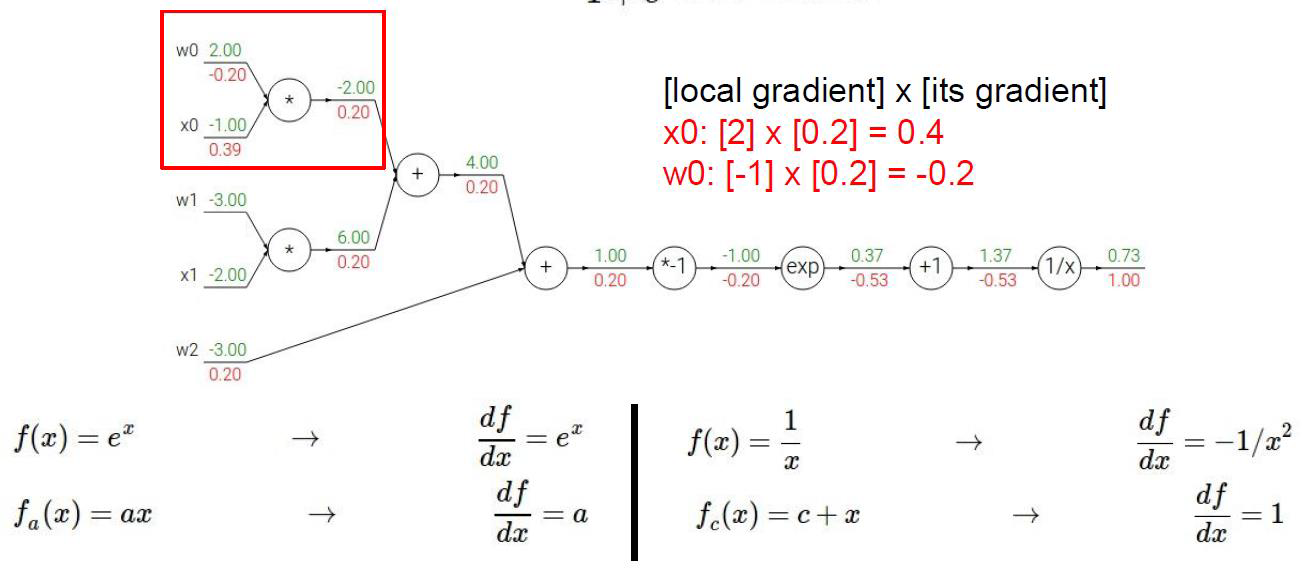
例如最后1.37的1/x函数
梯度是
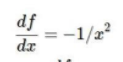
那么这一步的权重就是-1/(0.37*0.37) = 0.53
导数第二步,x+1求导后就是1,所以梯度是1,链式法则求出x+1的权重是1×(-0.53) = -0.53
再看红框里的,假设红框里的韩式是q
那么w0的权根据链式法则就是
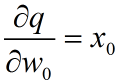
与q的偏导相乘
就是-1×0.2=-0.2
将sigmoid函数合起来之后:
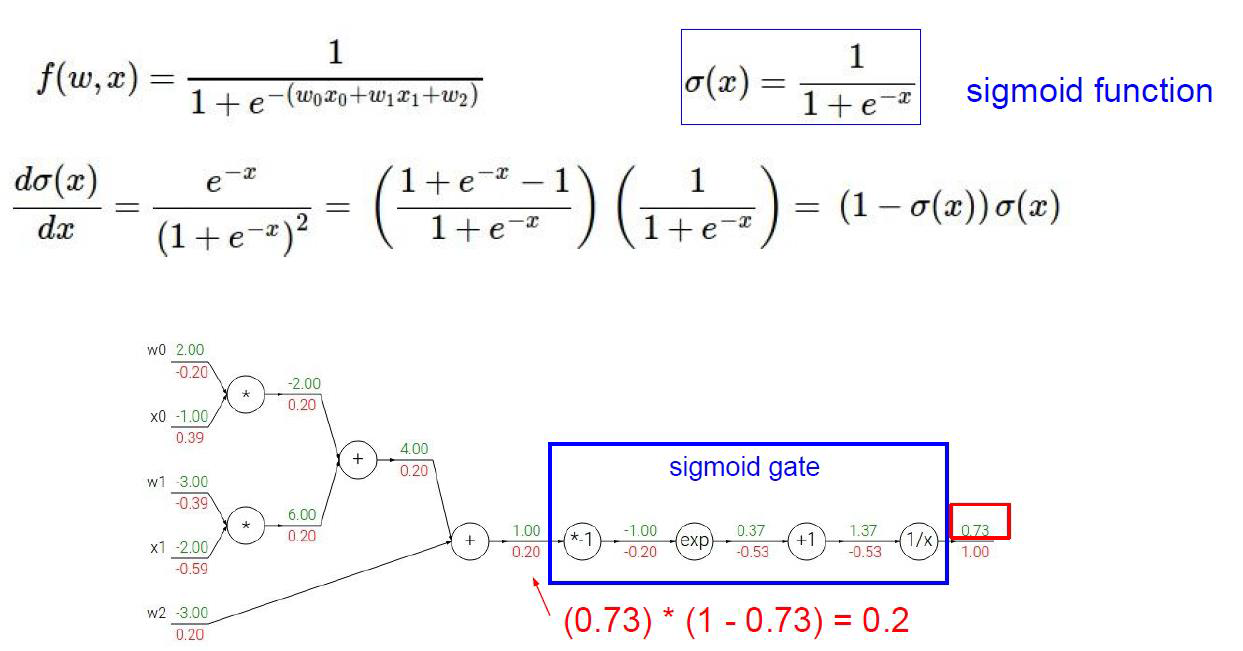
这种做法可以简化流程,如果不是sigmoid函数,而是一个非常负责的函数,可以对整体进行求导而简化流程。
又有一个问题:
链式法则中间的圈圈是干什么的?
这些圈圈叫做门单元。
门单元:

加法门单元:均等分配,导数相同,x+y对x求导是1,对y求导是1
MAX门单元:给最大的,w,z求max操作,最终的结果是z,所以梯度只跟z有关系。
乘法门单元:互换的感觉,导数互换,xy对x的导数是y,xy对y的导数是x