（逆元+快速幂）求组合数

大多数的编程问题都离不开数学问题，而排列组合作为数学的一重要分支，自然也会被列入编程学科里来。

下面给出一道简单例题：

众所周知，不定方程的解有0个或者若干个。
给出方程:

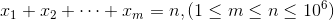
想知道这个不定方程的正整数解和非负整数解各有几个。
（链接：https://ac.nowcoder.com/acm/contest/553/D来源：牛客网）
很容易的，我们通过数学方法能推出正整数解s1=C（m-1,n-1）
非负整数解s2=C(m-1,n+m+1)。
那么我们应该怎样实现它呢？

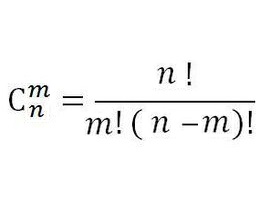
自然而然，我们会想到用阶乘

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#include<queue>

using namespace std;
#define maxn 1000005
#define N 1005
#define INF 0x3f3f3f3f
#define ll long long
#define ld long double
const int mod=1e9+7;

ll m,n;
ld s1=1,s2=1;        //这里必须要用double，因为下面的计算过程中每过一次都有除法运算
int main()
{
    scanf("%lld %lld",&m,&n);
    if(m>n)s1=0;
    if(m==1){
        printf("1 1");
        return 0;
    }
    if(m>1){
        int c=n-m;
        for(int i=n-1;i>m-1;i--){
            s1=s1*i/c;                  //很多人会问为什么要一边累乘一边除去c，到最后在一起计算不行吗？
            c--;                        //如果不除去的话20的阶乘longlong就炸了
        }                               //虽说我这样做也没能让计算位数达到10^6...
        if(m-1>n){
            c=n;
            for(int i=m+n-1;i>m-1;i--){
                s2=s2*i/c;
                c--;
            }
        }
        else{
            c=m-1;
            for(int i=m+n-1;i>n;i--){
                s2=s2*i/c;
                c--;
            }
        }
    }
    printf("%0.Lf %0.Lf",s1,s2);
    return 0;
}

既然直接计算解决不了问题，那我们就把目光转向更高等的数学理论——费马小定理
pow(a,p) ≡ a ( mod p)
这里我们把等式两边同除pow(a,2)
得到的式子就是： pow(a,p-2) ≡ 1/a ( mod p)
∴ 1/a mod p=pow(a,p-2) mod p;
所以上面组合数的分母求余后的值就可以计算了~~~
这里应该会有人有疑问为什么求模要这么麻烦，直接把分母分开来计算，累乘的时候求个模就行了。注意！！！这里是重点！！！除法求模不能类似乘法，对于（A/B）mod C，直接（A mod C）/ （B mod C）是错误的；应该要先将B转换成其逆元b=1/B，之后求出(A*b)modC即可；

话不多说，贴上代码(本蒟蒻也是学习借鉴了一下那些大神的代码）：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#include<queue>

using namespace std;
#define maxn 300005
#define N 1005
#define inf 0x3f3f3f3f
#define LL long long
const int mod=1e9+7;
  
LL pri[maxn];
LL ni[maxn],ans1,ans2;
LL pow(LL a,int b)         //快速幂求逆元时间复杂度为O(logn)
{  
    LL ans=1,base=a;  
    while(b)  
    {  
        if(b&1)  
            ans=(base*ans)%mod;  
        base=(base*base)%mod;  
        b/=2;
    }  
    return ans;  
}  
void s()       //打个表
{  
    pri[0]=1;  
    ni[0]=1;  
    for(int i=1;i<maxn;i++)  
    {
        pri[i]=pri[i-1]*i%mod;
        ni[i]=pow(pri[i],mod-2);  
    }
}
int main()  
{  
    s();
    int n,m;
    scanf("%d %d",&m,&n);  
    ans1=((pri[n-1]*ni[m-1]%mod)*ni[n-m])%mod;
    ans2=((pri[n+m-1]*ni[m-1]%mod)*ni[n])%mod;
    printf("%lld %lld",ans1,ans2);
    return 0;  
}