Forethought Future Cup

You are given a set of nn points in a 2D plane. No three points are collinear.

A pentagram is a set of 55 points A,B,C,D,EA,B,C,D,E that can be arranged as follows.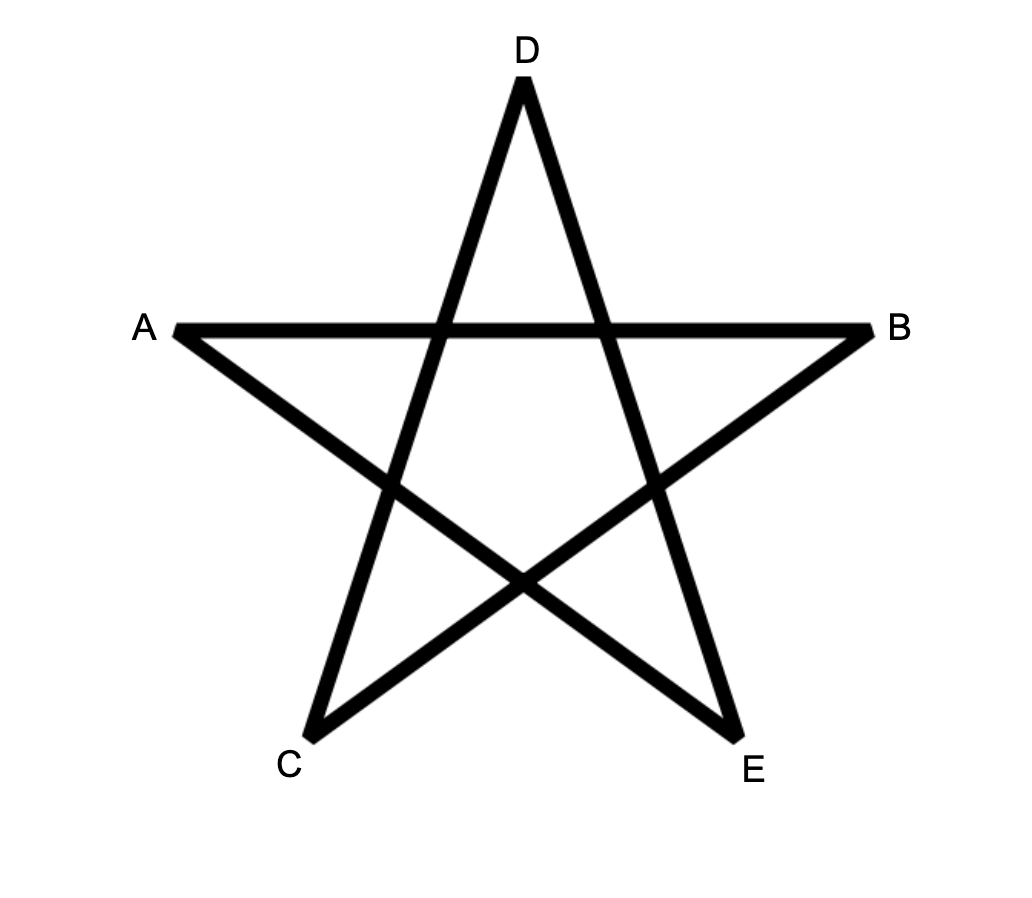Note the length of the line segments don't matter, only that those particular intersections exist.

Count the number of ways to choose 55 points from the given set that form a pentagram.

这道题是一道很简单的计算几何题。

很容易可以发现这道题的目的实际上是要我们求五个点组成的凸包总数。

我们可以设一个f[i][j][k]表示从i点出发，经过k个点到达j点的方案数。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define N 500
#define ll long long
#define db double
using namespace std;
ll n,i,j,k,ans,num,f[N][N][10],x,y;
struct node{
    ll x,y;    
}p[N];
struct line{
    ll a,b;
}lp[N*N];
void insert(ll x,ll y){
    num++;
    lp[num].a=x;
    lp[num].b=y;
}
ll cmp(line x,line y){
    db s1,s2;
    s1=atan2(p[x.b].y-p[x.a].y,p[x.b].x-p[x.a].x);
    s2=atan2(p[y.b].y-p[y.a].y,p[y.b].x-p[y.a].x);
    return s1<s2;
}
int main(){
    scanf("%lld",&n);
    for (i=1;i<=n;i++)
        scanf("%lld%lld",&p[i].x,&p[i].y);
    for (i=1;i<=n;i++)
        for (j=1;j<=n;j++)
            if (i!=j)
                insert(i,j);
    sort(lp+1,lp+num+1,cmp);
    for (i=1;i<=num;i++){
        x=lp[i].a,y=lp[i].b;
        f[x][y][1]=1;
        for (j=1;j<=n;j++)
            for (k=1;k<5;k++)
                f[j][y][k+1]+=f[j][x][k];
    }
    for (i=1;i<=n;i++)
        ans+=f[i][i][5];
    printf("%lld
",ans);
    return 0;
}