深度学习03--神经网络

神经网络

简介

人工神经网络（ Artificial Neural Network，简写为ANN）也简称为神经网络(NN)。是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）结构和功能的计算模型。经典的神经网络结构包含三个层次的神经网络。分别为输入层，输出层以及隐藏层。

其中每层的圆圈代表一个神经元，隐藏层和输出层的神经元有输入的数据计算后输出，输入层的神经元只是输入

特点

• 每个连接都有个权值
• 同一层神经元之间没有连接
• 最后的输出结果对应的层也称之为全连接层

感知器

感知机就是模拟这样的大脑神经网络处理数据的过程。

组成部分

• 输入权值，一个感知器可以有多个输入x1,x2,x3...x​n​​,每个输入上有一个权值w​i​​
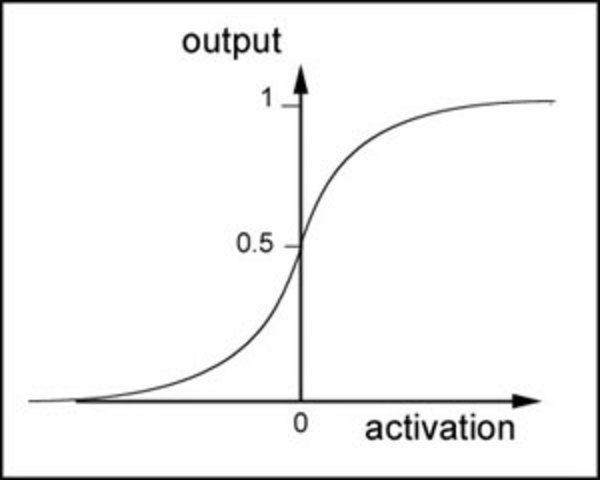
• 激活函数，感知器的激活函数有许多选择，以前用的是阶跃函数，sigmoid(1/(1+e^(w*x)​​)),其中z为权重数据积之和
• 输出，y=f(w*x+b)

感知机是一种最基础的分类模型，类似于逻辑回归，不同的是，感知机的激活函数用的是sign，而逻辑回归用的sigmoid。感知机也具有连接的权重和偏置

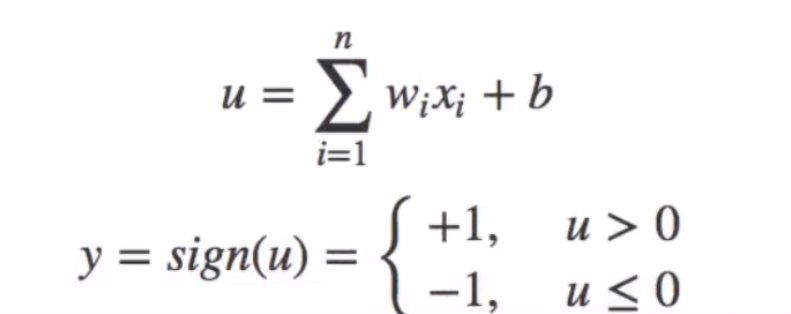
神经网络解释

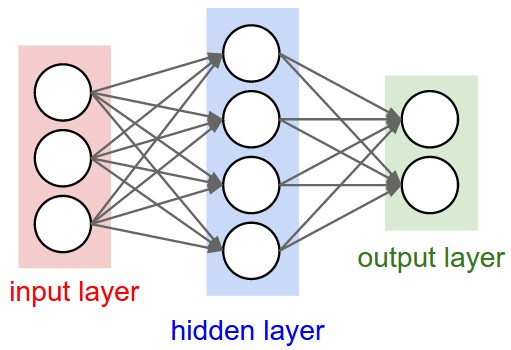
神经网络其实就是按照一定规则连接起来的多个神经元。

• 输入向量的维度和输入层神经元个数相同
• 第N层的神经元与第N-1层的所有神经元连接，也叫 全连接
• 上图网络中最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，可以有多个输出层。我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
• 而且同一层的神经元之间没有连接
• 并且每个连接都有一个权值

那么我们以下面的例子来看一看，图上已经标注了各种输入、权重信息。

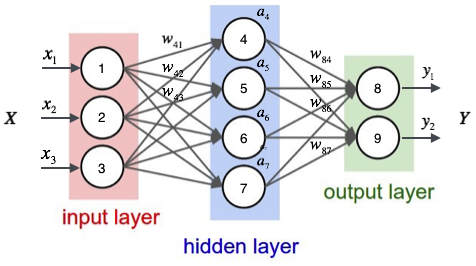
 对于每一个样本来说，我们可以得到输入值

x_1,x_2x​1​​,x​2​​,x​3​​,也就是节点1，2，3的输入值，那么对于隐层每一个神经元来说都对应有一个偏置项bb，它和权重一起才是一个完整的线性组合

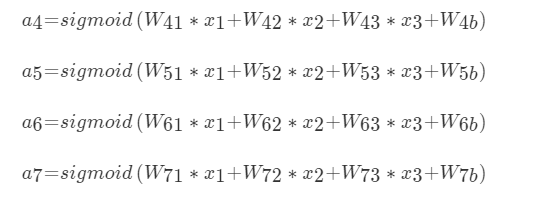
 这样得出隐层的输出，也就是输出层的输入值.

矩阵表示

 同样，对于输出层来说我们已经得到了隐层的值，可以通过同样的操作得到输出层的值。那么重要的一点是，分类问题的类别个数决定了你的输出层的神经元个数

原理

神经网络解决多分类问题最常用的方法是设置n个输出节点，其中n为类别的个数。

任意事件发生的概率都在0和1之间，且总有某一个事件发生（概率的和为1)。如果将分类问题中“一个样例属于某一个类别"看成一个概率事件，那么训练数据的正确答案就符合一个概率分布。如何将神经网络前向传播得到的结果也变成概率分布呢? Softmax回归就是一个非常常用的方法。

softmax回归

softmax回归有两个步骤：首先我们将我们的输入的证据加在某些类中，然后将该证据转换成概率。每个输出的概率，对应着one -hot编码中具体的类别。

 

 

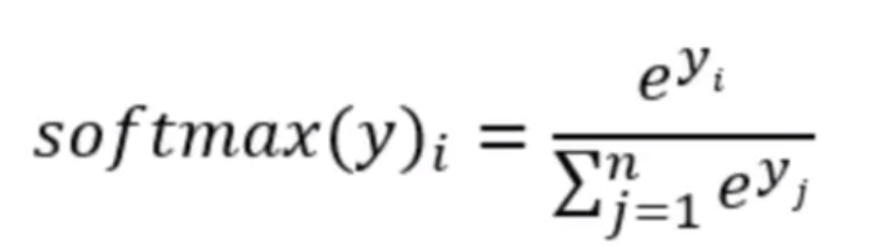
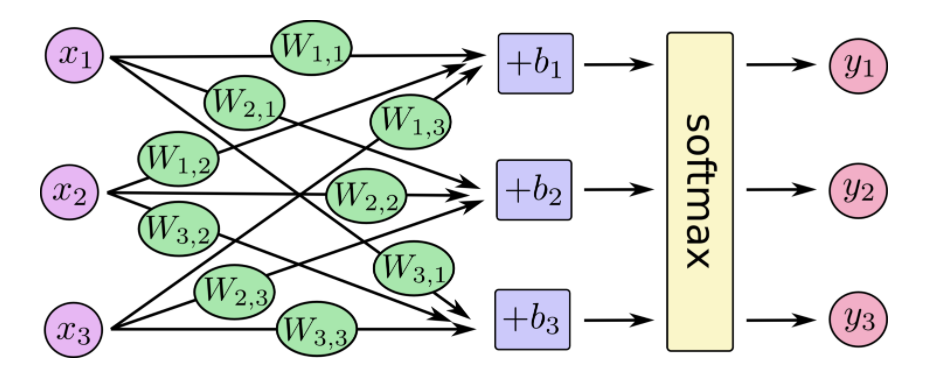
也就是最后的softmax模型，用数学式子表示：y=softmax(Wx+b)

交叉熵损失

它表示的是目标标签值与经过权值求和过后的对应类别输出值

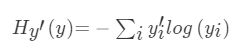
损失计算

提高对应目标值为1的位置输出概率大小

损失大小

神经网络最后的损失为平均每个样本的损失大小

• 对所有样本的损失求和取其平均值

softmax、交叉嫡损失API

 

准确率计算

1. 比较输出的结果最大值所在位置和真实值的最大值所在位置，然后转换为0  1格式
2. 求平均

    #  argmax(y_true, axis=1)求矩阵行最大值的索引  cast()类型转换
    bool_list = tf.equal(tf.argmax(y_true, axis=1), tf.argmax(y_predict, axis=1))
    accuracy = tf.reduce_mean(tf.cast(bool_list, tf.float32))

案例：Mnist手写数字识别

代码

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data


def full_connection():
    tf.compat.v1.disable_eager_execution()
    """
    用全连接对手写数字进行识别
    :return:
    """
    # 1）准备数据
    mnist = input_data.read_data_sets("../mnist_data", one_hot=True)
    # 用占位符定义真实数据
    X = tf.compat.v1.placeholder(dtype=tf.float32, shape=[None, 784])
    y_true = tf.compat.v1.placeholder(dtype=tf.float32, shape=[None, 10])

    # 2）构造模型 - 全连接
    # [None, 784] * W[784, 10] + Bias = [None, 10]
    weights = tf.Variable(initial_value=tf.compat.v1.random_normal(shape=[784, 10], stddev=0.01))
    bias = tf.Variable(initial_value=tf.compat.v1.random_normal(shape=[10], stddev=0.1))
    y_predict = tf.matmul(X, weights) + bias

    # 3）构造损失函数
    loss_list = tf.nn.softmax_cross_entropy_with_logits(logits=y_predict, labels=y_true)
    loss = tf.reduce_mean(loss_list)

    # 4）优化损失
    # optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)
    optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=0.01).minimize(loss)

    # 5）增加准确率计算
    bool_list = tf.equal(tf.argmax(y_true, axis=1), tf.argmax(y_predict, axis=1))
    accuracy = tf.reduce_mean(tf.cast(bool_list, tf.float32))

    # 初始化变量
    init = tf.compat.v1.global_variables_initializer()

    # 开启会话
    with tf.compat.v1.Session() as sess:

        # 初始化变量
        sess.run(init)

        # 开始训练
        for i in range(5000):
            # 获取真实值
            image, label = mnist.train.next_batch(500)

            _, loss_value, accuracy_value = sess.run([optimizer, loss, accuracy], feed_dict={X: image, y_true: label})

            print("第%d次的损失为%f，准确率为%f" % (i+1, loss_value, accuracy_value))


    return None

if __name__ == "__main__":
    full_connection()