欧拉函数Φ(x)是小于等于x的正整数中与x互质的数的个数。
先放一下公式:
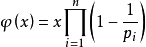
然后放一下代码:
1 inline int totient(int x) { 2 int tot = x; 3 for (int i = 2; i * i <= x; ++i) 4 if (x % i == 0) { 5 tot = tot / i * (i - 1); //先做除法防溢出 6 while (x % i == 0) x /= i; //将此质因数完全除尽 7 } 8 if (x > 1) tot = tot / x * (x - 1); //最后可能剩个质数,或一开始就是个质数 9 return tot; 10 }
实际上上述代码用于求少量数的欧拉函数还是可以的,但如果需要求一段较长区间内的欧拉函数值时,我们可以用下面的方法。
1 int phi[maxn]; 2 3 inline void getphi(int n) { 4 for (int i = 1; i <= n; ++i) phi[i] = i; 5 for (int i = 2; i <= n; ++i) //找出质数,处理他们的整数倍 6 if (phi[i] == i) for (int j = i; j <= n; j += i) 7 phi[j] = phi[j] / i * (i - 1); //还是公式 8 }