CNN学习笔记:全连接层
全连接层
全连接层在整个网络卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的特征表示映射到样本的标记空间的作用。
一段来自知乎的通俗理解:
从卷积网络谈起,卷积网络在形式上有一点点像咱们正在召开的“人民代表大会”。卷积核的个数相当于候选人,图像中不同的特征会激活不同的“候选人”(卷积核)。池化层(仅指最大池化)起着类似于“合票”的作用,不同特征在对不同的“候选人”有着各自的喜好。
全连接相当于是“代表普选”。所有被各个区域选出的代表,对最终结果进行“投票”,全连接保证了receiptive field 是整个图像,既图像中各个部分(所谓所有代表),都有对最终结果影响的权利。
在实际使用中,全连接层可由卷积操作实现:对前层是全连接的全连接层可以转换为卷积核为1*1的卷积;而前层是卷积层的全连接层可以转换为卷积核为前层卷积输出结果的高和宽一样大小的全局卷积。
全连接层实现原理
在卷积神经网络的最后,往往会出现一两层全连接层,全连接一般会把卷积输出的二维特征图转化成一维的一个向量,这是怎么来的呢?目的何在呢?
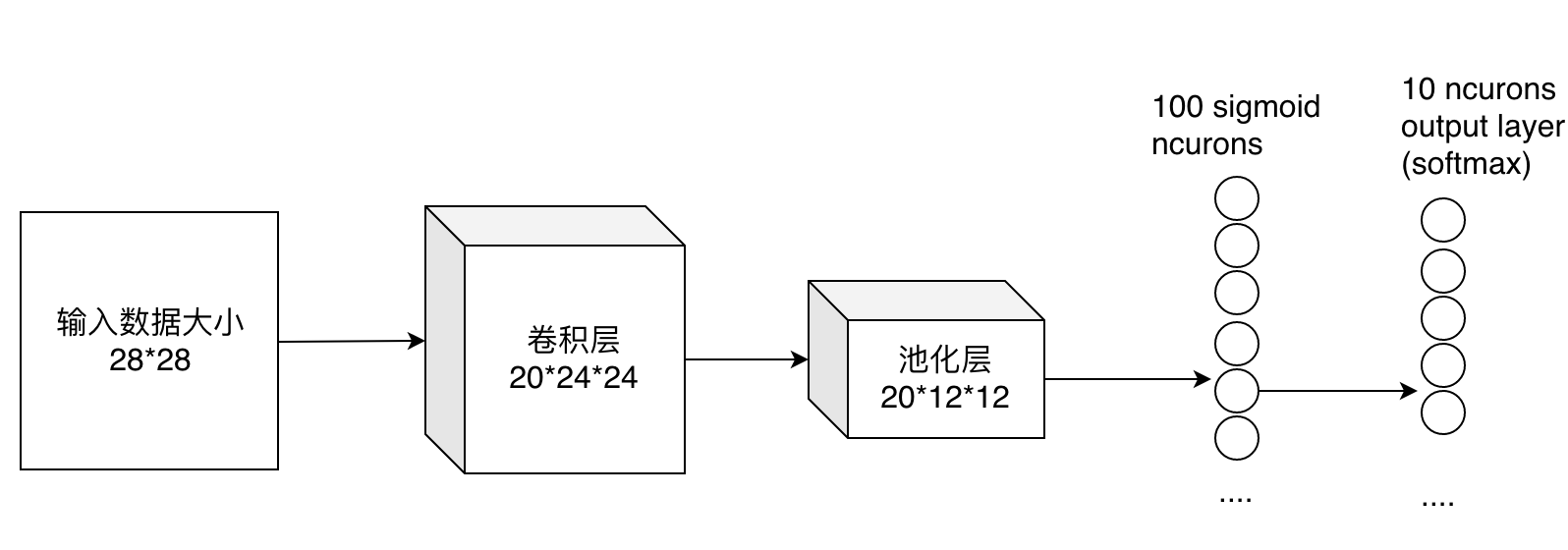
最后的两列小圆球就是两个全连接层,在最后一层卷积结束后,进行了最后一次池化,输出了20个12*12的图像,然后通过了一个全连接层变成了1*100的向量。
这是怎么做到的呢,其实就是有20*100个12*12的不同卷积核卷积出来的,我们也可以这样想,就是每个神经元的输出是12*12*20个输入值与对应的权值乘积的和。对于输入的每一张图,用了一个和图像一样大小的核卷积,这样整幅图就变成了一个数了,如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。