LeetCode：为运算表达式设置优先级【241】

LeetCode：为运算表达式设置优先级【241】

题目描述

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。

示例 1:

输入: "2-1-1"
输出: [0, 2]
解释: 
((2-1)-1) = 0 
(2-(1-1)) = 2

示例 2:

输入: "2*3-4*5"
输出: [-34, -14, -10, -10, 10]
解释: 
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

题目分析

　　这道题的核心概念是找一个位置去分割表达式，但是这里的位置只能是操作符（+、-、*），把原来的表达式分割成为两个子表达式，先分别求解两个子表达式的值，接着子表达式递归求解出来的值的集合根据操作符做笛卡尔积。

　　例如：

　　　　

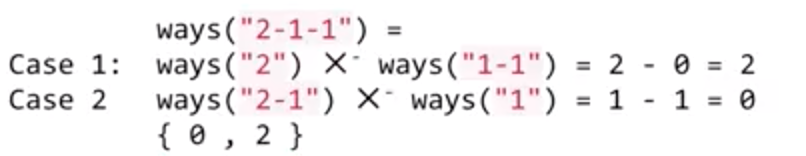
　　例如：

　　

　　这道题真的应该反思一下，题目中体现的使用括号来实现优先级，但是其实呢，他其实就是考虑了所有的可能性，就跟全排列一样，要求的就是所有结果值。我们使用分治思想，围绕运算符一层一层向下做分割，分割到最后其实就是一个个具体的值，然后在向上左笛卡尔积，并把所有的取值加入到结果中来。

Java题解

 class Solution {
        public List<Integer> diffWaysToCompute(String input) {
           List<Integer> res = new ArrayList<>();
            for(int i = 0;i<input.length();i++)
            {
                char c = input.charAt(i);
                if(c=='+'||c=='-'||c=='*')
                {
                    String partLeft = input.substring(0,i);
                    String partRight = input.substring(i+1);
                    List<Integer> resLeft = diffWaysToCompute(partLeft);
                    List<Integer> resRight = diffWaysToCompute(partRight);
                    for(Integer intLeft:resLeft)
                        for(Integer intRight:resRight)
                        {
                            if(c=='+')
                                res.add(intLeft+intRight);
                            if(c=='-')
                                res.add(intLeft-intRight);
                            if(c=='*')
                                res.add(intLeft*intRight);
                        }
                }
            }
           if(res.size()==0)
               res.add(Integer.valueOf(input));
            return res;
        }
}