1.简介
拉格朗日乘子法,是寻找多元函数在一组约束(可以是等式约束也可以是不等式约束)下的极值
的方法。通过引入拉格朗日乘子,将d个变量与k的约束条件的有约束优化问题转化为d+k个变量的无
约束优化问题。
2.无约束优化
在无约束优化问题中,如果一个函数是凸函数,那么总能通过求偏导等于0的方法求得函数的全局
极小值点。如果不是凸函数,可能会陷入局部极小值点
3.等式约束的优化问题
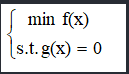
在这里我们优化一个等式约束的问题,假设
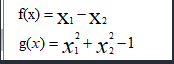
则可以在下图中将这两个函数图像表示出来,其中圆表示等式约束条件,
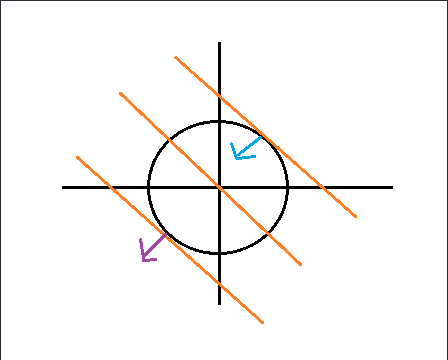
f(x)的梯度为(1,1),g(x)的梯度为半径向外方向,不难看出有以下结论:
- 对于约束平面上的点(在本例中就是圆上的点),其梯度方向正交于约束平面。
- 对于目标函数上的点,其在约束条件下取极值时,其梯度方向也正交于约束平面(图中蓝色所标出的箭头)
从上面的例子中可以看出在等式约束的优化问题中,取最优点时,其目标函数的梯度和约束条件的梯度方向保持相同或者相反。
即
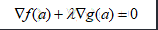
上式中a为最优点,lambda为拉格朗日乘子
所以上述的等式约束条件下的优化问题可以写成下面的拉格朗日函数:
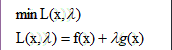
因为上述拉格朗日函数的最小值和原约束条件下的优化函数具有同等的最优点,所以就将原等式约束下的优化问题转换为无约束条件的优化问题。
这样就可以简单的分别对x和lambda求偏导为0时函数的值,从而得到最优值(凸函数)。
4.不等式约束条件
还是上述的例子,而改为g(x)<=0

这次约束条件所取点的范围在整个圆的内部,包括边界。
我们分两种情况来讨论:
- 第一种情况为g(x)<0
也就是说找到的最优点(如果这种情况存在的话)在圆的内部,这种情况下这个约束条件是没用的,应为落在内部的最优点完全可以通过对目标函数求偏导=0就可以确定。只有当目标在约束条件所确定的平面之外时,才会试着突破约束去达到目标,这时候约束条件才能起到约束的作用。
- 第二种情况g(x)=0
这种情况就是等式约束条件中所说的情况。不过值得注意的一点是,这时拉格朗日乘子lambda为正数,可以这么想象:因为目标在约束平面之外,目标函数的梯度不断的“拉扯”点往外走,约束条件为使得这个点不能突破约束,其梯度就“拉扯”着点往内走,梯度提供了点运动的力。当点稳定时,作用在点上的力,作用在同一直线上且方向相反。
因此就得出了Karush-Kuhn-Tucker(KKT)条件
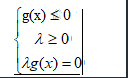
下面对上式解释:
KKT条件的第一式:原来的约束条件
KKT条件的第二式:lambda>=0就是上面说的两个力方向相反,即梯度的方向相反
KKT条件的第三式:若最优点在约束平面内部,则lambda=0,约束条件无用
若最优点在约束平面的边界,g(x)=0
5.推广到多个约束
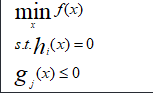
可以转换为:
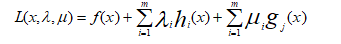
须满足的KKT条件为:
