百度百科关于LCA的解释:LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。(有多种变型例如求两点间的距离如HDU2586,求最大公共的长度如CodeForces - 832D 等等)
题目: POJ 1984 HDU 2586 ZOJ 3195 POJ 1330 CodeForces - 832D
1.跳跃法/倍增LCA优化(在线算法)
倍增练习题:CodeForces - 932D (非LCA)
假设我们求两节点的LCA,需要进行以下几种操作:
1.优先处理出各个节点的深度;
2.判断两节点的深度是否相同;
3.如果不相同,对深度大的节点进行跳跃操作,直到两点深度相同;
4.判断当前两节点所在的节点是否为同一节点,是则其为LCA,否则继续操作5;
5.判断两个节点是否具有相同父亲节点,是则父亲节点为LCA,否则继续操作6;
6.两个节点同时跳相同长度(但是两个节点不能跳到同一个节点去)回至操作5.
假设我们求5和6的LCA,那么我们需要先将5从depth:3开始起跳,一步一步向上跳,直到从5跳到2(即与6相同深度)因为2和6有同一个父亲节点所以1就是5和6的LCA。
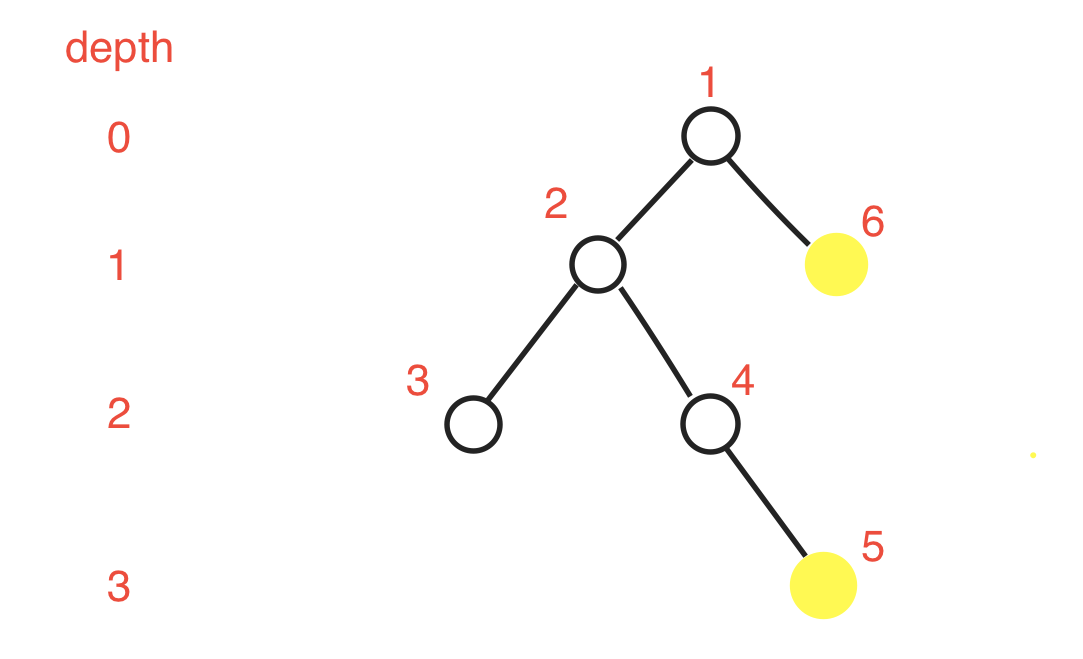
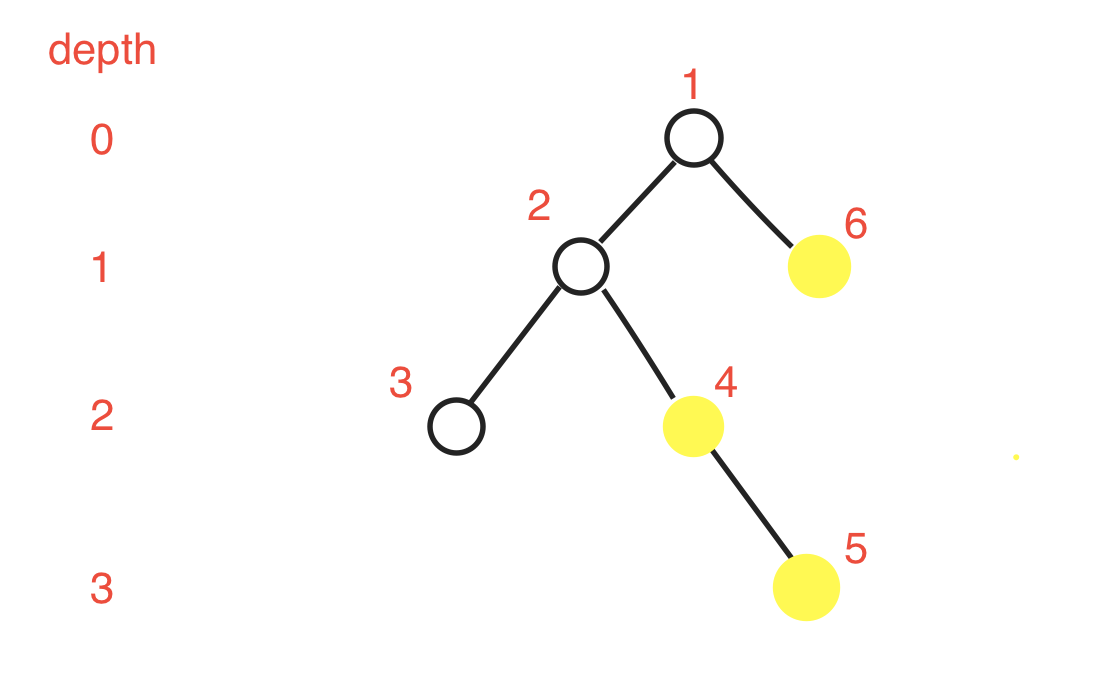

看完这几张图你可能认为这个认为这个算法太简单了(比如说当初不管数据范围的我)只要疯狂向上一格一格跳就好了,dfs一遍就能跑出来了。但是一个一个跳这不会T嘛?因此出现了倍增!!!!什么是倍增?表面理解就是按照倍数增大,计算机的基础是什么?0和1!!!就是二进制!我们可以用二进制来表示所有的数。对于每一个节点我们只要知道其2^j层的祖先是谁,就能让任意一个节点从自身以logn的速度快速跳跃到1.另赋超生动形象的倍增讲解:http://blog.csdn.net/jarjingx/article/details/8180560
核心代码:
//father[][]第一维是表示节点,第二维表示节点的第i个祖先。 //n是节点个数,Logn是根号n(取整) for(int i=1;i<=Logn;i++) father[u][i]=father[father[u][i-1]][i-1];
练手模版题传送门:POJ 1330
详细代码(模版含解释):
关于下面这篇代码处理入度的问题:题目中给出了父亲与儿子的关系所以要进行入度处理,不能随意dfs

#include <cstdio> const int N=1e4+5; using namespace std; int fa[N][14]; int dep[N]; int head[N]; int nx[N]; int to[N]; int tot=1; bool vis[N]; int in[N]; int L,R; void add(int u,int v){//链式前向星存图 to[tot]=v; nx[tot]=head[u]; head[u]=tot++; } void init(int n){//初始化 for(int i=0;i<=n;i++)fa[i][0]=0,in[i]=0,vis[i]=0,head[i]=0,dep[i]=0; tot=1; } void dfs(int u,int d){//dfs处理深度,处理2^j的祖先关系 vis[u]=1; dep[u]=d; for(int i=1;i<14;i++)fa[u][i]=fa[fa[u][i-1]][i-1]; for(int i=head[u];i;i=nx[i]){ int v=to[i]; if(!vis[v])dfs(v,d+1); } } int LCA(int u,int v){ if(dep[u]<dep[v])swap(u,v);//保证u是深度大的那个节点 int d=dep[u]-dep[v];//深度之差 for(int i=0;(1<<i)<=d;i++){//(1<<i)<=d是为了让u在保证不会跳过v的情况下进行跳跃 if((1<<i)&d){ //(1<<i)&d其实就是转化二进制问那几个点可以跳跃 u=fa[u][i];//例如差为5(101)只要在i==0和i==2的情况下跳跃(如果还是不懂就模拟一下) } } if(u==v)return u;//如果两个节点直接相等那么就如操作4所说,该点就是LCA,否则继续进行相同长度的跳跃 for(int i=13;i>=0;i--){ if(fa[v][i]!=fa[u][i]){ u=fa[u][i]; v=fa[v][i]; } } return fa[u][0]; } int main(){ int t; scanf("%d",&t); while(t--){ tot=1; int n; scanf("%d",&n); init(n); for(int i=1;i<n;i++){ int l,r; scanf("%d %d",&l,&r); add(l,r); fa[r][0]=l; in[r]++;//处理入度 } scanf("%d%d",&L,&R); for(int i=1;i<=n;i++) if(!in[i]){ dfs(i,0);//必须从入度为0的点开始dfs break; } printf("%d ",LCA(L,R)); } }

#include<iostream> #include<cmath> #include<algorithm> #include<cstring> #include<cstdio> #include<queue> #include<functional> #include<map> #include<set> #define se second #define fi first #define ll long long #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define Pii pair<int,int> #define pb push_back #define ull unsigned long long #define fio ios::sync_with_stdio(false);cin.tie(0) const double Pi=3.14159265; const double e=2.71828182; const int N=2e5+5; const ull base=163; using namespace std; int head[N]; int to[N]; int nx[N]; int tot=1; int in[N]; int fa[N][20]; int dep[N]; bool vis[N]; void add(int u,int v){ to[tot]=v; nx[tot]=head[u]; head[u]=tot++; } void dfs(int u,int d){ vis[u]=1; dep[u]=d; for(int i=1;i<20;i++){ fa[u][i]=fa[fa[u][i-1]][i-1]; } for(int i=head[u];i;i=nx[i]){ int v=to[i]; if(!vis[v]){ fa[v][0]=u; dfs(v,d+1); } } } int LCA(int u,int v){ if(dep[u]<dep[v])swap(u,v); int d=dep[u]-dep[v]; for(int i=0;(1<<i)<=d;i++){ if((1<<i)&d){ u=fa[u][i]; } } if(u==v)return u; for(int i=19;i>=0;i--){ if(fa[u][i]!=fa[v][i]&&fa[u][i]!=0&&fa[v][i]!=0){ u=fa[u][i]; v=fa[v][i]; } } return fa[u][0]; } int main(){ fio; int n,q; cin>>n>>q; for(int u=2;u<=n;u++){ int v; cin>>v; add(u,v); add(v,u); } dfs(1,0); while(q--){ int a,b,c; cin>>a>>b>>c; int ac=LCA(a,c); int ab=LCA(a,b); int bc=LCA(b,c); int d1=(dep[a]-dep[ac]+dep[c]-dep[ac]+dep[b]-dep[bc]+dep[c]-dep[bc]-(dep[a]-dep[ab]+dep[b]-dep[ab]))/2; int d2=(dep[a]-dep[ab]+dep[b]-dep[ab]+dep[b]-dep[bc]+dep[c]-dep[bc]-(dep[a]-dep[ac]+dep[c]-dep[ac]))/2; int d3=(dep[a]-dep[ab]+dep[b]-dep[ab]+dep[a]-dep[ac]+dep[c]-dep[ac]-(dep[b]-dep[bc]+dep[c]-dep[bc]))/2; cout<<max(d1,max(d2,d3))+1<<endl; } return 0; }
2.Tarjan算法(离线算法)
还是POJ 1330
先附上代码:

#include <cstdio> const int N=1e4+5; using namespace std; int fa[N]; int dep[N]; int head[N]; int nx[N]; int to[N]; int tot=1; bool vis[N]; int in[N]; int L,R; void add(int u,int v){ to[tot]=v; nx[tot]=head[u]; head[u]=tot++; } int find(int x){ return fa[x]==x?x:fa[x]=find(fa[x]); } void tarjan(int u){ vis[u]=1; for(int i=head[u];i;i=nx[i]){ int v=to[i]; if(!vis[v]){ tarjan(v);//不停的向下走直到再往下就没有子节点 fa[v]=u;//更新每个节点的父亲 } } if(u==L){//如果u是需要查询两节点的任意一个节点,就要判断另一个节点是否已经被更新过,如果被更新过,那么另一个节点的祖先一定是两个节点的LCA if(fa[R]!=R) printf("%d ",find(R)); } else if(u==R){ if(fa[L]!=L){ printf("%d ",find(L)); } } } void init(int n){ for(int i=0;i<=n;i++)fa[i]=i,in[i]=0,vis[i]=0,head[i]=0; tot=1; } int main(){ int t; scanf("%d",&t); while(t--){ tot=1; int n; scanf("%d",&n); init(n); for(int i=1;i<n;i++){ int l,r; scanf("%d %d",&l,&r); add(l,r); in[r]++;//依旧还是从入度为0的点开始 } scanf("%d%d",&L,&R); for(int i=1;i<=n;i++) if(!in[i]){ tarjan(i); break; } } return 0; }
3.RMQ(在线算法)
RMQ(Range Minimum/Maximum Query)区间最大最小查询,从表面上区间最大最小似乎和LCA一点关系都没有.但是如果引入欧拉序列,那么我们就可以从欧拉序列的性质解决LCA问题。
什么是欧拉序列?欧拉序列就是访问到节点的时候将它入队,回溯回来的时候再入队一次,每个节点仅入队2次。但是对于LCA转RMQ上要略微做些修改。我们将每一次访问到节点都入队,将从子树回来的节点也统统入队。对于每次LCA相当于找两个节点在序列中第一出现的位置之间的最小深度的节点。为什么会有这个性质呢?其实很好理解,两个节点第一次出现的位置之间一定有一部分节点是来自两个节点之间路径上的节点。于是我们只要求得任意两点之间深度最小的节点就可以得到LCA,而区间最小恰恰是RMQ解决的问题,因此可以用RMQ维护区间最小值,O(1)的查询LCA

依旧是POJ1330

#include<bits/stdc++.h> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0) const int N=1e5+10; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps=1e-7; using namespace std; int head[N],to[N],nx[N],tot=1; bool deg[N]; int dep[N],n,cnt=1,que[N<<1],in[N],out[N]; void add(int u,int v){ nx[tot]=head[u]; to[tot]=v; head[u]=tot++; } struct RMQ { int st[N<<1][32]; inline void init_ST(){ for(int i=1;i<cnt;++i)st[i][0]=i; int k=31-__builtin_clz(cnt-1); for(int j=1;j<=k;++j){ for(int i=1;i+(1<<j)-1<cnt;++i){ int l=st[i][j-1],r=st[i+(1<<(j-1))][j-1]; if(dep[l]<=dep[r]){ st[i][j]=l; } else st[i][j]=r; } } } inline int rmq(int l,int r){ int k=31-__builtin_clz(r-l+1); int L=st[l][k],R=st[r-(1<<k)+1][k]; if(dep[L]<=dep[R])return L; else return R; } inline int lca(int l,int r){ int L=in[l],R=in[r]; if(L>R)swap(L,R); return que[rmq(L,R)]; } }rmq; void dfs(int u,int d){ que[cnt]=u; in[u]=cnt; dep[cnt++]=d; for(int i=head[u];i;i=nx[i]){ int v=to[i]; dfs(v,d+1); que[cnt]=u; dep[cnt++]=d; } } int main(){ int T; scanf("%d",&T); while(T--){ cnt=1; tot=1;memset(head,0,sizeof(head));memset(deg,0,sizeof(deg)); scanf("%d",&n); for(int i=1;i<n;i++){ int u,v;scanf("%d%d",&u,&v); add(u,v); deg[v]=1; } for(int i=1;i<=n;i++){ if(!deg[i]){ dfs(i,1); break; } } rmq.init_ST(); int l,r;scanf("%d%d",&l,&r); printf("%d ",rmq.lca(l,r)); } return 0; } /* */
