[BZOJ4399]魔法少女LJJ

题目大意：给你一个图，有一些操作要你实现。具体操作见题目。

解题思路：首先，我认真地读着题目，当我看到

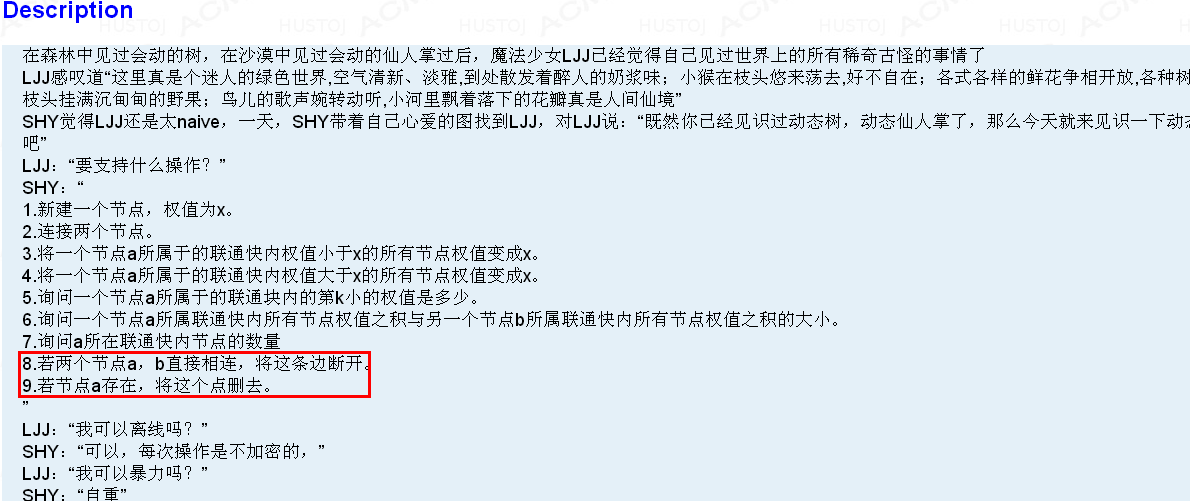
这两行时，感觉有点不知所措。然而，

！！！

这充分说明了出题者脑洞之大。orz

当我历经千辛万苦写完代码打算测样例时，发现样例第11行出现了个操作9！而且还影响答案！相当于这题连样例都没有。

吐槽完了，回归正题。这道题不难看出，需要用线段树合并来做。并且在建立权值线段树之前，先得把数据离散化（数据<=1000000000）。

对于操作3和4，删除所有需要改变的节点，然后加进权值x里即可。

对于操作6，可以用$log_{}ab=log_{}a+log_{}b$的方式进行比较。

其他操作随便搞搞就行了。

数组不要开太小，当然也不能开太大。

C++ Code：

#include<cstdio>
#include<algorithm>
#include<map>
#include<cmath>
#define N 6000000
using namespace std;
int m,n=0,mx=0,node=0,u,v,x,cnt;
int fa[400001],root[400001],ld[N],rd[N],mp[400001],d[N];
double lg[N]={0};
struct operation{
	int c,a,b;
}ol[400001];
map<int,int>p;
inline void update(int k){
	d[k]=d[ld[k]]+d[rd[k]];
	lg[k]=lg[ld[k]]+lg[rd[k]];
}
int dad(int x){return fa[x]==x?x:(fa[x]=dad(fa[x]));}
void add(int& k,int l,int r,int x,int num){
	if(!k)k=++node;
	if(l==r){
		d[k]+=num;
		lg[k]+=num*log(mp[x]);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)add(ld[k],l,mid,x,num);else
	add(rd[k],mid+1,r,x,num);
	update(k);
}
inline int merge(int u,int v,int l,int r){
	if(!u||!v)return u|v;
	if(l==r){
		d[u]+=d[v];
		lg[u]+=lg[v];
		return u;
	}
	int mid=l+r>>1;
	ld[u]=merge(ld[u],ld[v],l,mid);
	rd[u]=merge(rd[u],rd[v],mid+1,r);
	update(u);
	return u;
}
int query(int k,int l,int r,int L,int R){
	if(L<=l&&r<=R)return d[k];
	int m=l+r>>1,ans=0;
	if(L<=m)ans+=query(ld[k],l,m,L,R);
	if(m<R)ans+=query(rd[k],m+1,r,L,R);
	return ans;
}
void del(int k,int l,int r,int L,int R){
	if(!d[k])return;
	if(l==r){
		d[k]=0;
		lg[k]=0;
		return;
	}
	int m=l+r>>1;
	if(L<=m)del(ld[k],l,m,L,R);
	if(m<R)del(rd[k],m+1,r,L,R);
	update(k);
}
int ask(int k,int l,int r,int sum){
	if(l==r)return l;
	int mid=l+r>>1;
	if(sum<=d[ld[k]])return ask(ld[k],l,mid,sum);
	return ask(rd[k],mid+1,r,sum-d[ld[k]]);
}
int main(){
	scanf("%d",&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&ol[i].c);
		if(ol[i].c==1){
			scanf("%d",&ol[i].a);
			mp[++mx]=ol[i].a;
		}else
		if(ol[i].c==3||ol[i].c==4){
			scanf("%d%d",&ol[i].a,&ol[i].b);
			mp[++mx]=ol[i].b;
		}else
		if(ol[i].c==2||ol[i].c==5||ol[i].c==6)scanf("%d%d",&ol[i].a,&ol[i].b);else
		scanf("%d",&ol[i].a);
	}
	sort(mp+1,mp+mx+1);
	mx=unique(mp+1,mp+mx+1)-mp-1;
	for(int i=1;i<=mx;i++)p[mp[i]]=i;
	for(int i=1;i<=m;i++){
		if(ol[i].c==1){
			++n;
			fa[n]=n;
			add(root[n],1,mx,p[ol[i].a],1);
		}else
		if(ol[i].c==2){
			u=dad(ol[i].a),v=dad(ol[i].b);
			if(u!=v){
				fa[v]=u;
				root[u]=merge(root[u],root[v],1,mx);
			}
		}else
		if(ol[i].c==3){
			u=dad(ol[i].a),x=p[ol[i].b];
			if(x==1)continue;
			cnt=query(root[u],1,mx,1,x-1);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,1,x-1);
		}else
		if(ol[i].c==4){
			u=dad(ol[i].a),x=p[ol[i].b];
			if(x==mx)continue;
			cnt=query(root[u],1,mx,x+1,mx);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,x+1,mx);
		}else
		if(ol[i].c==5){
			u=dad(ol[i].a);
			printf("%d
",mp[ask(root[u],1,mx,ol[i].b)]);
		}else
		if(ol[i].c==6){
			u=dad(ol[i].a),v=dad(ol[i].b);
			printf("%d
",lg[root[u]]>lg[root[v]]?1:0);
		}else
		if(ol[i].c==7)
		printf("%d
",d[root[dad(ol[i].a)]]);
	}
	return 0;
}

 

然而我看到最快的人的耗时才1800+ms，我却有18000+ms，就感觉不爽，于是加了读入优化(比平常的读优更高级)。

C++ Code：

#include<cstdio>
#include<algorithm>
#include<map>
#include<cmath>
#include<cctype>
#define N 6000000
using namespace std;
int m,n=0,mx=0,node=0,u,v,x,cnt;
int fa[400001],root[400001],ld[N],rd[N],mp[400001],d[N];
double lg[N]={0};
char buf[30000020];
int bufpos;
inline void init(){
	buf[fread(buf,1,30000020,stdin)]='';
    bufpos=0;
}
inline int readint(){
	int p=0;
	for(;!isdigit(buf[bufpos]);bufpos++);
	for(;isdigit(buf[bufpos]);bufpos++)
	p=p*10+buf[bufpos]-'0';
	return p;
}
struct operation{
	int c,a,b;
}ol[400001];
map<int,int>p;
inline void update(int k){
	d[k]=d[ld[k]]+d[rd[k]];
	lg[k]=lg[ld[k]]+lg[rd[k]];
}
int dad(int x){return fa[x]==x?x:(fa[x]=dad(fa[x]));}
void add(int& k,int l,int r,int x,int num){
	if(!k)k=++node;
	if(l==r){
		d[k]+=num;
		lg[k]+=num*log(mp[x]);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)add(ld[k],l,mid,x,num);else
	add(rd[k],mid+1,r,x,num);
	update(k);
}
inline int merge(int u,int v,int l,int r){
	if(!u||!v)return u|v;
	if(l==r){
		d[u]+=d[v];
		lg[u]+=lg[v];
		return u;
	}
	int mid=l+r>>1;
	ld[u]=merge(ld[u],ld[v],l,mid);
	rd[u]=merge(rd[u],rd[v],mid+1,r);
	update(u);
	return u;
}
int query(int k,int l,int r,int L,int R){
	if(L<=l&&r<=R)return d[k];
	int m=l+r>>1,ans=0;
	if(L<=m)ans+=query(ld[k],l,m,L,R);
	if(m<R)ans+=query(rd[k],m+1,r,L,R);
	return ans;
}
void del(int k,int l,int r,int L,int R){
	if(!d[k])return;
	if(l==r){
		d[k]=0;
		lg[k]=0;
		return;
	}
	int m=l+r>>1;
	if(L<=m)del(ld[k],l,m,L,R);
	if(m<R)del(rd[k],m+1,r,L,R);
	update(k);
}
int ask(int k,int l,int r,int sum){
	if(l==r)return l;
	int mid=l+r>>1;
	if(sum<=d[ld[k]])return ask(ld[k],l,mid,sum);
	return ask(rd[k],mid+1,r,sum-d[ld[k]]);
}
int main(){
	init();
	m=readint();
	for(int i=1;i<=m;i++){
		ol[i].c=readint();
		if(ol[i].c==1)mp[++mx]=ol[i].a=readint();else
		if(ol[i].c==3||ol[i].c==4){
			ol[i].a=readint();
			mp[++mx]=ol[i].b=readint();
		}else
		if(ol[i].c==2||ol[i].c==5||ol[i].c==6)ol[i].a=readint(),ol[i].b=readint();else
		ol[i].a=readint();
	}
	sort(mp+1,mp+mx+1);
	mx=unique(mp+1,mp+mx+1)-mp-1;
	for(int i=1;i<=mx;i++)p[mp[i]]=i;
	for(int i=1;i<=m;i++){
		if(ol[i].c==1){
			++n;
			fa[n]=n;
			add(root[n],1,mx,p[ol[i].a],1);
		}else
		if(ol[i].c==2){
			u=dad(ol[i].a),v=dad(ol[i].b);
			if(u!=v){
				fa[v]=u;
				root[u]=merge(root[u],root[v],1,mx);
			}
		}else
		if(ol[i].c==3){
			u=dad(ol[i].a),x=p[ol[i].b];
			if(x==1)continue;
			cnt=query(root[u],1,mx,1,x-1);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,1,x-1);
		}else
		if(ol[i].c==4){
			u=dad(ol[i].a),x=p[ol[i].b];
			if(x==mx)continue;
			cnt=query(root[u],1,mx,x+1,mx);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,x+1,mx);
		}else
		if(ol[i].c==5){
			u=dad(ol[i].a);
			printf("%d
",mp[ask(root[u],1,mx,ol[i].b)]);
		}else
		if(ol[i].c==6){
			u=dad(ol[i].a),v=dad(ol[i].b);
			printf("%d
",lg[root[u]]>lg[root[v]]?1:0);
		}else
		if(ol[i].c==7)
		printf("%d
",d[root[dad(ol[i].a)]]);
	}
	return 0;
}

（上面是读优）快了3000ms左右，然而还是好慢。

不过能说明在数据较大的题目里，读入优化能大大提高代码效率。

那个1800+ms的是怎么做到的？orz

 

后来我又想到map可能会拖慢时间，于是map改成了直接用lower_bound()找。又快了2500ms左右。

C++ Code：

 

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cctype>
#define N 6000000
using namespace std;
int m,n=0,mx=0,node=0,u,v,x,cnt;
int fa[400001],root[400001],ld[N],rd[N],mp[400001],d[N];
double lg[N]={0};
char buf[30000020];
int bufpos;
inline int fnd(int x){
	return lower_bound(mp+1,mp+1+mx,x)-mp;
}
inline void init(){
	buf[fread(buf,1,30000020,stdin)]='';
    bufpos=0;
}
inline int readint(){
	int p=0;
	for(;!isdigit(buf[bufpos]);bufpos++);
	for(;isdigit(buf[bufpos]);bufpos++)
	p=p*10+buf[bufpos]-'0';
	return p;
}
struct operation{
	int c,a,b;
}ol[400001];
inline void update(int k){
	d[k]=d[ld[k]]+d[rd[k]];
	lg[k]=lg[ld[k]]+lg[rd[k]];
}
int dad(int x){return fa[x]==x?x:(fa[x]=dad(fa[x]));}
void add(int& k,int l,int r,int x,int num){
	if(!k)k=++node;
	if(l==r){
		d[k]+=num;
		lg[k]+=num*log(mp[x]);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)add(ld[k],l,mid,x,num);else
	add(rd[k],mid+1,r,x,num);
	update(k);
}
inline int merge(int u,int v,int l,int r){
	if(!u||!v)return u|v;
	if(l==r){
		d[u]+=d[v];
		lg[u]+=lg[v];
		return u;
	}
	int mid=l+r>>1;
	ld[u]=merge(ld[u],ld[v],l,mid);
	rd[u]=merge(rd[u],rd[v],mid+1,r);
	update(u);
	return u;
}
int query(int k,int l,int r,int L,int R){
	if(L<=l&&r<=R)return d[k];
	int m=l+r>>1,ans=0;
	if(L<=m)ans+=query(ld[k],l,m,L,R);
	if(m<R)ans+=query(rd[k],m+1,r,L,R);
	return ans;
}
void del(int k,int l,int r,int L,int R){
	if(!d[k])return;
	if(l==r){
		d[k]=0;
		lg[k]=0;
		return;
	}
	int m=l+r>>1;
	if(L<=m)del(ld[k],l,m,L,R);
	if(m<R)del(rd[k],m+1,r,L,R);
	update(k);
}
int ask(int k,int l,int r,int sum){
	if(l==r)return l;
	int mid=l+r>>1;
	if(sum<=d[ld[k]])return ask(ld[k],l,mid,sum);
	return ask(rd[k],mid+1,r,sum-d[ld[k]]);
}
int main(){
	init();
	m=readint();
	for(int i=1;i<=m;i++){
		ol[i].c=readint();
		if(ol[i].c==1)mp[++mx]=ol[i].a=readint();else
		if(ol[i].c==3||ol[i].c==4){
			ol[i].a=readint();
			mp[++mx]=ol[i].b=readint();
		}else
		if(ol[i].c==2||ol[i].c==5||ol[i].c==6)ol[i].a=readint(),ol[i].b=readint();else
		ol[i].a=readint();
	}
	sort(mp+1,mp+mx+1);
	mx=unique(mp+1,mp+mx+1)-mp-1;
	for(int i=1;i<=m;i++){
		if(ol[i].c==1){
			++n;
			fa[n]=n;
			add(root[n],1,mx,fnd(ol[i].a),1);
		}else
		if(ol[i].c==2){
			u=dad(ol[i].a),v=dad(ol[i].b);
			if(u!=v){
				fa[v]=u;
				root[u]=merge(root[u],root[v],1,mx);
			}
		}else
		if(ol[i].c==3){
			u=dad(ol[i].a),x=fnd(ol[i].b);
			if(x==1)continue;
			cnt=query(root[u],1,mx,1,x-1);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,1,x-1);
		}else
		if(ol[i].c==4){
			u=dad(ol[i].a),x=fnd(ol[i].b);
			if(x==mx)continue;
			cnt=query(root[u],1,mx,x+1,mx);
			add(root[u],1,mx,x,cnt);
			del(root[u],1,mx,x+1,mx);
		}else
		if(ol[i].c==5){
			u=dad(ol[i].a);
			printf("%d
",mp[ask(root[u],1,mx,ol[i].b)]);
		}else
		if(ol[i].c==6){
			u=dad(ol[i].a),v=dad(ol[i].b);
			printf("%d
",lg[root[u]]>lg[root[v]]?1:0);
		}else
		if(ol[i].c==7)
		printf("%d
",d[root[dad(ol[i].a)]]);
	}
	return 0;
}