狼抓兔子（平面图转对偶图）

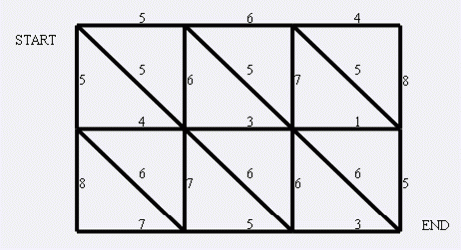
狼抓兔子（平面图转对偶图）

面对下面这样一个网格的地形：

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

没什么好说的，放张图就知道了：

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;

const int maxn=3e6, INF=1e9;
int n, m, src, dst;
struct Edge{
    int to, nxt, v;
}e[maxn*2];
int fir[maxn], cnte;
void addedge(int x, int y, int v){
    Edge &ed=e[++cnte];
    ed.to=y; ed.nxt=fir[x]; ed.v=v; fir[x]=cnte;
    Edge &ed2=e[++cnte];
    ed2.to=x; ed2.nxt=fir[y]; ed2.v=v; fir[y]=cnte;
}

int dis[maxn], num[maxn];
struct cmp{
    bool operator ()(int x, int y){ return dis[x]>dis[y]; }
};
priority_queue<int, vector<int>, cmp> q;
int dijkstra(){
    for (int i=1; i<=dst; ++i) dis[i]=INF;
    int u, v; q.push(src); num[src]=1;
    for (int i=0; i<=dst; ++i){
        while (num[q.top()]>1) --num[q.top()], q.pop();
        u=q.top(); q.pop(); --num[u];
        for (int j=fir[u]; ~j; j=e[j].nxt){
            v=e[j].to;
            if (dis[u]+e[j].v<dis[v]){
                dis[v]=dis[u]+e[j].v;
                ++num[v]; q.push(v);
            }
        }
    }
    return dis[dst];
}

int main(){
    memset(fir, -1, sizeof(fir));
    scanf("%d%d", &n, &m); int t; src=0; dst=n*m+1;
    for (int i=1; i<m; ++i){ scanf("%d", &t); addedge(src, i*2, t); }
    for (int i=1, cur=1; i<n-1; ++i)
        for (int j=1; j<m; ++j, cur+=2){
            scanf("%d", &t);
            addedge(cur, cur+2*m-1, t);
        }
    for (int i=1; i<m; ++i){ scanf("%d", &t); addedge(dst-2*(m-i), dst, t); }
    for (int i=1, cur=2; i<n; ++i){
        scanf("%d", &t); addedge(cur-1, dst, t);
        for (int j=1; j<m-1; ++j, cur+=2){
            scanf("%d", &t);
            addedge(cur, cur+1, t);
        }
        scanf("%d", &t); addedge(0, cur, t); cur+=2;
    }
    for (int i=1, cur=1; i<n; ++i)
        for (int j=1; j<m; ++j, cur+=2){
            scanf("%d", &t); addedge(cur, cur+1, t); }
    printf("%d
", dijkstra());
    return 0;
}