题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋, 也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是:
L×Kmathrm{L} imes mathrm{K}L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入输出格式
输入格式:第一行两个用空格分离的正整数 n 和 m,代表宝藏屋的个数和道路数。
接下来 m 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1~n),和这条道路的长度 v。
输出格式:输出共一行,一个正整数,表示最小的总代价。
输入输出样例
说明
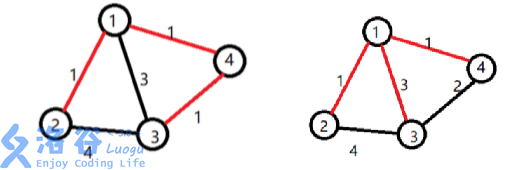
【样例解释1】
小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→21 o 21→2,挖掘了 2 号宝 藏。开发了道路 1→41 o 41→4,挖掘了 4 号宝藏。还开发了道路 4→34 o 34→3,挖掘了 3 号宝 藏。工程总代价为:1×1+1×1+1×2=41 imes 1 + 1 imes 1 + 1 imes 2 = 4 1×1+1×1+1×2=4
【样例解释2】
小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→21 o 21→2,挖掘了 2 号宝 藏。开发了道路 1→31 o 31→3,挖掘了 3 号宝藏。还开发了道路 1→41 o 41→4,挖掘了 4 号宝 藏。工程总代价为:1×1+3×1+1×1=51 imes 1 + 3 imes 1 + 1 imes 1 = 51×1+3×1+1×1=5
【数据规模与约定】
对于 20%的数据: 保证输入是一棵树,1≤n≤81 le n le 81≤n≤8,v≤5000v le 5000v≤5000 且所有的 v 都相等。
对于 40%的数据: 1≤n≤81 le n le 81≤n≤8,0≤m≤10000 le m le 10000≤m≤1000,v≤5000v le 5000v≤5000 且所有的 v 都相等。
对于 70%的数据: 1≤n≤81 le n le 81≤n≤8,0≤m≤10000 le m le 10000≤m≤1000,v≤5000v le 5000v≤5000
对于 100%的数据: 1≤n≤121 le n le 121≤n≤12,0≤m≤10000 le m le 10000≤m≤1000,v≤500000v le 500000v≤500000
题解
状压dp其实很明显,n<=12 考场一眼状压
我们设f[s]表示已经打通了集合s中的点的最小代价,则对于集合中所有的点的边,若能到达一个不在集合中的点v,新状态为e = s | (1 << v - 1),则f[e] = min(f[e],f[s] + w * g[s].d[u]);
其中g[s]储存的是s状态下各点的深度,由u点转移,那么代价就是【边权】w * g[s].d[u]
但是要注意,一个最优代价可能有多种深度方案,所以g[s]实际上应该是一个表,储存多个可能的深度【考场上就没注意想】
总的复杂度是O(2 ^ n * n * m)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define fo(i,x,y) for (int i = (x); i <= (y); i++)
#define Redge(u) for (int k = head[u]; k != -1; k = edge[k].next)
using namespace std;
const int maxn = 15,maxm = 2005,maxv = 1 << 13,INF = 1000000000;
inline int read(){
int out = 0,flag = 1;char c = getchar();
while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = out * 10 + c - 48; c = getchar();}
return out * flag;
}
int head[maxn],nedge = 0;
struct EDGE{
int to,w,next;
}edge[maxm];
inline void build(int u,int v,int w){
edge[nedge] = (EDGE) {v,w,head[u]};
head[u] = nedge++;
edge[nedge] = (EDGE) {u,w,head[v]};
head[v] = nedge++;
}
int f[maxv],n,m,mv;
struct node{
int d[maxn];
node() {memset(d,0,sizeof(d));}
node(int u) {memset(d,0,sizeof(d)); d[u] = 1;}
};
vector<node> g[maxv];
void solve(){
for (int i = 1; i <= mv; i++) f[i] = INF;
for (int i = 1; i <= n; i++){
g[1 << (i - 1)].push_back(node(i));
f[1 << (i - 1)] = 0;
}
int to,e,t;
for (int s = 1; s <= mv; s++){
for (int i = 1; i <= n; i++){
if ((s | (1 << (i - 1))) == s){
Redge(i){
to = edge[k].to;
e = 1 << (to - 1);
t = s | e;
if (t != s){
for (unsigned int l = 0; l < g[s].size(); l++){
if (f[t] > f[s] + edge[k].w * g[s][l].d[i]){
f[t] = f[s] + edge[k].w * g[s][l].d[i];
g[t].clear();
g[t].push_back(g[s][l]);
g[t][0].d[to] = g[s][l].d[i] + 1;
}else if (f[t] == f[s] + edge[k].w * g[s][l].d[i]){
g[t].push_back(g[s][l]);
g[t][g[t].size() - 1].d[to] = g[s][l].d[i] + 1;
}
}
}
}
}
}
}
printf("%d
",f[mv]);
}
void init(){
fill(head,head + maxn,-1);
n = read(); m = read(); mv = (1 << n) - 1;
int a,b,w;
while (m--){
a = read(); b = read(); w = read();
build(a,b,w);
}
}
int main()
{
init();
solve();
return 0;
}