6/12
2016 Multi-University Training Contest 4
官方题解
KMP+DP A Another Meaning(CYD)
题意:
给一段字符,同时给定你一个单词,这个单词有双重意思,字符串中可能会有很多这种单词,求这句话的意思总数:hehe。
思路:
可以用kmp算法快速求出串中的单词数量,若单词是分开的,每个单词有两种意思,可以直接相乘,若两个及以上单词在原串中是有交集的,那么数量不是直接相乘,发现这片连在一起的单词数量dp[i]=dp[i-1]+dp[j];若i是连在一起的第一个数,dp[i]是2,j是与i不直接相连的最大那个单词位置,若这串的第一个单词也与之相连,那么dp[j]=1;这样就可以算出总数了。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005;
const long long mod=1000000007;
int f[maxn],n,m,s;
int a[maxn];
long long b[maxn];
char P[maxn],T[maxn];
void getFail()
{
f[0]=0;f[1]=0;
for(int i=1;i<m;i++)
{
int j=f[i];
while(j && P[i]!=P[j])
j=f[j];
f[i+1]= P[i] == P[j] ? j+1 : 0;
}
}
int main()
{
int t,cas=1;
int i,j;
scanf("%d",&t);
while(t--)
{
memset(f,0,sizeof(f));
s=0;
b[0]=1;a[0]=-1;
scanf("%s",T);
scanf("%s",P);
n=strlen(T),m=strlen(P);
getFail();
long long ans=1;
int cnt=0,line=-1;
j=0;
for(i=0;i<n;i++)
{
while(j && P[j]!=T[i]) j=f[j];
if(P[j]==T[i]) j++;
if(j==m)
{
if(i-m+1>line)
{
ans=(ans*b[s])%mod;
a[++s]=i;
b[s]=2;
cnt=1,line=i;
}
else
{
int k=lower_bound(a+1,a+1+s,i-m+1)-a;
long long c=b[k-1];
if(s-k+1>=cnt)
c=1;
a[++s]=i;
b[s]=(c+b[s-1])%mod;
cnt++,line=i;
}
j=0,i=i-m+1;
}
}
ans=(ans*b[s])%mod;
printf("Case #%d: %I64d
",cas++,ans);
}
return 0;
}
中国剩余定理+容斥原理 E Lucky7(BH)
题意:
问[L,R]区间内所有满足条件的数的个数,条件:and
思路:
看到n的范围应该能想到可以用状态压缩来枚举(pi,ai)的组合,求这个有什么用呢?可以从反面考虑,先求出“在[L,R]范围内,是7的倍数且”的个数,然后用”是7的倍数“的个数减之就是答案。前者可以用中国剩余定理以及状态压缩枚举方程组来得到,注意要是在7的倍数的条件下,所以每次取出的方程组一定要有(p=7, a=0)的方程组。另外,小于n的个数内是k的倍数的个数为n/k。
代码:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 20;
ll a[N], m[N];
ll ta[N], tm[N];
ll L, R;
int n, k;
void ex_GCD(ll a, ll b, ll &x, ll &y, ll &d) {
if (!b) {
x = 1; y = 0; d = a;
} else {
ex_GCD (b, a % b, y, x, d);
y -= a / b * x;
}
}
ll mul_mod(ll a, ll b, ll mod) {
ll ret = 0;
a = (a % mod + mod) % mod;
b = (b % mod + mod) % mod;
while (b) {
if (b & 1) {
ret += a;
if (ret >= mod) ret -= mod;
}
b >>= 1;
a <<= 1;
if (a >= mod) a -= mod;
}
return ret;
}
ll M;
ll China(int k, ll *a, ll *m) {
ll x, y, ret = 0, d;
for (int i=0; i<=k; ++i) {
ll w = M / m[i];
ex_GCD (w, m[i], x, y, d);
ret = (ret + mul_mod (mul_mod (x, w, M), a[i], M));
}
return (ret + M) % M;
}
ll solve(ll x) {
if (x == 0) return 0;
ll sub = 0;
int S = 1 << n;
ta[0] = 0; tm[0] = 7;
for (int i=1; i<S; ++i) {
int k = 0;
M = 7;
for (int j=0; j<n; ++j) {
if (i & (1 << j)) {
ta[++k] = a[j];
tm[k] = m[j];
M *= m[j];
}
}
ll res = China (k, ta, tm);
if (x < res) continue;
if (k & 1) sub -= (x - res) / M + 1;
else sub += (x - res) / M + 1;
}
//ret < 0
return x / 7 + sub;
}
int main() {
int T;
scanf ("%d", &T);
for (int cas=1; cas<=T; ++cas) {
scanf ("%d%I64d%I64d", &n, &L, &R);
for (int i=0; i<n; ++i) {
scanf ("%I64d%I64d", m+i, a+i);
}
printf ("Case #%d: %I64d
", cas, solve (R) - solve (L-1));
}
return 0;
}
后缀数组 F Substring(BH)
题意:
问一个字符串里至少包含一个字符X的不同的子串的个数。
思路:
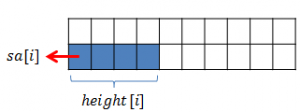
后缀数组可以较方便的处理LCP(最长公共前缀)。方法如下图所示:设有一个字符串为"aabaaaab",可以对所有后缀按照字典序从小到大排序,排好序后相邻的后缀的相同前缀长度就是它们的LCP,那么这题要求不相同的子串,所以这些相同的前缀肯定不能多次统计,比如aab和aabaaaab,b是要求字符,那么aab只能统计一次,对于aabaaaab它能贡献的子串只能是aabaaaab。如果要求字符X,只需要记录距离后缀i最近的字符X的位置。

代码:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
struct Suffix_Array {
int n, len, s[N];
int sa[N], rank[N], height[N];
int tmp_one[N], tmp_two[N], c[N];
void init_str(char *str);
void build_sa(int m = 128);
void get_height();
void print();
}SA;
void Suffix_Array::print() {
puts ("sa[] and height[]:");
for (int i=0; i<n; ++i) {
printf ("%2d ", sa[i]);
}
puts ("");
for (int i=0; i<n; ++i) {
printf ("%2d ", height[i]);
}
puts ("");
}
char str[N];
int nex[N];
char q[2];
ll solve() {
SA.init_str (str);
SA.build_sa ();
SA.get_height ();
ll ret = 0;
int len = SA.len;
nex[len] = len;
for (int i=len-1; i>=0; --i) {
nex[i] = str[i] == q[0] ? i : nex[i+1];
}
for (int i=1; i<=len; ++i) {
ret += (len - 1) - std::max (SA.sa[i] + SA.height[i], nex[SA.sa[i]]) + 1;
}
return ret;
}
int main() {
int T;
scanf ("%d", &T);
for (int cas=1; cas<=T; ++cas) {
scanf ("%s", &q);
scanf ("%s", &str);
printf ("Case #%d: %I64d
", cas, solve ());
}
return 0;
}
void Suffix_Array::init_str(char *str) {
n = 0;
len = strlen (str);
for (int i=0; i<len; ++i) {
s[n++] = str[i] - 'a' + 1;
}
s[n++] = 0; //n = strlen (str) + 1
}
void Suffix_Array::get_height() {
for (int i=0; i<n; ++i) rank[sa[i]] = i;
int k = height[0] = 0;
for (int i=0; i<n-1; ++i) {
if (k) k--;
int j = sa[rank[i]-1];
while (s[i+k] == s[j+k]) k++;
height[rank[i]] = k;
}
}
//m = max (r[i]) + 1,一般字符128足够了
void Suffix_Array::build_sa(int m) {
int i, j, p, *x = tmp_one, *y = tmp_two;
for (i=0; i<m; ++i) c[i] = 0;
for (i=0; i<n; ++i) c[x[i]=s[i]]++;
for (i=1; i<m; ++i) c[i] += c[i-1];
for (i=n-1; i>=0; --i) sa[--c[x[i]]] = i;
for (j=1, p=1; p<n; j<<=1, m=p) {
for (p=0, i=n-j; i<n; ++i) y[p++] = i;
for (i=0; i<n; ++i) if (sa[i] >= j) y[p++] = sa[i] - j;
for (i=0; i<m; ++i) c[i] = 0;
for (i=0; i<n; ++i) c[x[y[i]]]++;
for (i=1; i<m; ++i) c[i] += c[i-1];
for (i=n-1; i>=0; --i) sa[--c[x[y[i]]]] = y[i];
std::swap (x, y);
for (p=1, x[sa[0]]=0, i=1; i<n; ++i) {
x[sa[i]] = (y[sa[i-1]] == y[sa[i]] && y[sa[i-1]+j] == y[sa[i]+j] ? p - 1 : p++);
}
}
}
贪心+LIS J The All-purpose Zero
题意:
有一串数,其中0可以变为任意整数,最长上升子序列是多长。
思路:
0可以转换成任意任何整数,就是说也可以转换为负数,那么最长上升子序列包含的数值一定含有全部0,那么就看其余正整数能否在数列中,也就是说是否会和0变化成的数字冲突,那么我们可以将每个权值S[i]减去i前面0的个数这个方法组成新的数列做LIS(O(nlogn)),最后加上0的数量。
代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
int s[100005],m,dp[100005];
int main()
{
int T,cas=1;
int i,j,k;
int n,num,x,ma;
scanf("%d",&T);
while(T--)
{
for(i=0;i<=100002;i++)
{
dp[i]=inf;
}
m=0,num=0,ma=0;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d",&x);
if(x==0)
{
num++;
}
else
{
s[++m]=x-num;
}
}
for(i=1;i<=m;i++)
{
int l=lower_bound(dp+1,dp+n+1,s[i])-dp;
dp[l]=s[i];
ma=max(l,ma);
}
printf("Case #%d: %d
",cas++,ma+num);
}
return 0;
}