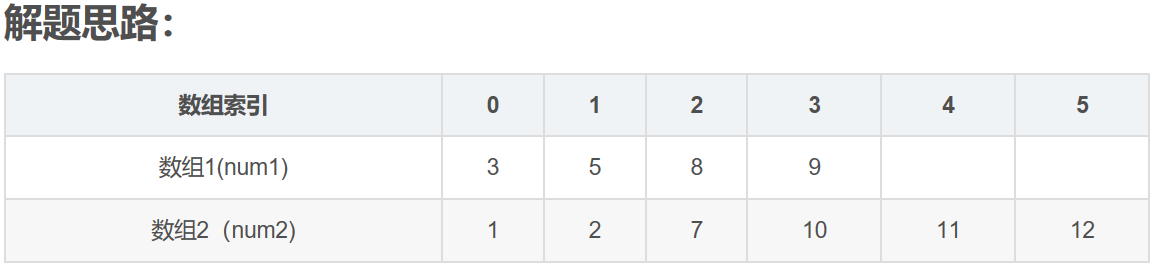
其中,N1=4,N2=6,size=4+6=10.
1,现在有的是两个已经排好序的数组,结果是要找出这两个数组中间的数值,如果两个数组的元素个数为偶数,则输出的是中间两个元素的平均值。
2,可以想象,如果将数组1随便切一刀(如在3和5之间切一刀),数组1将分成两份,数组1左别的元素的个数为1,右边的元素的个数为3。
由于数组1和数组2最终分成的左右两份的个数是确定的,都是所有元素的个数的一半(size/2=5)所以我们也可以知道,此时对数组2应该切的一刀的位置应该在10和11之间,数组2左边的个数为4,右边的个数为2.才能使两个数组左右两边的元素个数加起来的和(1+4=2+3)相等。
另外,我们记在数组1靠近这一刀的左别的元素为L1(3),右边元素为R1(5).同理,记在数组2靠近这一刀的左别的元素为L2(10),右边元素为R2(11).
如果这一刀的位置是正确的,则应该有的结果是
L1<=R2
L2<=R1
这样就能确保,左边的元素都小于右边的元素了。
3,所以,我们只需要直接找出在数组1切这一刀的正确位置就可以了。
为了减少查找次数,我们对短的数组进行二分查找。将在数组1切割的位置记为cut1,在数组2切割的位置记为cut2,cut2=(size/2)-cut1。
cut1,cut2分别表示的是数组1,数组2左边的元素的个数。
4,切这一刀的结果有三种
1)L1>R2 则cut1应该向左移,才能使数组1较多的数被分配到右边。
2)L2>R1 则cut1应该向右移,才能使数组1较多的数被分配到左边。
3)其他情况(L1<=R2 L2<=R1),cut1的位置是正确的,可以停止查找,输出结果。
5,其他说明
1)考虑到边界条件,就是cut的位置可能在边缘,就是cut1=0或者cut1=N1,cut2=0或者cut2=N2的这些情况,我们将min和max两个特殊值分别加在数组1和数组2的两端,就可以统一考虑了。还有N1个数为0的时候,直接输出结果即可。
2)为了减少查找时间,使用的是二分查找,就是cut1的位置是一半一半的查找的,实现时间只要log(N),不然就会超时。所以,我们不能只是简单地将cut1–或者cut1++,而是要记下每次cut1的区域范围,我们将cut1的范围记录下来,用[cutL,cutR]表示。一开始cut1的范围是[cutL,cutR]=[0,N1],
如果L1>R2 则cut1应该向左移,才能使数组1较多的数被分配到右边。cut1的范围就变成了[cutL,cut1-1],下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
如果L2>R1 则cut1应该向右移,才能使数组1较多的数被分配到左边。cut1的范围就变成了[cut1+1,cutR],下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
3)数组的元素个数和是奇数的情况下,中间的元素应该就是min(R1,R2),只需另外处理输出就可以了。
time log(min(m,n))
space o(1)
1 class Solution { 2 public static double findMedianSortedArrays(int[] nums1, int[] nums2) { 3 if(nums1.length > nums2.length){ 4 return findMedianSortedArrays(nums2, nums1); 5 } 6 int len = nums1.length + nums2.length; 7 int cut1 = 0; 8 int cut2 = 0; 9 int cutL = 0; 10 int cutR = nums1.length; 11 while(cut1 <= nums1.length){ 12 cut1 = (cutR - cutL)/2 + cutL; 13 cut2 = len/2 - cut1; 14 double L1 = (cut1 == 0 )? Integer.MIN_VALUE:nums1[cut1 - 1]; 15 double L2 = (cut2 == 0 )? Integer.MIN_VALUE:nums2[cut2 - 1]; 16 double R1 = (cut1 == nums1.length )? Integer.MAX_VALUE:nums1[cut1]; 17 double R2 = (cut2 == nums2.length )? Integer.MAX_VALUE:nums2[cut2]; 18 if(L1>R2){ 19 cutR = cut1 - 1; 20 }else if(L2 > R1){ 21 cutL = cut1 + 1; 22 }else{ 23 if(len %2 == 0){ 24 L1 = (L1 > L2) ? L1 : L2; 25 R1 = (R1 > R2 )? R2 : R1; 26 return (L1+R1)/2; 27 }else{ 28 R1 = (R1 < R2) ? R1 : R2; 29 return R1; 30 } 31 } 32 } 33 return -1; 34 } 35 36 }
转自https://blog.csdn.net/chen_xinjia/article/details/69258706
2019-03-11 23:06:05