【UVA1635】哑元

题意

给定n个数a₁，a₂，...a_n,依次求出相邻两数之和，将得到一个新数列。重复上述操作，最后结果将变成一个数。问这个数除以m的余数与哪些数无关？例如n=3，m=2时，第一次求和得到a₁+a₂，a₂+a₃，再求和得到a₁+2a₂+a₃，它除以2的余数和a₂无关。(1 ≤ n ≤ 100 000, 2 ≤ m ≤ 10⁹ )

分析

举的这个例子已经疯狂暗示了，怎么看都是二项式定理啊！！！

二项式定理就不写了，反正就是求组合数了，有一个递推的式子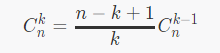

证明太显然了，直接拆成递推形式一眼就看出来了。于是可以利用它计算出C(n-1,i-1)的每一项，得到a_i的系数，再判断一下是不是m的倍数

直接递推太大了，会涉及到高精，于是利用唯一分解定理分解m，再比较各个质因子的指数与C(n-1,i-1)中的指数即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define N 100010
int n,m,cnt;
int p[N],c[N],ok[N];
vector<int>ans;
void divide(int k)
{
    cnt=0;
    memset(p,0,sizeof(p));
    memset(c,0,sizeof(c));
    int mx=(int)sqrt(k+1);
    for(int i=2;i<=mx;i++)
    {
        if(k%i==0)
        {
            p[++cnt]=i;
            while(k%i==0)c[cnt]++,k/=i;
        }
        if(k==1)break;
    }
    if(k>1)p[++cnt]=k,c[cnt]=1;
}

vector<int> solve()
{
    memset(ok,-1,sizeof(ok));
    vector<int>v;n--;
    for(int i=1;i<=cnt;i++)
    {
        int cm=0;
        for(int k=1;k<n;k++)
        {
            int a=n-k+1,b=k;
            while(a%p[i]==0)a/=p[i],cm++;
            while(b%p[i]==0)b/=p[i],cm--;
            if(cm<c[i])ok[k]=0;
        }
    }
    for(int i=1;i<n;i++)if(ok[i])v.push_back(i+1);
    return v;
}

int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        divide(m);
        ans=solve();
        printf("%d
", (int)ans.size());
        for (int i = 0; i < ans.size(); i++)
            printf("%d%c",ans[i],i==ans.size()-1?'
':' ');
        if (ans.size()==0) printf("
");
    }
    return 0;
}