[POJ 2653]Pick-up sticks

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.

Output

For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.

The picture to the right below illustrates the first case from input.

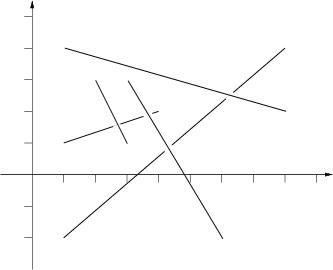
Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

Sample Output

Top sticks: 2, 4, 5.

Top sticks: 1, 2, 3.

题目大意

n个棍子，一个一个扔，如果扔在了别的棍子上，也就是说和别的棍子相交了，那么和它相交的棍子就会消失，求最后剩下的棍子的编号。

题解

考察的是线段与线段的相交判断。

判断两线段是否相交：

　　我们分两步确定两条线段是否相交：

　　(1)快速排斥试验

　　　　设以线段 $P_1P_2$ 为对角线的矩形为$R$， 设以线段 $Q_1Q_2$ 为对角线的矩形为$T$，如果$R$和$T$不相交，显然两线段不会相交。

　　(2)跨立试验
　　　　如果两线段相交，则两线段必然相互跨立对方。若$P_1P_2$跨立$Q_1Q_2$ ，则矢量 $( P_1 - Q_1 )$ 和$( P_2 - Q_1 )$位于矢量$( Q_2 - Q_1 )$ 的两侧，即$( P_1 - Q_1 ) × ( Q_2 - Q_1 ) * ( P_2 - Q_1 ) × ( Q_2 - Q_1 ) < 0$。上式可改写成$( P_1 - Q_1 ) × ( Q_2 - Q_1 ) * ( Q_2 - Q_1 ) × ( P_2 - Q_1 ) > 0$。当 $( P_1 - Q_1 ) × ( Q_2 - Q_1 ) = 0$ 时，说明 $( P_1 - Q_1 )$ 和 $( Q_2 - Q_1 )$共线，但是因为已经通过快速排斥试验，所以 $P_1$ 一定在线段 $Q_1Q_2$上；同理，$( Q_2 - Q_1 ) ×(P_2 - Q_1 ) = 0$ 说明 $P_2$ 一定在线段 $Q_1Q_2$上。所以判断$P_1P_2$跨立$Q_1Q_2$的依据是：$( P_1 - Q_1 ) × ( Q_2 - Q_1 ) * ( Q_2 - Q_1 ) × ( P_2 - Q_1 ) >= 0$。同理判断$Q_1Q_2$跨立$P_1P_2$的依据是：$( Q_1 - P_1 ) × ( P_2 - P_1 ) * ( P_2 - P_1 ) × ( Q_2 - P_1 ) >= 0$。具体情况如下图所示：

   

按理来说O(n²)绝对过不了，数据很水啊...

#include<set>
#include<map>
#include<ctime>
#include<cmath>
#include<queue>
#include<stack>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define LL long long
#define RE register
#define IL inline
using namespace std;
const int N=100000;

IL double Min(const double &a,const double &b){return a<b ? a:b;}
IL double Max(const double &a,const double &b){return a>b ? a:b;}

struct Point
{
    double x,y;
    Point (){}
    Point (double _x,double _y){x=_x;y=_y;}
    Point operator - (const Point &b)
    const{
        return Point(x-b.x,y-b.y);
    }
    double operator * (const Point &b)
    const{
        return x*b.y-y*b.x;
    }
};
struct Segment
{
    Point a,b;
    Segment (){}
    Segment (Point _a,Point _b){a=_a;b=_b;}
    bool operator & (const Segment &B)
    const{
        if (Min(a.x,b.x)>Max(B.a.x,B.b.x)||Min(B.a.x,B.b.x)>Max(a.x,b.x)) return 0;
        if (Min(a.y,b.y)>Max(B.a.y,B.b.y)||Min(B.a.y,B.b.y)>Max(a.y,b.y)) return 0;
        if (((B.a-b)*(a-b))*((B.b-b)*(a-b))<=0&&((a-B.b)*(B.a-B.b))*((b-B.b)*(B.a-B.b))<=0) return 1;
        return 0;
    }
}segment[N+5];

int n;

int main()
{
    while (~scanf("%d",&n)&&n)
    {
        for (RE int i=1;i<=n;i++) scanf("%lf%lf%lf%lf",&segment[i].a.x,&segment[i].a.y,&segment[i].b.x,&segment[i].b.y);
        printf("Top sticks:");
        for (RE  int i=1;i<n;i++)
        {
            RE int j;
            for (j=i+1;j<=n;j++) if (segment[i]&segment[j]) break;
            if (j>n) printf(" %d,",i);
        }
        printf(" %d.
",n);
    }
    return 0;
}