1 最小二乘法概述
自从开始做毕设以来,发现自己无时无刻不在接触最小二乘法。从求解线性透视图中的消失点,m元n次函数的拟合,包括后来学到的神经网络,其思想归根结底全都是最小二乘法。
1-1 “多线→一点”视角与“多点→一线”视角
最小二乘法非常简单,我把它分成两种视角描述:
(1)已知多条近似交汇于同一个点的直线,想求解出一个近似交点:寻找到一个距离所有直线距离平方和最小的点,该点即最小二乘解;
(2)已知多个近似分布于同一直线上的点,想拟合出一个直线方程:设该直线方程为y=kx+b,调整参数k和b,使得所有点到该直线的距离平方之和最小,设此时满足要求的k=k0,b=b0,则直线方程为y=k0x+b0。
1-2 思维拓展
这只是举了两个简单的例子,其实在现实生活中我们可以利用最小二乘法解决更为复杂的问题。比方说有一个未知系数的二元二次函数f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5,这里w0~w5为未知的参数,为了确定下来这些参数,将会给定一些样本点(xi,yi,f(xi,yi)),然后通过调整这些参数,找到这样一组w0~w5,使得这些所有的样本点距离函数f(x,y)的距离平方之和最小。至于具体用何种方法来调整这些参数呢?有一种非常普遍的方法叫“梯度下降法”,它可以保证每一步调整参数,都使得f(x,y)朝比当前值更小的方向走,只要步长α选取合适,我们就可以达成这种目的。
而这里不得不提的就是神经网络了。神经网络其实就是不断调整权值w和偏置b,来使得cost函数最小,从这个意义上来讲它还是属于最小二乘法。更为可爱的一点是,神经网络的调参用到的仍是梯度下降法,其中最常用的当属随机梯度下降法。而后面伟大的bp算法,其实就是为了给梯度下降法做个铺垫而已,bp算法的结果是cost函数对全部权值和全部偏置的偏导,而得知了这些偏导,对于各个权值w和偏置b该走向何方就指明了方向。
因此,最小二乘法在某种程度上无异于机器学习中基础中的基础,且具有相当重要的地位。至于上面所说的“梯度下降法”以及“利用最小二乘法求解二元二次函数的w0~w5”,我将会在后面的博客中进行更加详细的探讨。
2 scipy库中的leastsq函数
当然,最小二乘法本身实现起来也是不难的,就如我们上面所说的不断调整参数,然后令误差函数Err不断减小就行了。我们将在下一次博客中详细说明如何利用梯度下降法来完成这个目标。
而在本篇博客中,我们介绍一个scipy库中的函数,叫leastsq,它可以省去中间那些具体的求解步骤,只需要输入一系列样本点,给出待求函数的基本形状(如我刚才所说,二元二次函数就是一种形状——f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5,在形状给定后,我们只需要求解相应的系数w0~w6),即可得到相应的参数。至于中间到底是怎么求的,这一部分内容就像一个黑箱一样。
2-1 函数形为y=kx+b
这一次我们给出函数形y=kx+b。这种情况下,待确定的参数只有两个:k和b。
此时给出7个样本点如下:
1 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 2 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
则使用leastsq函数求解其拟合直线的代码如下:
1 ###最小二乘法试验### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 7 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05]) 8 9 ###需要拟合的函数func及误差error### 10 def func(p,x): 11 k,b=p 12 return k*x+b 13 14 def error(p,x,y,s): 15 print s 16 return func(p,x)-y #x、y都是列表,故返回值也是个列表 17 18 #TEST 19 p0=[100,2] 20 #print( error(p0,Xi,Yi) ) 21 22 ###主函数从此开始### 23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的k、b 24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中 25 k,b=Para[0] 26 print"k=",k,' ',"b=",b 27 28 ###绘图,看拟合效果### 29 import matplotlib.pyplot as plt 30 31 plt.figure(figsize=(8,6)) 32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点 33 x=np.linspace(0,10,1000) 34 y=k*x+b 35 plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2) #画拟合直线 36 plt.legend() 37 plt.show()
我把里面需要注意的点提点如下:
1、p0里放的是k、b的初始值,这个值可以随意指定。往后随着迭代次数增加,k、b将会不断变化,使得error函数的值越来越小。
2、func函数里指出了待拟合函数的函数形状。
3、error函数为误差函数,我们的目标就是不断调整k和b使得error不断减小。这里的error函数和神经网络中常说的cost函数实际上是一回事,只不过这里更简单些而已。
4、必须注意一点,传入leastsq函数的参数可以有多个,但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。
5、leastsq的返回值是一个tuple,它里面有两个元素,第一个元素是k、b的求解结果,第二个元素我暂时也不知道是什么意思,先留下来。
其拟合效果图如下:
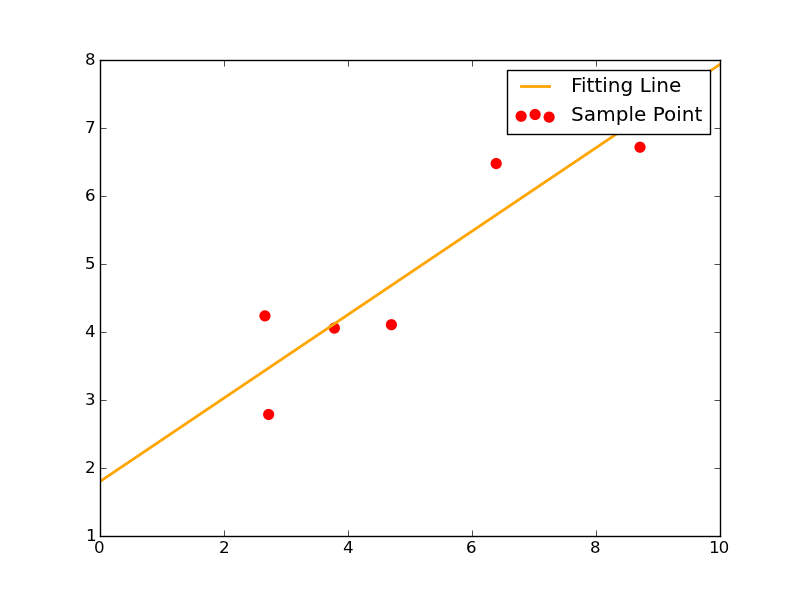
2-2 函数形为y=ax^2+bx+c
这一次我们给出函数形y=ax^2+bx+c。这种情况下,待确定的参数有3个:a,b和c。
此时给出7个样本点如下:
1 Xi=np.array([0,1,2,3,-1,-2,-3]) 2 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])
这一次的代码与2-1差不多,除了把待求参数再增加一个,换了一下训练样本,换了一下func中给出的函数形,几乎没有任何变化。
1 ###最小二乘法试验### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([0,1,2,3,-1,-2,-3]) 7 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7]) 8 9 ###需要拟合的函数func及误差error### 10 def func(p,x): 11 a,b,c=p 12 return a*x**2+b*x+c 13 14 def error(p,x,y,s): 15 print s 16 return func(p,x)-y #x、y都是列表,故返回值也是个列表 17 18 #TEST 19 p0=[5,2,10] 20 #print( error(p0,Xi,Yi) ) 21 22 ###主函数从此开始### 23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的a~c 24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中 25 a,b,c=Para[0] 26 print"a=",a,' ',"b=",b,"c=",c 27 28 ###绘图,看拟合效果### 29 import matplotlib.pyplot as plt 30 31 plt.figure(figsize=(8,6)) 32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点 33 x=np.linspace(-5,5,1000) 34 y=a*x**2+b*x+c 35 plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2) #画拟合曲线 36 plt.legend() 37 plt.show()
不过我们发现,它依旧能够非常顺利地解出待求的三个参数。其拟合情况如图所示:
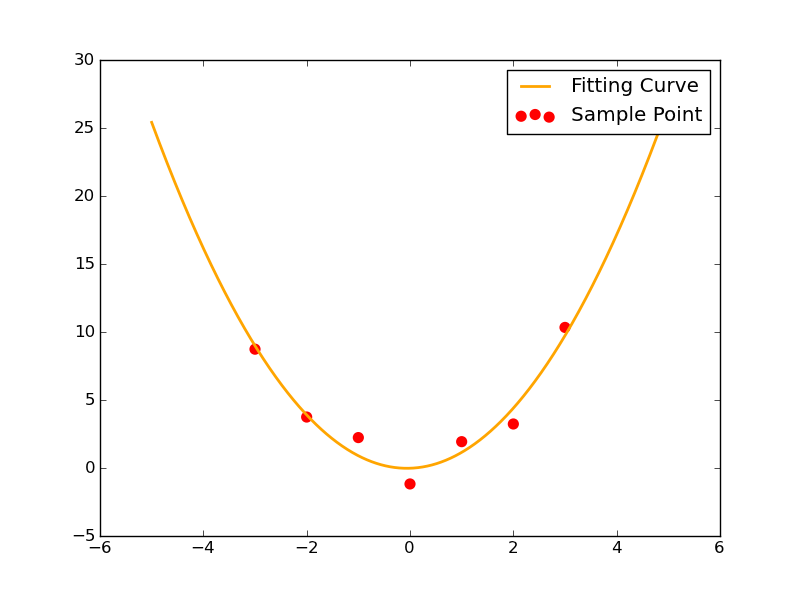
2-3 leastsq拟合y=kx+b可视化
本部分内容是建立在2-1代码的基础上,用Mayavi绘3D图,以简单地说明最小二乘法到底是怎么一回事。该部分知识用到了mgrid函数,具体是如何实施的请移步《Python闲谈(一)mgrid慢放》。
step 1:创建一个k矩阵和b矩阵。在mgrid扩展后,有:
(1)k=[k1,k2,k3,...,kn]
mgrid(k)(朝右扩展)=
[k1,k1,k1,...,k1]
[k2,k2,k2,...,k2]
[k3,k3,k3,...,k3]
...
[kn,kn,kn,...,kn]
(2)b=[b1,b2,b3,...,bn]
mgrid(b)(朝下扩展)=
[b1,b2,b3,...,bn]
[b1,b2,b3,...,bn]
[b1,b2,b3,...,bn]
...
[b1,b2,b3,...,bn]
其中k矩阵和b矩阵等大(皆为n维向量,或者说1*n的矩阵),且这两个矩阵里面的元素都非常密集。举个例子以说明什么叫矩阵中的元素很密集:a是个矩阵,假设aij 为a矩阵中第i行第j列元素,则aij 和 a{i+1}j 的差值很小,aij 和 ai{j+1} 的差值也很小。也就是同一行或者同一列中相邻的两个元素的值非常接近。为什么要让矩阵元素如此密集呢?因为我们的根本目的是用“密集的离散”来逼近“连续”,这里的思想就像微积分一样。
而放在这里,就是ku和k{u+1}很接近,bv和b{v+1}也很接近。
step 2:令k矩阵和b矩阵中的元素按照其位置一一对应。对应后的结果为:
Combine_kb=
[(k1,b1),(k1,b2),(k1,b3)...,(k1,bn)]
[(k2,b1),(k2,b2),(k2,b3)...,(k2,bn)]
[(k3,b1),(k3,b2),(k3,b3)...,(k3,bn)]
...
[(kn,b1),(kn,b2),(kn,b3)...,(kn,bn)]
step 3:对矩阵中每一个(ku,bv),我们分别求出该种情况下每一个训练样本点的误差平方之和,即有:
Err{(ku,bv)}=∑{i=1~m}((yi-(ku*xi+bv))**2)
其中m为给定的训练样本点的个数。例如在这里:
1 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 2 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
则有m=7。
什么意思呢?举个例子,当i=1的时候,这个时候把(x1,y1)(=(8.19,7.01))代入((yi-(ku*xi+bv))**2)式子里面,由于此时已经锁定(ku,bv),因此式中所有的数都是常数,我们可以解出一个常数((y1-(ku*x1+bv))**2)。然后依次令i=2,3,4,...,7,可以分别求解出一个((yi-(ku*xi+bv))**2)值来,这7个((yi-(ku*xi+bv))**2)值加起来即Err{(ku,bv)}。
注意了,最终我们算出的那个Err{(ku,bv)}将会存放到ku、bv对应的那个位置,比方说u=3,v=2:
mgrid(k)=
[k1,k1,k1,...,k1]
[k2,k2,k2,...,k2]
[k3,k3,k3,...,k3]
...
[kn,kn,kn,...,kn]
mgrid(b)=
[b1,b2,b3,...,bn]
[b1,b2,b3,...,bn]
[b1,b2,b3,...,bn]
...
[b1,b2,b3,...,bn]
则刚才算出来的Err{(k3,b2)}应该放在这个位置:
Err=
[Err11,Err12,Err13,...,Err1n]
[Err21,Err22,Err23,...,Err2n]
[Err31,Err32,Err33,...,Err3n]
...
[Errn1,Errn2,Errn3,...,Errnn]
如此这般对于每一对(ku,bv)都这样算,则上方的Err矩阵中每一个元素的值都可以算出来;将计算出的结果正确地放在Err矩阵中对应位置,即得到Err矩阵。
step 4:绘制曲面。
截至目前我们已经得到了两个重要矩阵Combine_kb和Err,其中Combine_kb提供点的x、y轴坐标,Err矩阵提供点的z轴坐标。
Combine_kb=
[(k1,b1),(k1,b2),(k1,b3)...,(k1,bn)]
[(k2,b1),(k2,b2),(k2,b3)...,(k2,bn)]
[(k3,b1),(k3,b2),(k3,b3)...,(k3,bn)]
...
[(kn,b1),(kn,b2),(kn,b3)...,(kn,bn)]
Err=
[Err11,Err12,Err13,...,Err1n]
[Err21,Err22,Err23,...,Err2n]
[Err31,Err32,Err33,...,Err3n]
...
[Errn1,Errn2,Errn3,...,Errnn]
我们再将这两个矩阵合并一下得到Combine_kbErr矩阵:
Combine_kbErr=
[(k1,b1,Err11),(k1,b2,Err12),(k1,b3,Err13)...,(k1,bn,Err1n)]
[(k2,b1,Err21),(k2,b2,Err22),(k2,b3,Err23)...,(k2,bn,Err2n)]
[(k3,b1,Err31),(k3,b2,Err32),(k3,b3,Err33)...,(k3,bn,Err3n)]
...
[(kn,b1,Errn1),(kn,b2,Errn2),(kn,b3,Errn3)...,(kn,bn,Errnn)]
在三维空间直角坐标系下绘制出Combine_kbErr中的每一个点,然后将这些点与其各自相邻的点连起来,则得到我们想要的Err(k,b)函数曲面。
step 5:本部分代码如下:
1 """part 2""" 2 ###定义一个函数,用于计算在k、b已知时∑((yi-(k*xi+b))**2)### 3 def S(k,b): 4 ErrorArray=np.zeros(k.shape) #k的shape事实上同时也是b的shape 5 for x,y in zip(Xi,Yi): #zip(Xi,Yi)=[(8.19,7.01),(2.72,2.78),...,(3.78,4.05)] 6 ErrorArray+=(y-(k*x+b))**2 7 return ErrorArray 8 9 ###绘制ErrorArray+最低点### 10 from enthought.mayavi import mlab 11 12 #画整个Error曲面 13 k,b=np.mgrid[k0-1:k0+1:10j,b0-1:b0+1:10j] 14 Err=S(k,b) 15 face=mlab.surf(k,b,Err/500.0,warp_scale=1) 16 mlab.axes(xlabel='k',ylabel='b',zlabel='Error') 17 mlab.outline(face) 18 19 #画最低点(即k,b所在处) 20 MinErr=S(k0,b0) 21 mlab.points3d(k0,b0,MinErr/500.0,scale_factor=0.1,color=(0.5,0.5,0.5)) #scale_factor用来指定点的大小 22 mlab.show()
对要点说明如下:
1、为了让最小二乘法求解的结果出现在绘制曲面的范围内,我们以最终leastsq求得的k0、b0为中心创建k向量和b向量。
2、传入S函数的是k向量和b向量mgrid后的结果。
3、S函数中的ErrorArray+=(y-(k*x+b))**2 操作里,k、b皆为矩阵(是k、b向量mgrid后的结果),而x、y皆为常数,故这里的操作实际上是对矩阵的操作。这个ErrorArray就是上面我说的Err矩阵。
4、在绘图时之所以对Err除以500,是因为Err和k、b的差距不是一般的大,直接绘图会导致什么都看不出来。举一个最简单的例子就是比如我们要画个二维直角坐标系下的图,x的取值范围是0~1,y的取值范围是0~1000,而两个坐标轴却都按一个单位△x=△y=0.1来画,想想看结果会成什么样子?
这里也是同样的道理,于是得给Err除以一个大数才能让图像正常显示。
其实matplotlib画三维坐标系下的图会帮你调整到合适,只有Mayavi才会出现这种情况,反正注意一下比例问题就好了。
5、该程序除过绘制Err曲面外,还把(k0,b0)也画出来了,见灰色小球。
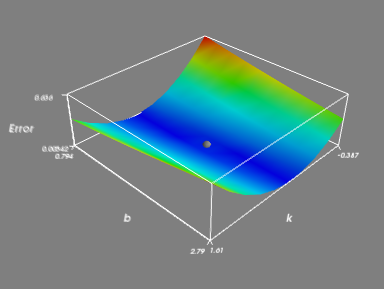
step 6:整个程序的全部代码如下,其中part1与2-1的代码是完全一样的。
1 ###【最小二乘法试验】### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 7 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05]) 8 9 """part 1""" 10 ###需要拟合的函数func及误差error### 11 def func(p,x): 12 k,b=p 13 return k*x+b 14 15 def error(p,x,y): 16 return func(p,x)-y #x、y都是列表,故返回值也是个列表 17 18 p0=[1,2] 19 20 ###最小二乘法求k0、b0### 21 Para=leastsq(error,p0,args=(Xi,Yi)) #把error函数中除了p以外的参数打包到args中 22 k0,b0=Para[0] 23 print"k0=",k0,' ',"b0=",b0 24 25 """part 2""" 26 ###定义一个函数,用于计算在k、b已知时,∑((yi-(k*xi+b))**2)### 27 def S(k,b): 28 ErrorArray=np.zeros(k.shape) #k的shape事实上同时也是b的shape 29 for x,y in zip(Xi,Yi): #zip(Xi,Yi)=[(8.19,7.01),(2.72,2.78),...,(3.78,4.05)] 30 ErrorArray+=(y-(k*x+b))**2 31 return ErrorArray 32 33 ###绘制ErrorArray+最低点### 34 from enthought.mayavi import mlab 35 36 #画整个Error曲面 37 k,b=np.mgrid[k0-1:k0+1:10j,b0-1:b0+1:10j] 38 Err=S(k,b) 39 face=mlab.surf(k,b,Err/500.0,warp_scale=1) 40 mlab.axes(xlabel='k',ylabel='b',zlabel='Error') 41 mlab.outline(face) 42 43 #画最低点(即k,b所在处) 44 MinErr=S(k0,b0) 45 mlab.points3d(k0,b0,MinErr/500.0,scale_factor=0.1,color=(0.5,0.5,0.5)) #scale_factor用来指定点的大小 46 mlab.show()
3 结语
本次博客给出了最小二乘法的Python实现方法,它用到了scipy库中的leastsq函数。在上面我们给出了两个实例,分别实现了对一元一次函数的拟合和一元二次函数的拟合,而事实上,对于函数并不一定得是一元函数,对于更多元的函数也同样能够利用最小二乘法完成拟合工作,不过随着元和次的增加,待求参数也就越来越多了,比方说二元二次函数就有6个待求参数w0~w6。
然为了更好地理解神经网络的训练算法,并不建议直接使用leastsq函数完成对未知参数的求解,因此在以后的博客中我会详细说明如何利用梯度下降法来求解误差函数的最小值。
4 下面要写的博客
1、梯度下降法(什么是梯度下降法,如何使用梯度下降法求一元二次函数最小值,如何使用梯度下降法求二元二次函数的最小值)
2、最小二乘法拟合二元二次函数(即求解w0~w5,相当于对梯度下降法的一个应用)
以上两个内容我会放在同一个博客中。
2016.5.14
by 悠望南山