数据分析练习题

练习 1：图解中国人的生活水平变化

• 你认为应该用什么样的数字来度量中国人的生活水平变化？

先来瞎想下，哪些方面能体现人们的生活水平变化？从物质层面上说，吃饱穿暖了，吃肉喝酒不是问题了，开上车了，开上好车了，住上好房子了，超市、商场物品极大丰富，饭店、宾馆、租车店等各种服务应有尽有，遍地开花，从精神层面上说，电视节目五花八门，无所不包，电影作品层出不穷，网上论坛、博客、微博、微信大大促进了人们的信息分享和交流，极大满足了人们的心理需求，图书市场也是好作品不断，所有这些都能体现人们生活水平的提高，还有从人们的脸色和形体动作所体现出来的精神风貌也能体现出人们生活水平的变化。

那么，如果要用一个数字来度量人们的生活水平变化，应该用什么数字呢？很明显，这个能综合体现生活水平的数字一定不是个简单的数字，这个数字一定是穿透人们生活的表象，抓住了生活水平的本质。

人们生活水平的变化的体现是无微不至，但能用数字来表示的地方还真不多。如果非要用数字，我们第一想到的肯定是工资收入，工资收入能体现生活水平的变化吗？我认为是可以，虽然很单一，但工资收入肯定跟生活水平呈正相关，不管在任何国家，工资收入的变化都能体现出生活水平的变化，当然要扣除通货膨胀等因素。

好了，以我的经济知识水平，也只能想到大家摸着脚趾头都能想到的工资收入了，还是别自己瞎揣摩了，靠谱点的我们还是来看经济学家所用的数字吧。

国际上通用的衡量一个国家公民的生活水平的指标是恩格尔系数。恩格尔系数是指食品支出总额占个人消费支出总额的比重。这个概念很有意思，这个比重能体现人们生活变化的水平。

这是 19 世纪统计学家恩格尔发现的一个规律：一个家庭收入越少，家庭收入中用来购买食物的支出所占比重就越大，随着家庭收入的增加，家庭收入中用来购买食物的比重就下降。也就是说，一个国家或家庭的恩格尔系数越小，说明这个国家或家庭越富裕，反之，恩格尔系数越大，这个国家或家庭的经济越困难。

恩格尔系数在 59% 以上为贫穷，50%-59% 为温饱，40%-50% 为小康，30%-40% 为富裕，低于 30% 为最富裕。

• 尝试找到这样的数据源并画出图看看

数据来自 国家统计局，年度数据——>人民生活——>城乡居民家庭人均收入及恩格尔系数——>时间可选择“1970-2014”，会发现只有 1978 年到 2012年的数据。1979 年的城镇居民家庭恩格尔系数为空，就填补为 1978 和 1980 年的均值。

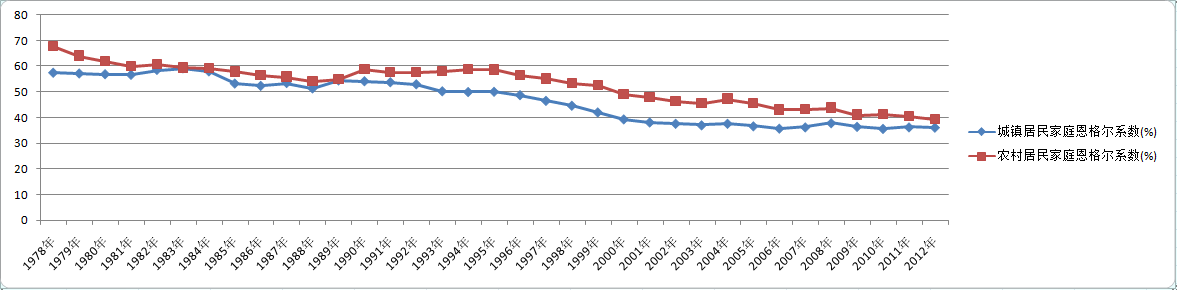
从图中可以看到我国城镇居民家庭恩格尔系数从 1978 年的 57.5% 降到 2012 年的 36.2%，可以说从温饱升为富裕，农村居民家庭恩格尔系数从 1978 年的 67.7% 降到 2012 年的 39.3%，可以说从贫穷升为富裕。

• 用这种数字来衡量有什么样的缺点？

“恩格尔系数”名字不好，不利于传播，不利于群众理解和掌握

练习 2：理解双盲实验

在临床试验中，一方面，如果新药组成员知道自己服的是很可能有用的新药，而对照组病人知道自己吃的是无效的安慰剂，那么仅心理因素就能对两者产生正面或负面的影响；另一方面，研究人员为了得到好结果，有意无意地可能会对新药组病人更精心护理或施加暗示影响病人，在判定疗效时，会更倾向于正面评价新药组病人，更负面评价对照组病人，只收集对新药有利证据而忽视不利证据。为了避免这种偏差，在临床试验中必须遵循“双盲”原则，如果病人不知道但研究人员知道谁服用新药谁服用安慰剂，这是“单盲”，只能解决第一方面问题，要解决后一问题，还需使研究人员也不知道分组情况，如果研究人员和病人都不知道分组情况，就是“双盲”。在双盲情况下，分组情况由第三方人员掌握，医生、护士在“盲态”下给病人使用药物或安慰剂，观察疗效和收集病人的数据，然后把资料交给同样处于“盲态”的数据分析人员去分析。只有最后需要比较新药组和对照组疗效时，才会解除“盲态”，让研究人员和病人知道分组情况。

双盲是避免主观偏差的最好办法。

将世界最聪明的头脑汇聚在一个房间中的 Edge，曾经提过一个有意思的问题：有无数能够增进人们心智能力的科学概念，普通人最应掌握的是什么？ 答：双盲实验。《自私的基因》作者道金斯如是回答，你只需要理解其原则，领悟到为什么有必要这么做，就能感受到其优美。在这些晶体理性促进剂中，或许双盲实验是最重要的，如果每个学校都教学生做，那么会提高我们抵制坏的心智程序的能力。

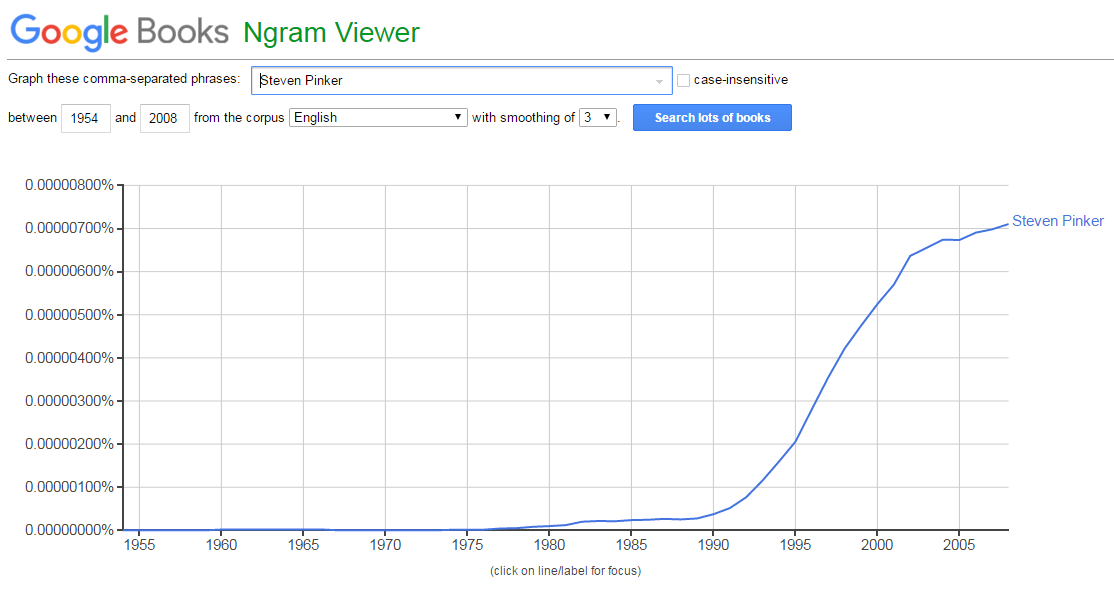
练习 3：学习使用 Google Ngram Viewer

使用 books.google.com/ngrams/ 可以查到某个词从 1800 到 2000 年在出版物中的词频变化，包括英、法、德、俄、西、汉六种文字。

练习 4：理解 Simpson's Paradox

辛普森悖论是指当人们尝试探究两种变量是否具有相关性的时候，会分别对之进行分组研究，在这种研究中，在某些前提下有时会产生在分组比较中都占优势的一方，在总评中反而是失势的一方。

假设有两个大学，P 大和 T 大，两个大学都只有物院和外院，他们的男女人数如下：

物院的数据：

学校	男生人数	女生人数	男女比例
P 大	45	8	5.6
T 大	101	51	2.0

外院的数据：

学校	男生人数	女生人数	男女比例
P 大	50	201	0.25
T 大	9	92	0.1

学校整体数据（即上述两个专业人数之和）：

学校	男生人数	女生人数	男女比例
P 大	95	209	0.45
T 大	110	143	0.77

从以上数据中会发现个很奇怪的现象，物理学院，P 大男女比例大于 T 大，在外院，P 大男女比例大于 T 大，但两个学院加起来整个学校的男女比例，P 大男女比例却小于 T 大！

这里的数据没有错，但人们依然难以接受，难以理解这个悖论。对数据合理性的理解不太容易，但如果能画出合乎数据的几何图形，那就容易让人接受了。

上图中，黑色线表示 P 大数据，红色线表示 T 大数据。Ap 点横坐标为 P 大外院女生人数，纵坐标为 P 大外院男生人数；Bp 点 的横纵坐标则分别为 P 大总女生人数和总男生人数。At 和 Bt 意义与之相对应。

坐标原点为 O，则 OAp 的斜率表示的是 P 大外院的男女比例，ApBp 表示的是 P 大物院的男女比例，OBp 表示的则是 P 大总男女比例；T 大的各线段斜率意义与之对应。

如此以来，这个几何图形就和我们的数据一一对应，在 P 大的外院、物院两个向量的斜率分别大于 T 大的两个向量的斜率的条件下，总人数向量的斜率反而 T 大大。如此直观，合理性毋容置疑。

这里用几何图形从直观上证明了悖论的合理性，但人们依然存在疑问：这是为什么啊？

可以看到，虽然在 P 大不管物院，还是外院，男女比例都比 T 大高一些，但总数比例依然没有 T 大高，很明显，P 大各院的男女比例没有对总比例做出应有的贡献，这跟男生的人数分布是有关系的。这里不再拉拉杂杂耗费大家脑力，但有一个一目了然的例子可以帮助大家理解我在说什么，见下例。

有甲乙两个班，每个班里的学生都分为好生和差生2类，甲班的好生平均分是90分，乙班的好生平均分是95分，乙班高；甲班的差生平均分是60分，乙班的差生平均分是65分，也是乙班高。但是甲班的总体平均分却比乙班高，为什么呢？因为甲班好生比例比乙班高啊（比如甲班50个好生，20个差生，乙班20个好生，50个差生）。

练习 5：利用贝叶斯定理解题

• 已知某种疾病的发病率是0.001，即1000人中会有一个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

贝叶斯公式为：

[P(B_{i}|A)=frac{P(AB_{i})}{P(A)}=frac{P(B_{i})P(A|B_{i})}{sumlimits_{j}P(B_{j})P(A|B_{j})}) ]

本题中的概率为：

P(阳性|得病)=0.99，P(阴性|得病)=0.01，

P(阳性|没得病)=0.05，P(阴性|没得病)=0.95

记 B1={得病}，B2={没得病}，A={阳性}

P(B1)=0.001，P(B2)=0.999

p(A|B1)=0.99，P(A|B2)=0.05

我们要求的是 P(B1|A)

[P(B_{1}|A)=frac{(0.001)(0.99)}{(0.001)(0.99)+(0.999)(0.05)}=0.0194approx0.02) ]

可以看出，即使检测结果为阳性，确实得病的可能性竟然只有 2%，也就是说，测出 100 个人是阳性，那真正得病的可能只有 2 个！要这试剂何用~！准确率太低了嘛！但它的准确率不是 0.99 吗？怎么回事？

这个例子对于不懂贝叶斯的人来说，绝对是难以置信的。上面我们是通过贝叶斯法则算出了精确答案，其实只要进行一些逻辑推理，就能明了基础概率对概率预估结果产生的巨大影响。

由于该疾病得病率极低，1000 人中只有 1 名病人，其试剂准确率为 0.99，这个检测出来应该没问题，但由于试剂的误诊率为 0.05，所以，在其它 999 个健康人中大约会有 50 人被检测为阳性，所以，在检测结果为阳性的 51 个病人中，只有 1 个真正得病的，其它 50 人都是误报。这个问题的基础概率是：绝大多数人都并未得病。患者数量极少的事实 0.001 结合假阳性的概率 0.05，结果就是检测结果为阳性的个体中真正患者的绝对数量其实很少。

不懂概率的人可能会这样推理：由于不得病时检测出阳性的机会才 0.05，我现在呈阳性，说明我有 1-0.05=0.95 的机会带菌。事实当然并非如此。

参考资料：

• 恩格尔系数
• 理性：重新定义人类认知能力 ——《超越智商》推荐序
• 《概率论与数理统计》，陈希孺编著
• 《超越智商，为什么聪明人也会做傻事》
• Simpson's Paradox
• 辛普森悖论：诡异的男女比例
• https://www.zhihu.com/question/22459959