算法导论 第二部分——排序和顺序统计量

一、堆排序 : 原址排序 复杂度： nlg n

最大堆： A[parent(i)] > = A[i]

最小堆： A[parent(i)] < = A[i]

除了最底层外，其它层都是满状态。

判断节点是否为叶节点:  [n/2]+1,.....n 均为叶节点

//Max-heapify（A，i）   ： A为一个 假定 left（i） right(i)的二叉树都是最大堆 。 但是A[i]可能小于孩子  。 时间复杂度为： o(h)
//build_max_heap(A,len) ： 将一个数组转换为 最大堆(从底向上的建堆) ， 时间复杂度为： o（n）
//heap_sort(A,len)      ： 将 A 进行排序  复杂度 为 nlg（n）
void max_heapify(int *A , int i,int len)
{
        int r = RIGHT(i);
        int l = LEFT(i);
        int large = i;
        if (i <= len&&*(A + i-1) < *(A+r-1))
            large = r;
        if (i <= len && *(A+large-1)<*(A+l-1))
            large = l;
        if (large == i)
            return;
        else
            swap(A, large-1, i-1,len);
        if (i <= len && 2 * i < len/2+1)    // decide if  the left son node is leaf node 
            max_heapify(A, large, len);     // not leaf node , carry on the recursion 
        else
            return;                            // end the recursion
}

void build_max_heap(int *A, int len)
{
    for (int i = len / 2; i>0; i--)
        max_heapify(A,i,len);
}

void heap_sort(int *A, int len)
{
    build_max_heap(A,len);
    for (int i = len; i > 0; i--)
    {
        swap(A, i - 1, 0 ,len);
        max_heapify(A,1,i);
    }
}

二、快速排序   原址

最坏时间复杂度： n^2 ,但是是实际应用中最好的排序算法，期望时间复杂度：nlgn，而且隐藏的因子特别小。

// partition();     将数组A[p,……,r] 分成 A[p,….,q-1]<=A[q]<=A[q+1,r]，返回q的数组下标
// quick_sort() :   递归调用，将分割好的数组继续分割
int  PARTITION(int *A ,int p , int r ,int len)
{
    if (p >= len || r >= len|| p<0||r<=0)
    {
        cout << "function PARTITION erro : the p or r is out range of the vector or array" << endl;
        return 0;
    }
    int i = p - 1;
    int x = 0;
    for (int j = p; j < r; j++)
    {
        if (*(A+j)<*(A+r))
        {
            i = i + 1;
            EXCHANGE(A,i,j,len);
        }
    }
    EXCHANGE(A,r,i+1,len);
    return i + 1;
}
void QUICK_SORT(int *A,int p,int r,int len)
{
    if (p >= r)
    {
        cout << "function QUICK_SORT error : r must larger than p" << endl;
        return;
    }
    if (p >= len || r >= len||p<0||r<=0)
    {
        cout << "function QUICK_SORT error : the p or r is out range of the vector or array" << endl;
        return;
    }
    if (p == r)
    {
        cout << "end of calling of QUICK_SORT" << endl;
        return;
    }
    int mid=PARTITION(A,p,r,len);
    cout << "mid is :" << mid << "    p ="<<p<<"    r="<<r<<"    len="<<len<<endl;
    QUICK_SORT(A,p,mid-1,len);
    QUICK_SORT(A,mid+1,r,len);
    output(A,len);
}

performance：

　　worst situation: 

　　　　T(n) = T(n-1) + k;  它的复杂度为 n^2 ，当数组已经是排好序的，那么他需要进行  n^2 次运算

　　best situation: 

　　　　T(n) = 2T(n/2)+k;  当两个子问题的规模都不大于n/2，这时候快速排序的性能最好  nlg n次运算

平衡的划分： 

　　只要每次划分是一种常数比例的划分，都会产生深度为lgn的递归树

　　例如： T(n) = T(n/10)+T(9n/10) + k;

quicksort using random function

RANDOMIZED-PARTITION(A, p, r):
    i = RANDOM(p, r )
    exchange A[r ] ↔ A[i ]
    return PARTITION(A, p, r )

三、线性时间排序

1、 决策树模型：

　　每次比较判断可以影响下一次的比较，

定理:对于一个比较排序算法在最坏情况下，都需要做Ω(nlgn)次比较。

参考： http://www.cnblogs.com/Anker/archive/2013/01/25/2876397.html

2、计数排序 : 时间复杂度为n ,其实是max-min+1，需要额外开辟内存空间

前提条件： 所有的元素都必须在一个范围内，如：  min<a[i]<=max

int * count_sort(int *a ,int n){
    //initialize 
     int max=0xffffffff, min=0x7fffffff;
     for (int i = 0; i < n; i++){
         if (*(a + i)>max)
             max = *(a+i);
         if (*(a + i) < min)
             min = *(a + i);
     }
     const int len = max - min+1;
     int *c = new int[len];
     int *re = new int[n];
     memset(c,0,len*4);

     //count the number of every element in a[] then store in c[]
     for (int i = 0; i < n; i++){
         *(c + *(a+i) - min) += 1;
     }
     //sort based c[] 
     for (int i = 0,j=0; i < len; i++){
         int k = 0;
         while (k < *(c + i)){
             *(re + j) = min + i;
             j++;
             k++;
         }
     }
     delete []c;
     return re;
}

四：中位数和顺序统计量

1、期望为线性时间的选择算法： 最坏时间为n^2

RANDOMIZED_SELECT(A,p,r,i)
      if p==r
         then return A[p]
//通过partition函数产生q值，与快速排序的partition原理相同
      q = RANDOMIZED_PARTITION(A,p,r)
      k = q-p+1;
      if i==k
         then return A[q]
      else  if i<k
          then return RANDOMIZED_SELECT(A,p,q-1,i)
      else
          return RANDOMIZED_SELECT(A,p,q-1,i-k)

c++代码：

#include <iostream>
#include <ctime>
#include <cstdlib>

using namespace std;

void swap(int* x, int* y)
{
    int temp;
    temp = *x;
    *x = *y;
    *y = temp;
}

inline int random(int x, int y)
{
    srand((unsigned)time(0));
    int ran_num = rand() % (y - x) + x;
    return ran_num;
}

int partition(int* arr, int p, int r)
{
    int x = arr[r];
    int i = p - 1;
    for(int j = p; j < r; j++)
    {
        if (arr[j] <= x)
        {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[r]);
    return ++i;
}

int randomizedpartition(int* arr, int p, int r)
{
    int i = random(p, r);
    swap(arr[r], arr[i]);
    return partition(arr, p, r);
}

int randomizedSelect(int* arr, int p, int r, int i)
{
    if(p == r)
    {
        return arr[p];
    }
    int q = randomizedpartition(arr, p, r);
    int k = q - p + 1;
    if(i == k)
    {
        return arr[q];
    }
    else if(i < k)
    {
        return randomizedSelect(arr, p, q - 1, i);
    }
    else
        return randomizedSelect(arr, q + 1, r, i - k);
}

int main()
{
    int arr[] = {1, 3, 5, 23, 64, 7, 23, 6, 34, 98, 100, 9};
    int i = randomizedSelect(arr, 0, 11, 4);
    cout << i << endl;
    return 0;
}

2、最坏情况为线性时间的选择算法

SELECT算法

　　（1）如果n=1，则select直接返回该值

　　（2）将输入数组的n个元素划分为 n/5组，每组5个元素。且至多只有一个组由剩下的n mod 5个元素组成

　　（3）寻找每个组的中位数，首先对每个组中的元素进行插入排序，然后从排序过的序列中选出中位数

　　（4）对3步中找出的中位数，递归调用select以找出其中位数x（如果有偶数个中位数，根据约定，x是下中位数）

　　（5）如果i=k，则返回x。否则，如果i<k, 则在低区递归调用select以找出第i小的元素。如果i>k，则在高区中找地第（i-k）个最小元素。

SELECT算法通过中位数进行划分，可以保证每次划分是对称的，这样就能保证最坏情况下运行时间为θ(n)。算法的证明过程是采用数学归纳法，大致能看懂(p123)。

举个例子说明此过程，求集合A={32,23,12,67,45,78,10,39,9,58,125,84}的第5小的元素，操作过程如下图所示：

                               

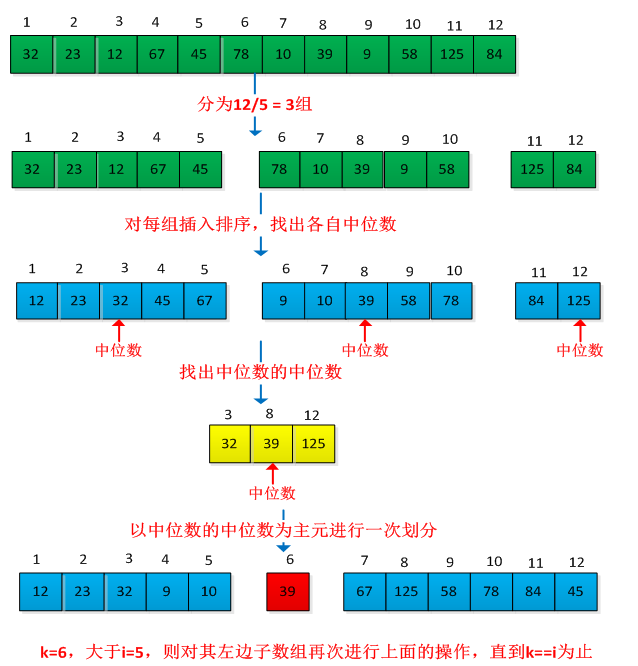
下面c代码和部分内容转自：http://www.cnblogs.com/Anker/archive/2013/01/25/2877311.html

#include <stdio.h>
#include <stdlib.h>

int partition(int* datas,int beg,int last,int mid);
int select(int* datas,int length,int i);
void swap(int* a,int *b);

int main()
{
    int datas[12]={32,23,12,67,45,78,10,39,9,58,125,84};
    int i,ret;
    printf("The array is: 
");
    for(i=0;i<12;++i)
        printf("%d ",datas[i]);
    printf("
");
    for(i=1;i<=12;++i)
    {
       ret=select(datas,12,i);
       printf("The %dth least number is: %d 
",i,datas[i-1]);
    }
    exit(0);
}

int partition(int* datas,int beg,int last,int mid)
{
    int i,j;
    swap(datas+mid,datas+last);
    i=beg;
    for(j=beg;j<last;j++)
    {
        if(datas[j] < datas[last])
        {
            swap(datas+i,datas+j);
            i++;
        }
    }
    swap(datas+i,datas+last);
    return i;
}

int select(int* datas,int length,int i)
{
    int groups,pivot;
    int j,k,t,q,beg,glen;
    int mid;
    int temp,index;
    int *pmid;
    if(length == 1)
        return datas[length-1];
    if(length % 5 == 0)
        groups = length/5;
    else
        groups = length/5 +1;
    pmid = (int*)malloc(sizeof(int)*groups);
    index = 0;
    for(j=0;j<groups;j++)
    {
        beg = j*5;
        glen = beg+5;
        for(t=beg+1;t<glen && t<length;t++)
        {
            temp = datas[t];
            for(q=t-1;q>=beg && datas[q] > datas[q+1];q--)
                    swap(datas+q,datas+q+1);
            swap(datas+q+1,&temp);
        }
        glen = glen < length ? glen : length;
        pmid[index++] = beg+(glen-beg)/2;
    }
    for(t=1;t<groups;t++)
    {
        temp = pmid[t];
        for(q=t-1;q>=0 && datas[pmid[q]] > datas[pmid[q+1]];q--)
            swap(pmid+q,pmid+q+1);
        swap(pmid+q+1,&temp);
    }
   //printf("mid indx = %d,mid value=%d
",pmid[groups/2],datas[pmid[groups/2]]);
    mid = pmid[groups/2];
    pivot = partition(datas,0,length-1,mid);
    //printf("pivot=%d,value=%d
",pivot,datas[pivot]);
    k = pivot+1;
    if(k == i)
        return datas[pivot];
    else if(k < i)
        return select(datas+k,length-k,i-k);
    else
        return select(datas,pivot,i);

}

void swap(int* a,int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}