一、什么是二叉搜索树
二叉查找树是按照二叉树结构来组织的,因此可以用二叉链表结构表示。二叉查找树中的关键字的存储方式满足的特征是:设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]≤key[x]。如果y是x的右子树中的一个结点,则key[x]≤key[y]。根据二叉查找树的特征可知,采用中根遍历一棵二叉查找树,可以得到树中关键字有小到大的序列。
二叉树的查找、最大/小、前驱和后继的伪代码: 复杂度都是 h
//search 递归版 TREE_SEARCH(x,k) if x=NULL or k=key[x] then return x if(k<key[x]) then return TREE_SEARCH(left[x],k) else then return TREE_SEARCH(right[x],k) //search 迭代版 ITERATIVE_TREE_SEARCH(x,k) while x!=NULL and k!=key[x] do if k<key[x] then x=left[x] else then x=right[x] return x //最小指 TREE_MINMUM(x) while left[x] != NULL do x=left[x] return x //最大值 TREE_MAXMUM(x) while right[x] != NULL do x= right[x] return x //后继 TREE_PROCESSOR(x) // 右孩子非空,返回右子树的最小值 if right[x] != NULL then return TREE_MINMUM(right(x)) // 右孩子为空,向上找后继 y=parent[x] while y!= NULL and x ==right[y] do x = y y=parent[y] return y
二叉树的插入和删除 复杂度均为 h
插入和删除会引起二叉查找表示的动态集合的变化,难点在在插入和删除的过程中要保持二叉查找树的性质。插入过程相当来说要简单一些,删除结点比较复杂。
(1)插入
插入结点的位置对应着查找过程中查找不成功时候的结点位置,因此需要从根结点开始查找带插入结点位置,找到位置后插入即可。下图所示插入结点过程:
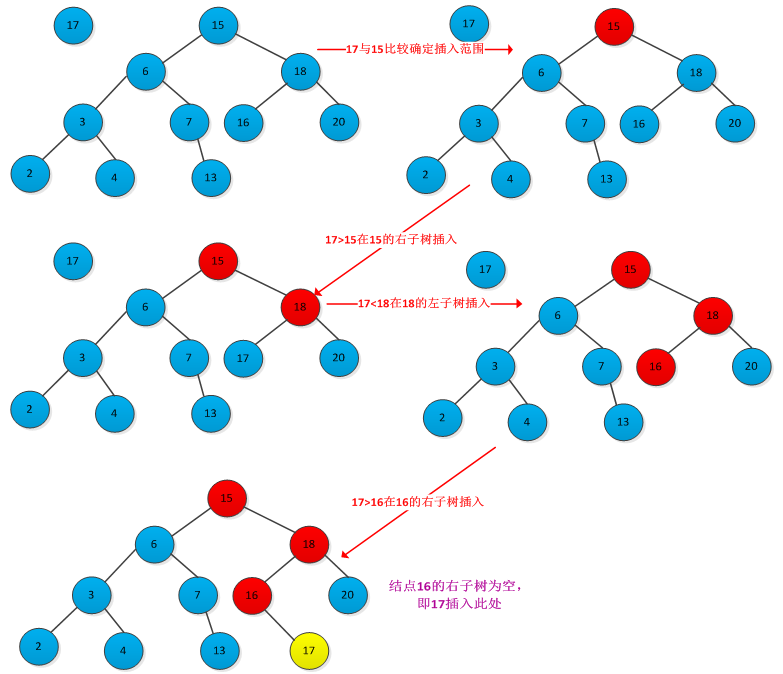
书中给出了插入过程的伪代码:
TREE_INSERT(T,z) y = NULL; x =root[T] while x != NULL do y =x if key[z] < key[x] then x=left[x] else x=right[x] parent[z] =y if y=NULL then root[T] =z else if key[z]>key[y] then keft[y] = z else right[y] =z
(2)删除
从二叉查找树中删除给定的结点z,分三种情况讨论:
<1>结点z没有左右子树,则修改其父节点p[z],使其为NULL。删除过程如下图所示:
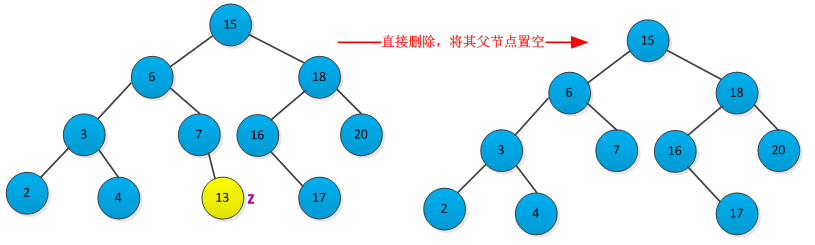
<2>如果结点z只有一个子树(左子树或者右子树),通过在其子结点与父节点建立一条链来删除z。删除过程如下图所示:
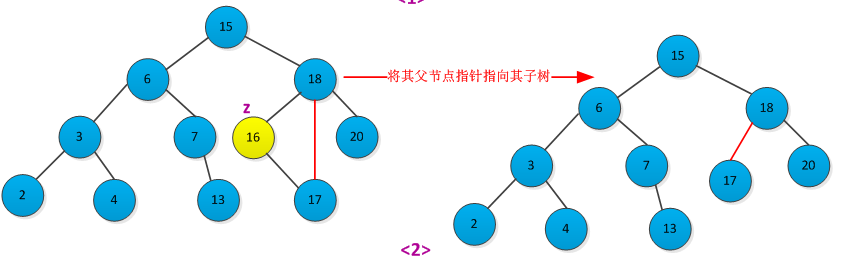
<3>如果z有两个子女,则先删除z的后继y(y没有左孩子),在用y的内容来替代z的内容。
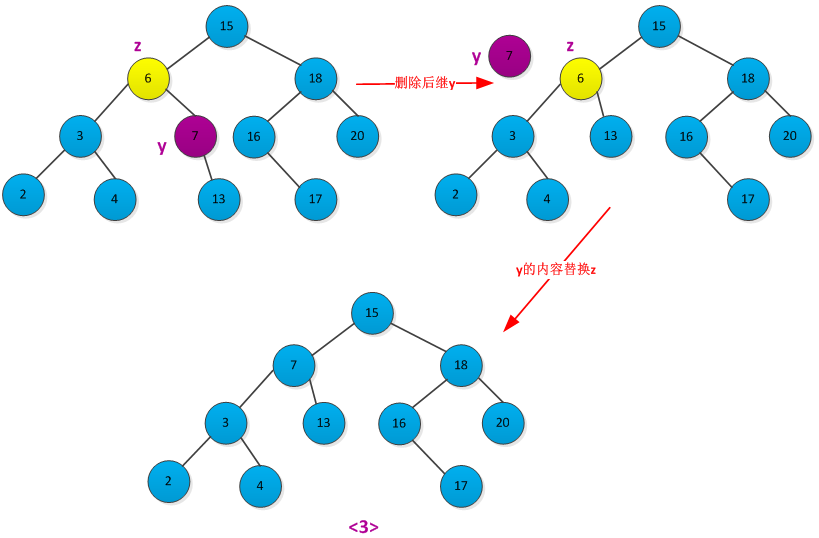
书中给出了删除过程的伪代码:
TREE_DELETE(T,z) if left[z] ==NULL or right[z] == NULL then y=z else y=TREE_SUCCESSOR(z) if left[y] != NULL then x=left[y] else x=right[y] if x!= NULL then parent[x] = parent[y] if p[y] ==NULL then root[T] =x else if y = left[[prarnt[y]] then left[parent[y]] = x else right[parent[y]] =x if y!=z then key[z] = key[y] copy y's data into z return y