作为第二次来纪中，先来受虐一下，莽了一次A组题。
然后爆零了。
这使我充满了决心。
第一眼，组合计数没错了，但不知道怎么下手。
我们考虑:
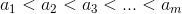这是从原数列中取出m个数。
此时（1<=a<=n）
我们令:
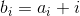
得到：
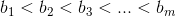
此时（2<=b<=n+m）
显然这些数都是偶数。
因此，最终答案就是在n+m个b中挑出m个偶数的方案数。
用lucas搞一下就能出答案了。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll read(){ 5 ll x=0,f=1; 6 char c=getchar(); 7 while(!isdigit(c)){ 8 if(c=='-') f=-1; 9 c=getchar(); 10 } 11 while(isdigit(c)){ 12 x=(x<<1)+(x<<3)+(c^48); 13 c=getchar(); 14 } 15 return x*f; 16 } 17 const ll N=1e6+10; 18 const ll mod=998244353; 19 ll t,n,m; 20 ll a[N]; 21 ll qp(ll o,ll M){ 22 ll res=o,ans=1; 23 while(M){ 24 if(M&1) ans=(res*ans)%mod; 25 res=(res*res)%mod; 26 M>>=1; 27 } 28 return ans; 29 } 30 ll C(ll n,ll m){ 31 if(m>n) return 0; 32 return (((a[n]*qp(a[m],mod-2))%mod)*qp(a[n-m],mod-2))%mod; 33 } 34 ll lucas(ll n,ll m){ 35 if(!m) return 1; 36 return (lucas(n/mod,m/mod)*C(n%mod,m%mod))%mod; 37 } 38 int main(){ 39 freopen("temple.in","r",stdin); 40 freopen("temple.out","w",stdout); 41 t=read(); 42 a[0]=1; 43 for(int i=1;i<=N;i++) a[i]=(a[i-1]*i)%mod; 44 while(t--){ 45 n=read(); 46 m=read(); 47 printf("%lld ",lucas((n+m)/2,m)); 48 } 49 return 0; 50 }
这道题翻译成简单的话就是，给定一个线段树，在线求覆盖[l,r]的所有子区间需要多少个点（点形式上为一条线段）。
可以考虑一下，对于一个点，有四种情况：
1.这个点的贡献直接就是[x,y]的子区间个数。
2.这里区间经过它的次数就是[x,y]的子区间个数-不与[l,r]有交的部分。
3.这里用到容斥原理，总个数-不相交区间数-完全包含父亲点的区间个数（这里是因为如果直接包含父亲的话，这里就重复计算了）
4.无视即可。
代码以后补上。