嗯...
首先让我们引入高精度这个东西....
相信大家都会做A+B Problem 这道题....输出的是A+B 的值....
可你想过没有,如果A= 5983461827658923256597314923593449492545242655621498167329758256231975822594359252779832914372582828292235591346798922923,
B = 9382872892382859234389628259232359438768953797679368296159683689865328523725925829753298653219197389235498228659659373291973652564256594,
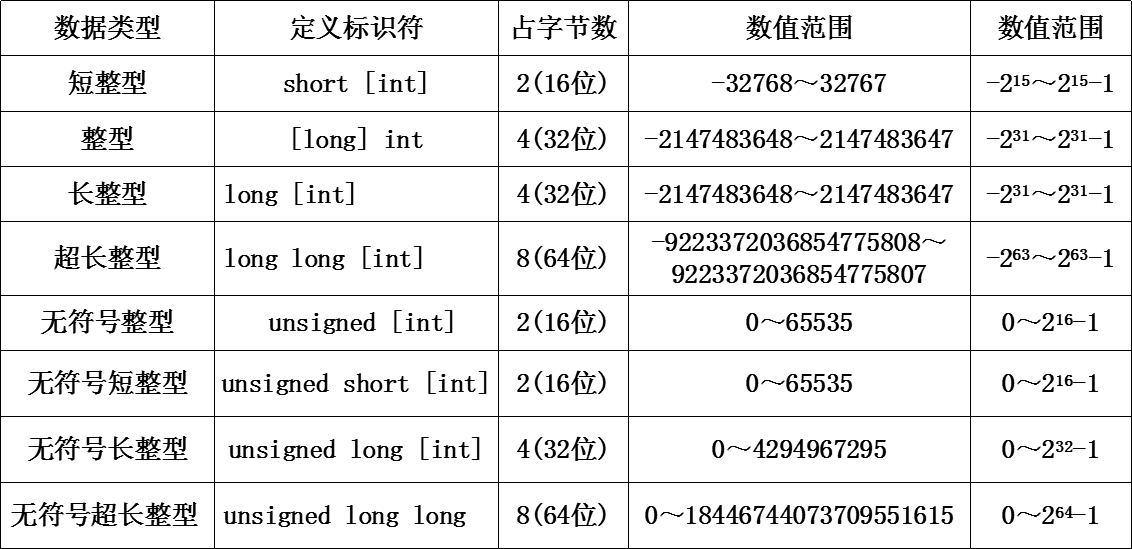
而这时,所有的类型都无法存储A和B这两个数....而这时,高精度就要出马了...(附图关于数据类型范围....
这里首先讲的是高精度的加法。下面是一个伪代码,主要表达了高精度加法的主要流程:

1 read();//读入两个大整数; 2 calsum();//求和; 3 print();//输出结果;
Question 1 :
这么大的数,如何进行读入?
Answer 1:
当输入的数很大时,可采用字符串方式接收。输入要符合整数的输入规则:连续输入每位数字,中间无空格。
在这里会牵扯到另一部分的知识——字符串...其实字符串还是比较常用的...
下面就简单提几方面:
Part 1:
字符串定义方式:
string s; // 直接定义
char s[1007];//用一个字符数组模拟字符串,这种的灵活性与速度上有优势
不同方式定义的字符串,对应的函数也不同
如 string s; len = s.length();
而 char s[1007]; len = strlen(s);
Part 2:
字符串的读入:
这里主要介绍三种方式:1. cin 2.scanf 3.gets
下面给大家演示一下它们的具体的读入方法:
1.cin:

1 string s1,s2; 2 cin>>s1>>s2; 3 int lena = s1.length(); 4 int lenb = s2.length(); 5 6 cout<<s1<<" "<<s2<<endl; 7 cout<<lena<<" "<<lenb;
2.scanf://输入的两个字符串:可以在同一行,中间以空格隔开。也可以各占一行。

1 char s1[1010],s2[1010]; 2 int main() 3 { 4 scanf("%s%s",s1,s2); // scanf("%s%s",&s1,&s2);&可省略 5 int lena=strlen(s1); //strlen()函数需要头文件cstring 6 int lenb=strlen(s2); 7 8 cout<<s1<<" "<<s2<<endl; 9 cout<<lena<<" "<<lenb; 10 }
3.gets://输入的两个字符串必须各占一行

1 char s1[1010],s2[1010]; 2 gets(s1); 3 gets(s2); 4 lena=strlen(s1); 5 lenb=strlen(s2);
注意:
scanf、cin遇空格或回车符则认为当前字符串结束
gets遇回车符则认为当前字符串结束
Question 2:
我们将读入的数作为字符串接收了进来,可是怎么进行加减乘除等数学运算呢?
Answer 2:
拆成一位一位的数字,把它们存在一个数组中,一个数组元素表示一位数字……解释:“拆”
例如:

详细过程:——字符串读入,数组保存(见代码

1 //利用字符串函数和操作运算,将每一位数取出,存入数组中。 2 3 //假设已经利用字符串s读取数据 4 lena=s.length(); //用lena存放字符串s的位数 5 for(i=1;i<=lena;i++) 6 a[i]=s[lena-i] -'0'; //将数串s转换为数组a,注意:倒序存储 7

解释倒序保存的原因:
在平常,数字从左到右依次为从高位到低位....可这里却与日常的习惯相反。因为在存储时我们首先能确定的就是最低位,所以设它为第一位,而高位无法确定,因为在存储之前求出字符串的长度比较麻烦,所以我们用下标较大的数组存储高位,因为它的最高位无法确定....
Question 3:
两个高精度数已经分别保存在数组a和b中,下一步,应该如何求和?
Answer 3:
用到了小学所学的”竖式计算“的思想:
运算的次数为:max(lena, lenb);
程序实现:
方法一:
模拟手工计算,设置一个进位变量m,但是此方式比较麻烦:

1 for (int i=1;i<=lena;i++) 2 a[i]=s1[lena-i]-48;//由字符转向真正意义的数字 ,并且为倒序 3 for (int i=1;i<=lenb;i++) 4 b[i]=s2[lenb-i]-48;//同上 5 lenc = max(lena, lenb); 6 for (int i=1;i<=lenc;i++) 7 { 8 c[i]=(m+a[i]+b[i])%10; 9 m=(m+a[i]+b[i])/10;//进位 10 } 11 if (m) {//判断最高位是否需要进位 12 lenc++; 13 c[lenc]=1; 14 }
方法二:
先计算,最后处理进位,比方法一要简单:

1 for (int i=1;i<=lenc;i++) 2 c[i]=a[i]+b[i];//先计算 3 for (int i=1;i<=lenc;i++) 4 { 5 c[i+1]=c[i+1]+c[i]/10; 6 c[i]=c[i]%10;//后处理进位 7 } 8 if (c[lenc+1]) lenc++;//判断最高位是否需进位
方法三:
方法二的改进,去掉c数组:

1 for (int i=1;i<=lena;i++) 2 a[i]=a[i]+b[i]; //直接加在a数组中 3 for (int i=1;i<=lena;i++) 4 { 5 a[i+1]=a[i+1]+a[i]/10;//进位 6 a[i]=a[i]%10;//保留 7 } 8 if (a[lena+1]) lena++;//特判
最后的问题:
——运算结果的输出:

1 for (i=lenc;i>=1;i--) 2 printf("%d", c[i]); //输出结果 3 printf(" "); 4 5 ============================== 6 7 for (i=lenc;i>=1;i--) 8 cout<<c[i]; //输出结果 9 cout<<endl;
好的,关于高精度的每一个板块已经说明清楚了,下面我们来看一下完整的高精度运算:
(模板============================================================
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 5 using namespace std; 6 7 int a[506], b[506]; 8 int lena, lenb; 9 int m; 10 string a1, b1; 11 12 int main(){ 13 cin>>a1>>b1;//定义的字符串读入只可以用gets和cin,不能用scanf 14 lena = a1.length(); 15 lenb = b1.length(); 16 for (int i = 0; i <= lena - 1; i++){ 17 a[lena - i - 1] = a1[i] -'0'; 18 } 19 for(int i = 0; i <= lenb - 1; i++){ 20 b[lenb - i - 1] = b1[i] - '0'; 21 } 22 if(lena >= lenb){ 23 for(int i = 0; i <= lena - 1; i++){ 24 int ss = a[i]; 25 a[i] = (b[i] + a[i] + m)%10; 26 m = (ss + b[i] + m)/10; 27 } 28 if(m) a[lena] = m; 29 else lena--; 30 for(int i = lena; i >= 0; i--) printf("%d",a[i]); 31 return 0; 32 } 33 else{ 34 for(int i = 0; i <= lenb-1; i++){ 35 int ss = b[i]; 36 b[i] = (b[i] + a[i] + m)%10; 37 m = (ss + a[i] + m) /10; 38 } 39 if(m) b[lenb] = m; 40 else lenb--; 41 for(int i = lenb; i >= 0; i--) printf("%d",b[i]); 42 return 0; 43 } 44 return 0; 45 }
