为了准备面试,早就学习了二叉树,最近想撸一下红黑树。先把二叉树给总结一下吧。
1.二叉树定义
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。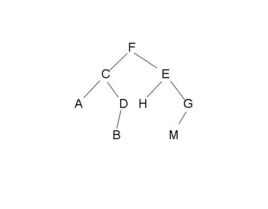
图中就是一个典型的二叉树。
2.二叉树的一些概念
树的结点(node):包含一个数据元素及若干指向子树的分支;
孩子结点(child node):结点的子树的根称为该结点的孩子;
双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
祖先结点: 从根到该结点的所经分支上的所有结点
子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层
结点的度:结点子树的个数
树的度: 树中最大的结点度。
叶子结点:也叫终端结点,是度为 0 的结点;
分枝结点:度不为0的结点;
有序树:子树有序的树,如:家族树;
无序树:不考虑子树的顺序;
----------------回头更新--------
3.二叉树的可视化
要学习二叉树,利用python来构建二叉树,首先要有一个办法能将二叉树可视化。这我找了不少地方,最后不记得在哪找到了一个方法使用networkx和matplotlib来进行绘制。
import networkx as nx import matplotlib.pyplot as plt def create_graph(G, node, pos={}, x=0, y=0, layer=1): pos[node.key] = (x, y) if node.left: G.add_edge(node.key, node.left.key) l_x, l_y = x - 1 / 2 ** layer, y - 1 l_layer = layer + 1 create_graph(G, node.left, x=l_x, y=l_y, pos=pos, layer=l_layer) if node.right: G.add_edge(node.key, node.right.key) r_x, r_y = x + 1 / 2 ** layer, y - 1 r_layer = layer + 1 create_graph(G, node.right, x=r_x, y=r_y, pos=pos, layer=r_layer) return (G, pos) def draw(node): # 以某个节点为根画图 graph = nx.DiGraph() graph, pos = create_graph(graph, node) fig, ax = plt.subplots(figsize=(8, 10)) # 比例可以根据树的深度适当调节 nx.draw_networkx(graph, pos, ax=ax, node_size=600) plt.show()
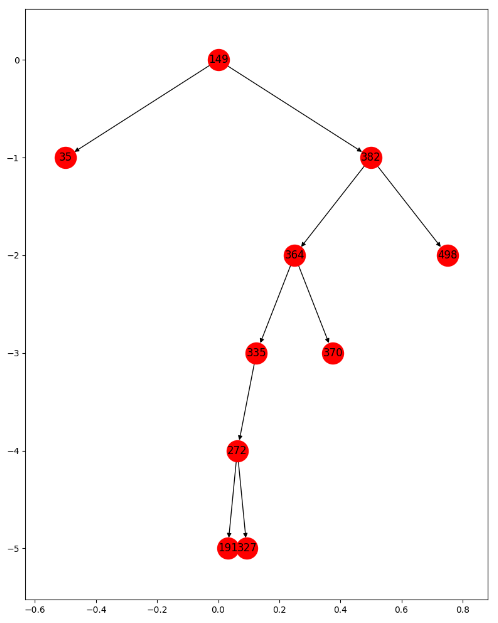
调用的时候,使用draw(tree.root)就可以将整个树绘制出来,如下图所示

4.二叉树的构建
这个没啥好说的,基本就是构建一个节点类作为节点,有左枝和右枝,值,父节点四个属性;还有一个树类,要求要有节点的增,删,查功能。
增:增加一个元素就是从根节点开始,不断对比节点与插入的值,最后找到所在的位置新增一个节点
查:从根节点开始不断向下查找。
删:这个比较麻烦,需要分三种情况讨论:
4.1所删除的节点是叶子节点,直接删除就可以了。
4.2所删除的节点有一个分支,那么就使用它的分支的第一个节点代替它就好了
4.3所删除的节点有两个分支,那么要查找它的最小后继(一定在它的右枝里)然后替换它,再删除原来的最小后继(注意,这个再删除是一个递归过程)
构建代码如下
class node(object): def __init__(self,value): self.key=value self.right=None self.left=None self.parent=None class tree(object): def __init__(self): self.root=None self.nodeArr=[] def add(self,element): newNode=node(element) if self.root: index=self.root lastIndex=index while index!=None: lastIndex = index if index.key <element: index=index.right else : index=index.left if lastIndex.key < element: lastIndex.right=newNode newNode.parent =lastIndex else: lastIndex.left=newNode newNode.parent = lastIndex else: self.root= newNode def find(self,element,root): temp=root while temp: if temp.key<element: temp=temp.right elif temp.key>element: temp=temp.left else: return temp def maxNode(self,node): temp=node while temp.right: temp=temp.right return temp def minNode(self,node): temp=node while temp.left: temp=temp.left return temp def remove(self,element,root): temp=self.find(element,root) print(temp) if temp: newNode=None del_node=temp if temp.right and temp.left:#如果有两个分支 rightMax = self.maxNode(temp) newNode=node(rightMax.key) newNode.parent=del_node.parent del_node.parent.right=newNode newNode.left=del_node.left if del_node.left: del_node.left.parent=newNode newNode.right = del_node.right if del_node.right: del_node.right.parent = newNode del del_node self.remove(newNode.key,newNode.right) elif not temp.right and not temp.left:#没有分支 del_node.parent.right=None del del_node else :#只有一个分支 value=temp.right or temp.left value.parent=del_node.parent if del_node.parent.right.key==temp.key: value.parent.right=value else: value.parent.left=value del del_node
5.整体效果
运行以下代码,可以看到删除节点335前和删除节点335以后的效果。
myTree=tree() s=[149, 382, 364, 335, 35, 498, 370, 272, 327, 191] for i in range(10): myTree.add(s[i]) draw(myTree.root) myTree.remove(335,myTree.root)#删除335节点 draw(myTree.root)