迷宫问题:
问题描述:
存在这样一个迷宫,
int maze[5][5]={
{0,0,0,0,0},
{0,1,0,1,0},
{0,1,1,0,0},
{0,1,1,0,1},
{1,0,0,0,0}
};0 代表可以行进,1 代表不可行进,从起点坐标 (0,0) 出发到终点 (4,4),要求找出一条路。
首先来说第一个思路:
对于起点 (0,0) 它现在有两个方向可以走——向右和向下,至于先走哪一步,看你个人喜好,比如说,我规定让它按照 左,下,右,上 的方向,那它就走到 (1,0) 的位置了,然后继续按照这个规则,一直走到 (3,0),很明显,现在按照这个规则会原路返回,那运行一步到达 (2,0),再次运行程序又会走到 (3,0),因为我们要判断 下,而这个方向是可以的,那就需要我们来解决一个问题,如何让程序知道它已经走过的路并且能够在路走不通的时候回退呢?
我们设立一个标志 di,四个方向对应着不同的值,0—左,1—下,2—右,3—上,在进行各个方向试探的时候,我们设置一个变量 find,初始值设为 0,如果可以走,将 find 设为 1,并且将这个位置标记为 -1,然后进行下一个位置的试探,比如我们进行到 (3,0) ,先把它设为 -1,发现无路可走,我们就将刚才的那个位置 (2,0),从 -1 改为 0,然后继续,先改成-1,此时发现仍然无路可走,我们就只能再将它上面的位置从 -1 改为 0,那么这里又有一个问题,如何让程序知道是改它之前走过的位置,而不是再次按照 左,下,右,上 的方向改呢?
这就要用到数据结构中的栈,我们将走过的路压入栈中(严格地说是走过,并且可以继续走下去的路),如果走投无路,我们就需要先原路返回,即出栈,每回退一步都需要再判断有无其他可走的路,如果没有,则继续回退,直到所有可以走的路都走完。注:压入栈里的数据成员有横坐标纵坐标以及走的方向。
我们手动运行一遍,首先位置 (0,0),判断可走的方向有 1—下(优先,即判断到这里就停止判断了),2—右,(后面将全用数字代替),将其位置标记为 -1,压入栈中,来到 (1,0),判断可走的方向是 1,标记为 -1,压入栈中,来到 (2,0),标记为 -1,压入栈中,来到 (3,0),走投无路,将其位置标记为-1,将栈顶元素 (2,0) 退栈,标记由 -1 改为 0,此时 3 方向可以走(即回溯),以此类推直到 (0,0),此时 (1,0) 已经被设置为 -1,所以可走的方向只剩下 2,然后继续运行,找到终点后,我们将栈中的内容打印出来,最终会得到
这样的输出结果
这个程序只会找到一条路,至于路径长短不做考虑,具体是哪条路这和你定义的判断方向的顺序有关,本例只有一条路,程序如下(为了方便判断我加了边框):
#include<iostream> using namespace std; int maze[5][5]={ {0,0,0,0,0}, {0,1,0,1,0}, {0,1,1,0,0}, {0,1,1,0,1}, {1,0,0,0,0} }; int index[7][7]={ {1,1,1,1,1,1,1}, {1,0,0,0,0,0,1}, {1,0,1,0,1,0,1}, {1,0,1,1,0,0,1}, {1,0,1,1,0,1,1}, {1,1,0,0,0,0,1}, {1,1,1,1,1,1,1} }; typedef struct { int i; int j; int di; }Box; typedef struct { Box data[100]; int top; }Stack; bool DFS(int s1,int s2,int e1,int e2) { int i,j,k,di,find; Stack s; s.top = -1; s.top++; s.data[s.top].i = s1; s.data[s.top].j = s2; s.data[s.top].di = -1; index[s1][s2] = -1; while(s.top>-1) { i = s.data[s.top].i; j = s.data[s.top].j; di = s.data[s.top].di; if(i == e1 && j == e2) { for(k = 0;k <= s.top;k++) { cout<<"("<<s.data[k].i<<","<<s.data[k].j<<")"; if((k+1)%5 == 0) cout<<endl; } cout<<endl; return true; } find = 0; while(di < 4 && find == 0) { di++; switch(di) { case 0: i = s.data[s.top].i-1; j = s.data[s.top].j; break; case 1: i = s.data[s.top].i; j = s.data[s.top].j+1; break; case 2: i = s.data[s.top].i+1; j = s.data[s.top].j; break; case 3: i = s.data[s.top].i; j = s.data[s.top].j-1; break; } if(index[i][j] == 0) find = 1; } if(find == 1) { s.data[s.top].di = di; s.top++; s.data[s.top].i = i; s.data[s.top].j = j; s.data[s.top].di = -1; index[i][j] = -1; } else { index[s.data[s.top].i][s.data[s.top].j] = 0; s.top--; } } return false; } int main(){ if(!DFS(1,1,5,5)) cout<<"no"; return 0; }
接下来看看递归版(同样加了墙,不加墙的做法会在后面说明),这样做的好处是它可以找出所有的路径,我们将迷宫改成如下:
int maze[5][5]={
{0,0,0,0,0},
{0,1,0,1,0},
{0,1,1,0,0},
{0,1,1,0,1},
{0,0,0,0,0}
};判断方法和上面的没有差异,不过递归的原理会让程序试遍所有的方法。程序如下:
#include <iostream> #include <cstdlib> #define N 7 using namespace std; int Maze[N][N] = { {1,1,1,1,1,1,1}, {1,0,0,0,0,0,1}, {1,0,1,0,1,0,1}, {1,0,1,1,0,0,1}, {1,0,1,1,0,1,1}, {1,0,0,0,0,0,1}, {1,1,1,1,1,1,1} }; class Node { public: int data1,data2; Node *next; Node(){this->next = NULL;} Node(int data1,int data2,Node *next) { this->data1 = data1; this->data2 = data2; this->next = next; } }; class Stack { private: Node *top; public: Stack(); bool isEmpty(); void push(int x,int y); void pop(); void Reverse(Stack S); void Output(); Node* getTop(); }; Stack::Stack() { top = NULL; } bool Stack::isEmpty() { return top == NULL; } void Stack::push(int x,int y) { top = new Node(x,y,top); } void Stack::pop() { Node *p = top; top = top->next; delete p; } Node* Stack::getTop() { return top; } void Stack::Reverse(Stack S) { top = top->next; while(!isEmpty()) { S.push(top->data1,top->data2); top = top->next; } S.Output(); } void Stack::Output() { while(!isEmpty()) { if(Maze[top->data1][top->data2] != 0) cout<<"("<<top->data1<<","<<top->data2<<")"<<endl; top = top->next; } } int step[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} }; int count = 0; int Check(int i, int j) { if(i >= 0 && i<=6 && j >= 0 && j <= 6) { if(0 == Maze[i][j]) { return 1; } } return 0; } Stack s; void Find(int s1,int s2) { int n; if(s1 == 5 && s2 == 5) { Stack S; s.Reverse(S); cout<<"(5,5)"<<endl; return; } else { for(n=0; n<4; ++n) { if(Check(s1+step[n][0], s2+step[n][1])) { Maze[s1][s2] = -1; s.push(s1,s2); Find(s1+step[n][0], s2+step[n][1]); Maze[s1][s2] = 0; } } } } int main() { Find(1,1); return 0; }
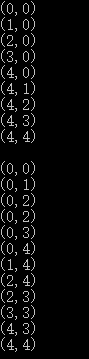
程序运行结果:
如果不想要边框,只需将程序稍作修改,改一下判断范围,起点位置等:
#include <iostream> #include <cstdlib> #define N 5 using namespace std; int Maze[N][N] = { {0,0,0,0,0}, {0,1,0,1,0}, {0,1,1,0,0}, {0,1,1,0,1}, {0,0,0,0,0} }; class Node { public: int data1,data2; Node *next; Node(){this->next = NULL;} Node(int data1,int data2,Node *next) { this->data1 = data1; this->data2 = data2; this->next = next; } }; class Stack { private: Node *top; public: Stack(); bool isEmpty(); void push(int x,int y); void pop(); void Reverse(Stack S); void Output(); Node* getTop(); }; Stack::Stack() { top = NULL; } bool Stack::isEmpty() { return top == NULL; } void Stack::push(int x,int y) { top = new Node(x,y,top); } void Stack::pop() { Node *p = top; top = top->next; delete p; } Node* Stack::getTop() { return top; } void Stack::Reverse(Stack S) { top = top->next; while(!isEmpty()) { S.push(top->data1,top->data2); top = top->next; } S.Output(); } void Stack::Output() { while(!isEmpty()) { if(Maze[top->data1][top->data2] != 0) cout<<"("<<top->data1<<","<<top->data2<<")"<<endl; top = top->next; } } int step[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} }; int count = 0; int Check(int i, int j) { if(i >= 0 && i<=4 && j >= 0 && j <= 4) { if(0 == Maze[i][j]) { return 1; } } return 0; } Stack s; void Find(int s1,int s2) { int n; if(s1 == 4 && s2 == 4) { Stack S; s.Reverse(S); cout<<"(4,4)"<<endl; return; } else { for(n=0; n<4; ++n) { if(Check(s1+step[n][0], s2+step[n][1])) { Maze[s1][s2] = -1; s.push(s1,s2); Find(s1+step[n][0], s2+step[n][1]); Maze[s1][s2] = 0; } } } } int main() { Find(0,0); return 0; }
运行结果:
想要打印一个结果也可以,只需将递归终止时的 return,改成 exit(1),运行所需的时间最少的先打印,运行结果: