1、线性空间的定义
设V是一个以α,β,γ,...为元素的非空集合,F是一个数域,在其中定义两种运算,一种叫加法: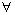 α,β∈V,α+β∈V;另一种叫数量乘法:
α,β∈V,α+β∈V;另一种叫数量乘法: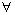 k∈F, α∈V, kα∈V,并且满足下面八条运算法则:
k∈F, α∈V, kα∈V,并且满足下面八条运算法则:
(1)加法交换律:α+β = β+α;
(2)加法结合律:(α+β)+ γ = α+(β+γ);
(3)V中存在零元素: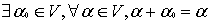 ,记
,记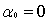 ;
;
(4)负元素存在: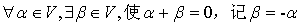 ;
;
(5)数乘结合律: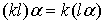 ;
;
(6)存在 ;
;
(7)分配律: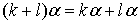 ;
;
(8)分配律: ,
,
则称V为数域F上的线性空间。V中元素称为向量。F为实(复)数域时,称V是实(复)线性空间。
2、欧式空间与酉空间
对数域F上的n维线性空间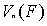 ,定义了一个从
,定义了一个从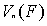 中向量到数域F的二元运算,记为
中向量到数域F的二元运算,记为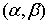 ,即
,即 ,如果满足
,如果满足
(1)对称性: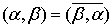 ,其中
,其中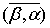 表示复数
表示复数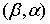 的共轭;
的共轭;
(2)线性性:

(3)正定性: 的充要条件是
的充要条件是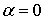
则称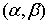 是
是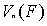 的一个内积,并称其中定义了内积的线性空间
的一个内积,并称其中定义了内积的线性空间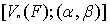 为内积空间。
为内积空间。
如果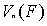 是实数域R上的线性空间
是实数域R上的线性空间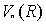 ,则
,则 为实内积,对称性相应为
为实内积,对称性相应为 ,
,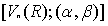 为欧式空间(Euclidean Space)
为欧式空间(Euclidean Space)
同理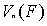 是复数域C上的线性空间
是复数域C上的线性空间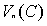 时,
时,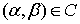 为复内积,称
为复内积,称 为酉空间(Unitary Space)。
为酉空间(Unitary Space)。
以下摘录自知乎:
欧氏空间可以理解为几何空间的度量性在线性空间推广的结果。
线性空间缺乏度量性,不能在线性空间上描述向量的长度及向量间的夹角,这一不足制约了线性空间的使用。参考几何空间,向量的长度及向量间的夹角在几何空间都能通过向量的内积来定义,因此只要在线性空间加入内积这一运算,就能让线性空间具有度量性。
对几何空间的内积进行抽象,可知其本质为几何空间到实数域的一个二元映射,且这种映射具有对称性、左线性及正定性。于是,做下述定义。
欧氏空间:设A是一个实数域上的线性空间,定义一个A到实数域R的二元映射f,使得A中任意两个向量在R中都有唯一确定的数与之对应,若f满足以下三点:
任意α、β、γ∈A,任意k、l∈R
(1)f(α, β) = f(β, α) ;(对称性)
(2)f(kα + lβ, γ) = kf(α, γ) + lf(β, γ) ;(左线性)
(3)当α ≠ 0时,f(α, α) >0;(正定性)
则称f为A的内积,A就称为欧氏空间。简而言之,欧氏空间就是具有了内积的线性空间。
作者:董玄析
链接:https://www.zhihu.com/question/27903807/answer/262893650
来源:知乎