C. Primes or Palindromes?

prime numbers non greater than n is about .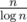

We can also found the amount of palindrome numbers with fixed length k — it is about 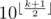 which is .

#include <iostream>
#include <cstdio>
#include <string.h>
#include <cmath>
using namespace std;
const int maxn=2000006;
typedef long long LL;
int numPrime[maxn],numpalindrome[maxn];
void sieve()
{
    int na=1000000*2;
    int m=sqrt(na+1);
    for(LL i=2; i<=m; i++)if(numPrime[i]){
       for(LL j=i*i; j<=na; j+=i) numPrime[j]=0;
    }

}
int a[15];
int jud(int n)
{
    int t=n,m=0;
    while(t)
        m=m*10+t%10,t/=10;
    return n==m;
}
int main()
{
   for(int i=2; i<maxn; i++)numPrime[i]=1;
   sieve();
   for(int i=3; i<maxn; i++)numPrime[i]+=numPrime[i-1];
   for(int i=1; i<maxn; i++)numpalindrome[i]+=jud(i)+numpalindrome[i-1];
   int p,q;
   while(scanf("%d%d",&p,&q)==2)
    {
          int ans=-1;
           for(int i=1; i<=2000000; i++)
            if(numPrime[i]*q<=numpalindrome[i]*p)ans=i;
            if(ans==-1) puts("Palindromic tree is better than splay tree");
            else printf("%d
",ans);
    }
    return 0;
}