频繁项集算法

基础知识：

用户	薯片(A)	可乐(B)	铅笔(C)	羽毛球(D)	洗衣液(E)
1	√	√		√
2	√		√	√	√
3	√	√		√
4		√	√	√
5	√		√

支持度：单个项占总项集的百分比，比如薯片的支持度=4/5*100%=80%，可乐的支持度=3/5*100%=60%。

置信度：薯片=>羽毛球的置信度=3/4*100%=75%，可乐=>羽毛球的置信度=3/3*100%=100%。

一、Apriori算法

假设minsupport=0.2，得出频繁项集：

1）1-项集C1={A，B，C，D，E}，1-频繁项集L1={A，B，C，D}；

2）1-频繁项集进行拼接得到2-项集C2={(A,B)，(A,C)，(A,D)，(B,C)，(B,D)，(C,D)}，2-频繁项集L2={(A,B)，(A,C)，(A,D)，(B,D)，(C,D)}

3）2-频繁项集拼接得到3-项集C3={(A,B,C)，(A,B,D)，(A,C,D)，(B,C,D)}，3-频繁项集L3={(A,B,D)}

4）最后得到所有的频繁项目集L={(A,B)，(A,C)，(A,D)，(B,D)，(C,D)，(A,B,D)}

假设minconfidence=60%，得出关联规则：

我们这里仅仅对最大的频繁项集(B,C,D)进行计算，得出其中是否有强关联规则：

B=>CD，confidence=33%，不是强关联规则；BC=>D，confidence=100%，强关联规则；

C=>BD，confidence=33%，不是强关联规则；CD=>B，confidence=50%，不是强关联规则；

D=>BC，confidence=25%，不是强关联规则；BD=>C，confidence=33%，不是强关联规则。

二、FP-Tree算法

1）我们仍然选用上面的例子，用户1：ABD，用户2：ACDE，用户3：ABD，用户4：BCD，用户5：AC

第一次扫描数据对1-项集进行计数：

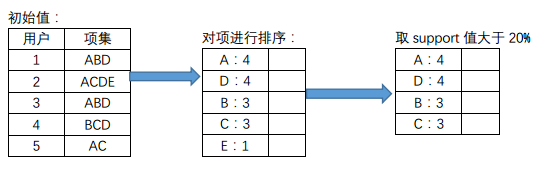
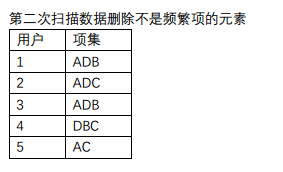
2）建立FP-Tree

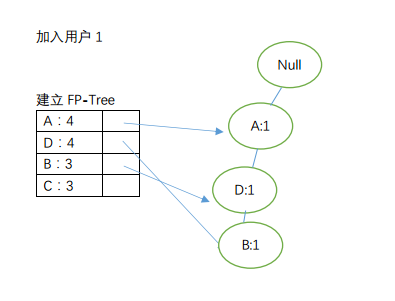
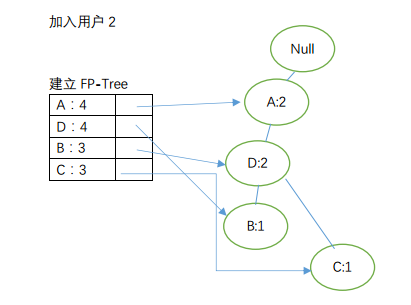
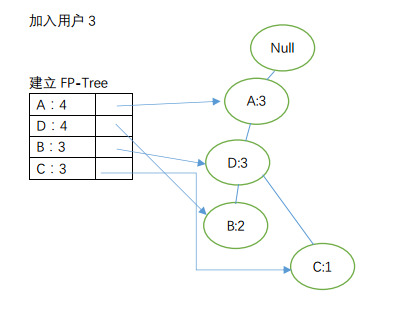
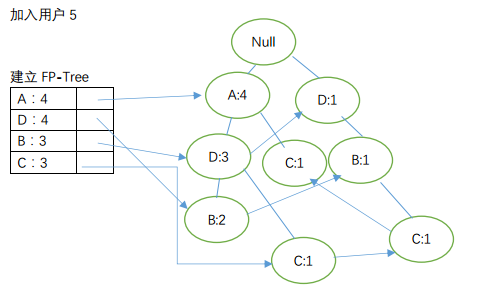
至此，我们完成对FP-Tree的构建。

3）FP-Tree获取频繁项集

   由节点从下到上依次获取频繁项：

   

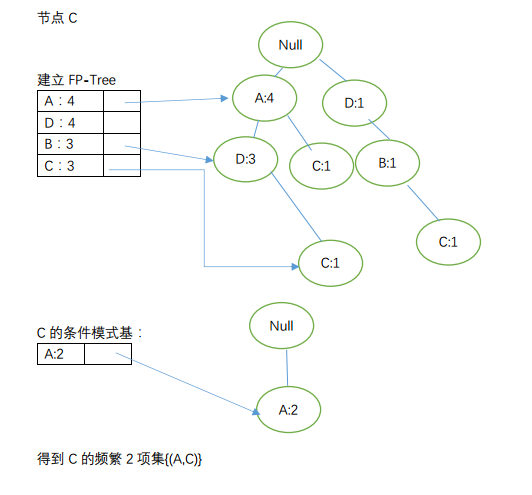
       其实上述中{(C,D)}的FP-Tree分别出现了2次，我们可得出其为频繁2-项集，则有C的到的频繁项2-项集：{(A,C)，(C,D)}；

     

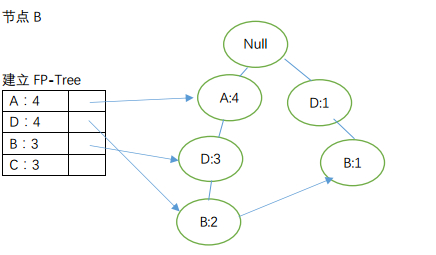
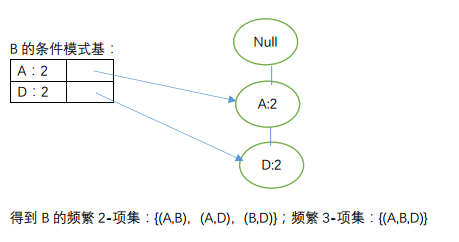
  节点D

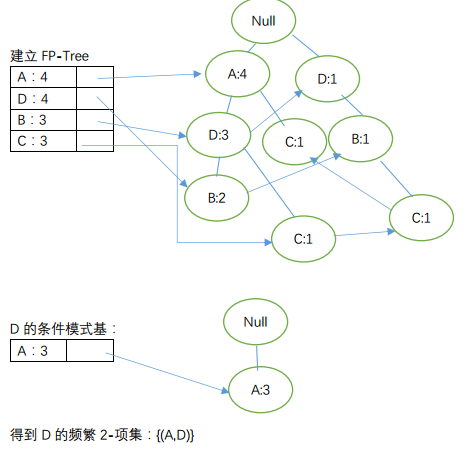
   综上可知，所有的频繁项为：{(A,B)，(A,C)，(A,D)，(B,D)，(C,D)，(A,B,D)}。