20172303 2018-2019-1《程序设计与数据结构》深度优先遍历
遍历
- 图的遍历是指从图中的某一顶点出发,按照一定的策略访问图中的每一个顶点。当然,每个顶点有且只能被访问一次。
- 在图的遍历中,深度优先和广度优先是最常使用的两种遍历方式。这两种遍历方式对无向图和有向图都是适用的,并且都是从指定的顶点开始遍历的。
深度优先遍历
简单介绍
- 深度优先遍历也叫深度优先搜索(Depth First Search)。
- 遍历规则:不断地沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。具体点,给定一图G=<V,E>,用visited[i]表示顶点i的访问情况,则初始情况下所有的visited[i]都为false。假设从顶点V0开始遍历,则下一个遍历的顶点是V0的第一个邻接点Vi,接着遍历Vi的第一个邻接点Vj,直到所有的顶点都被访问过。
- 所谓的第一个是指在某种存储结构中(邻接矩阵、邻接表),所有邻接点中存储位置最近的,通常指的是下标最小的或元素最小的。
遍历过程
- 在遍历的过程中有两种情况经常出现:
- 某个顶点的邻接点都已被访问过的情况,此时需回溯已访问过的顶点。
- 图不连通,所有的已访问过的顶点都已回溯完了,仍找不出未被访问的顶点。此时需从下标0开始检测visited[i],找到未被访问的顶点i,从i开始新一轮的深度搜索。
- 举个例子
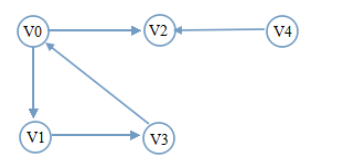
- V0->V1->V3->V2->V4
- V1->V3->V0->V2->V4
- V2->V0->V1->V3->V4
- V3->V0->V1->V2->V4
- V4->V2->V0->V1->V3
代码分析
- 深度优先遍历——使用一个栈和一个无序列表来实现,栈用于管理遍历,无序列表用于存储遍历结果
- 第一步:起始顶点进入栈。
- 第二步:从栈中取出起始顶点加入无序列表的末端,标记为已访问,让与该顶点相连的顶点加入栈中。
- 第三步:重复第二步的操作,每次取出栈顶元素加入无序列表,把顶点标记为已访问,直至栈为空。
- 邻接矩阵实现的图中的深度优先遍历
public Iterator<T> iteratorDFS(int startIndex)
{
Integer x;
boolean found;
StackADT<Integer> traversalStack = new LinkedStack<Integer>();
UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
boolean[] visited = new boolean[numVertices];// 标记判断是否访问,防止出现重复遍历的情况
if (!indexIsValid(startIndex)) {
throw new ElementNotFoundException("Graph");
// return resultList.iterator();
}
// numVertices用于记录顶点的个数
for (int i = 0; i < numVertices; i++) {
visited[i] = false;
}
traversalStack.push(new Integer(startIndex));
resultList.addToRear(vertices[startIndex]);
visited[startIndex] = true;
// 开始循环,每次把栈顶元素添加到resultList中,将与首顶点连接的还未进入队列的顶点加入栈
while (!traversalStack.isEmpty())
{
x = traversalStack.peek();
found = false;
//找到一个与x相邻的没有访问过的顶点,并将其入栈
for (int i = 0; (i < numVertices) && !found; i++)
{
if (adjMatrix[x.intValue()][i] && !visited[i])
{
traversalStack.push(new Integer(i));
resultList.addToRear(vertices[i]);
visited[i] = true;
found = true;
}
}
if (!found && !traversalStack.isEmpty()) {
traversalStack.pop();
}
}
return new GraphIterator(resultList.iterator());
}
public Iterator iteratorBFS(int startIndex){
Integer x;
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
UnorderedListADT resultList = new ArrayUnorderedList();
// 若所给索引值无效,抛出错误
if (!indexIsValid(startIndex)){
throw new ElementNotFoundException("Graph");
}
// 设置每个顶点是否被访问,初始设置为未访问
boolean[] visited = new boolean[numVertices];
for (int i = 0;i < numVertices;i++){
visited[i] = false;
}
// 起始顶点进入队列,并标记为已访问
traversalQueue.enqueue(startIndex);
visited[startIndex] = true;
// 开始循环,每次把队列中的首顶点添加到resultList中,将与首顶点连接的还未进入队列的顶点加入队列,并标记为已访问
while (!traversalQueue.isEmpty()){
x = traversalQueue.dequeue();
resultList.addToRear(vertices.get(x).getElement());
for (int i = 0;i < numVertices;i++){
if (hasEdge(x,i) && !visited[i]){
traversalQueue.enqueue(i);
visited[i] = true;
a++;
}
}
}
return new GraphIterator(resultList.iterator());
}
// 判断两顶点之间是否有边
public boolean hasEdge(int a,int b){
if (a == b){
return false;
}
VerticeNode vertex1 = vertices.get(a);
VerticeNode vertex2 = vertices.get(b);
while (vertex1 != null){
if (vertex1.getElement() == vertex2.getElement()){
return true;
}
vertex1 = vertex1.getNext();
}
return false;
}
一个例子
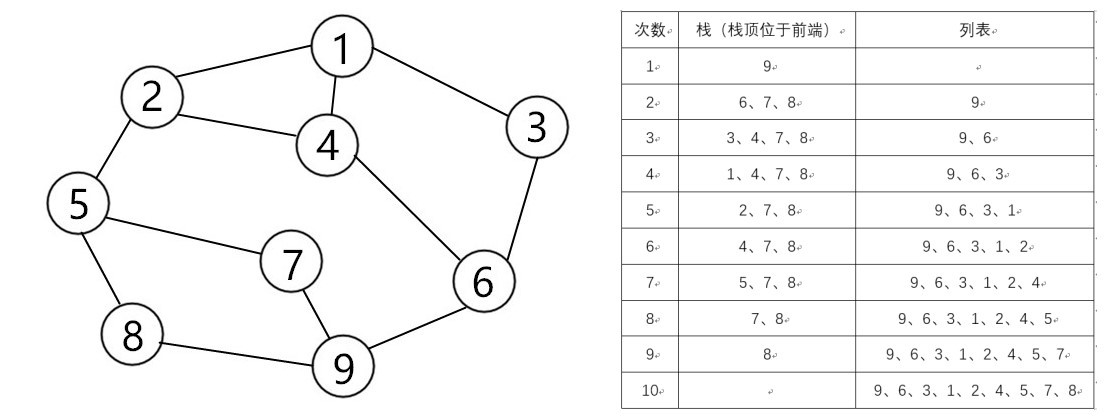
参考资料

