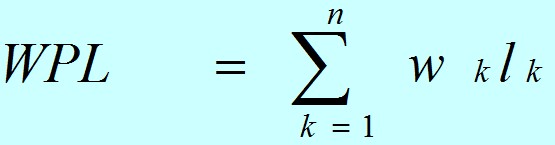20172303 2018-2019-1《程序设计与数据结构》哈夫曼树编码与解码

20172303 2018-2019-1《程序设计与数据结构》哈夫曼树编码与解码

哈夫曼树简介

• 定义：给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
• 带权路径长度（Weighted Path Length of Tree,简记为WPL）
  • 结点的权：在一些应用中,赋予树中结点的一个有某种意义的实数。
  • 结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积。
  • 树的带权路径长度(Weighted Path Length of Tree)：定义为树中所有叶结点的带权路径长度之和。
    

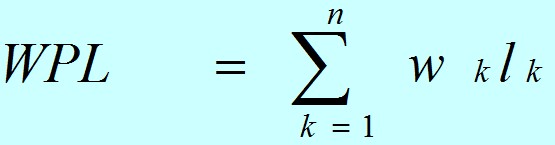
哈夫曼树的构造

• 哈夫曼树并不唯一，但带权路径长度一定是相同的。下面用一个例子来解释哈夫曼树的构造。
• （1）假设有8个结点，其权值大小如下
  
• （2）从中选择最小的两个结点2和3，合成一颗树，根结点的值为两个孩子结点的值相加
  
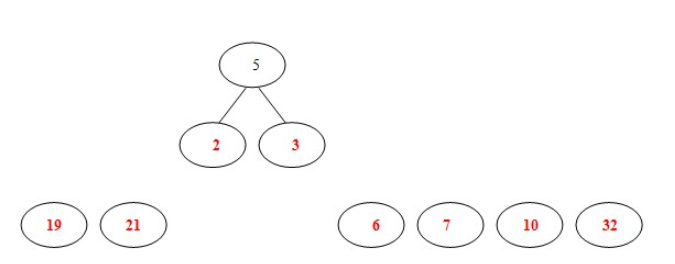
• （3）从剩余的结点（包括新生成的树的根结点）中在选择两个最小的结点5和6，构造新树
  
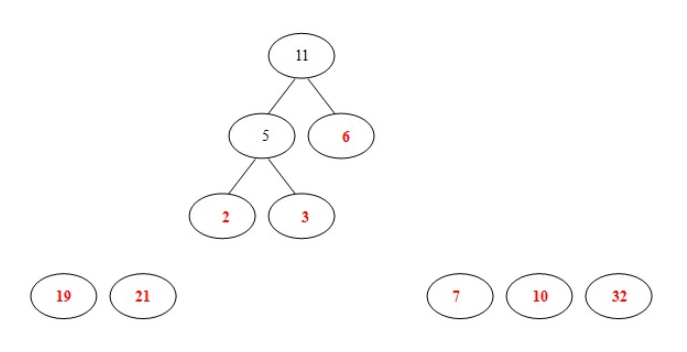
• （4）继续从中进行选择，此时选择7和10，因为这两个结点都和之前生成的树无关，所以他们重新生成一棵树（如果两个数的和正好是下一步的两个最小数的其中的一个，那么这个树直接往上生长就可以了，如果这两个数的和比较大，不是下一步的两个最小数的其中一个，那么就并列生长）
  
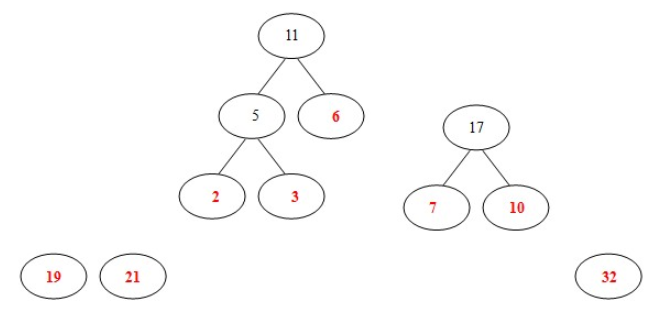
• （5）从19，21，32，11，17中进行选择，选择11和17，构造新树
  
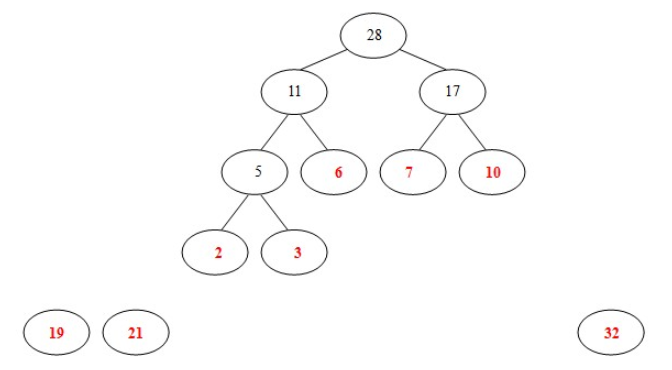
• （6）选择19和21，构造新树
  
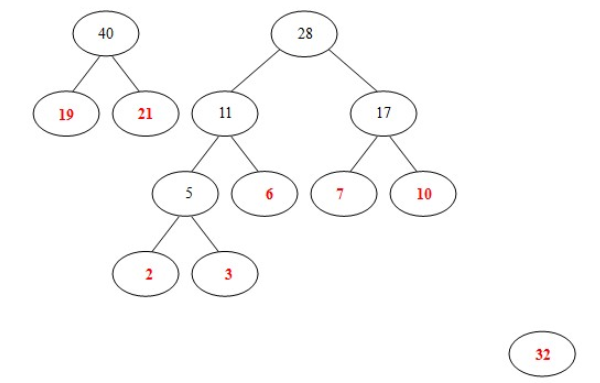
• （7）选择28和32，构造新树
  
• （8）此时只剩下两颗树，将其重新构造一颗新树，一颗哈夫曼树就成型了
  

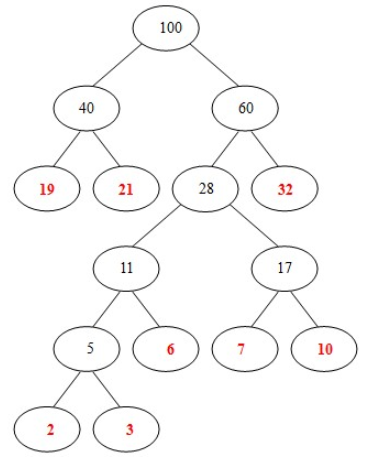
哈夫曼树代码实现

• 代码参考了java创建哈夫曼树和实现哈夫曼编码

HuffmanNode类

• 首先设置一个HuffmanNode类作为实现的基础，每个结点都包含一个六项内容：权值、结点代表字母、字母的编码、左孩子、右孩子和父结点，为了方便之后进行结点的比较，这里还重新编写了一下compareTo方法。

public int compareTo(HuffmanNode<T> o) {
    if (this.getWeight() > o.getWeight()){
        return -1;
    }
    else if (this.getWeight() < o.getWeight()){
        return 1;
    }
    return 0;
}

HuffmanTree类

• 在HuffmanTree类里有两个方法，第一个方法createTree方法用于构造树，第二个方法BFS方法是使用广度优先遍历来给每一个叶子结点进行编码。具体方法及步骤在代码中都已写明。

public static HuffmanNode createTree(List<HuffmanNode<String>> nodes) {
    while (nodes.size() > 1){
        // 对数组进行排序
        Collections.sort(nodes);
        // 当列表中还有两个以上结点时，构造树
        // 获取权值最小的两个结点
        HuffmanNode left = nodes.get(nodes.size() - 2);
        left.setCode(0 + "");
        HuffmanNode right = nodes.get(nodes.size() - 1);
        right.setCode(1 + "");
        // 生成新的结点，新结点的权值为两个子节点的权值之和
        HuffmanNode parent = new HuffmanNode(left.getWeight() + right.getWeight(), null);
        // 使新结点成为父结点
        parent.setLeft(left);
        parent.setRight(right);
        // 删除权值最小的两个结点
        nodes.remove(left);
        nodes.remove(right);
        nodes.add(parent);
    }
    return nodes.get(0);
}

public static List<HuffmanNode> BFS(HuffmanNode root){
    Queue<HuffmanNode> queue = new ArrayDeque<HuffmanNode>();
    List<HuffmanNode> list = new java.util.ArrayList<HuffmanNode>();

    if (root != null){
        // 将根元素加入队列
        queue.offer(root);
        root.getLeft().setCode(root.getCode() + "0");
        root.getRight().setCode(root.getCode() + "1");
    }

    while (!queue.isEmpty()){
        // 将队列的队尾元素加入列表中
        list.add(queue.peek());
        HuffmanNode node = queue.poll();
        // 如果左子树不为空，将它加入队列并编码
        if (node.getLeft() != null){
            queue.offer(node.getLeft());
            node.getLeft().setCode(node.getCode() + "0");
        }
        // 如果右子树不为空，将它加入队列并编码
        if (node.getRight() != null){
            queue.offer(node.getRight());
            node.getRight().setCode(node.getCode() + "1");
        }
    }
    return list;
}

HuffmanMakeCode类

• HuffmanMakeCode类用于将文件中的内容提取，放入数组并进行计数，这里将数组长度设置为27，因为还对空格进行了计数，以便于解码。具体方法及步骤在代码中都已写明。

public class HuffmanMakeCode {
    public static char[] word = new char[]{'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s'
            ,'t','u','v','w','x','y','z',' '};
    public static int[] number = new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};

    public static String makecode(FileInputStream stream) throws IOException {
        //读取文件(缓存字节流)
        BufferedInputStream in = new BufferedInputStream(stream);
        //一次性取多少字节
        byte[] bytes = new byte[2048];
        //接受读取的内容(n就代表的相关数据，只不过是数字的形式)
        int n = -1;
        String a = null;
        //循环取出数据
        while ((n = in.read(bytes, 0, bytes.length)) != -1) {
            //转换成字符串
            a = new String(bytes, 0, n, "GBK");
        }

        // 对文件内容进行计数
        count(a);

        return a;
    }

    // 实现对文件内容计数，内层循环依次比较字符串中的每个字符与对应字符是否相同，相同时计数；外层循环指定对应字符从a至空格
    public static void count(String str){
        for (int i = 0;i < 27;i++){
            int num = 0;
            for (int j = 0;j < str.length();j++){
                if (str.charAt(j) == word[i]){
                    num++;
                }
            }
            number[i] += num;
        }
    }

    public static char[] getWord() {
        return word;
    }

    public static int[] getNumber() {
        return number;
    }
}

HuffmanTest类

• HuffmanTest类进行了文件的读取，构造哈夫曼树，编码，解码，文件的写入五个步骤，其中前三个步骤使用之前三个类中的方法即可实现，这里主要说一下后两个步骤。
• 解码：解码部分使用一个列表list4将编码结果的字符串转化到列表中去，然后定义了两个变量，第一个变量用于每次依次获取的编码值，然后与list3（存储编码的列表）进行比较找到对应索引，然后将list2（存储字母的列表）中对应索引值位置的字母加入第二个变量中，每次循环后删除列表list4的第一个元素，循环直至list4为空时结束，第二个变量temp1中存储的即为解码结果。

// 进行解码
List<String> list4 = new ArrayList<>();
for (int i = 0;i < result.length();i++){
    list4.add(result.charAt(i) + "");
}
String temp = "";
String temp1 = "";
while (list4.size() > 0){
    temp += "" + list4.get(0);
    list4.remove(0);
    for (int i = 0;i < list3.size();i++){
        if (temp.equals(list3.get(i))){
            temp1 += "" + list2.get(i);
            temp = "";
        }
    }
}
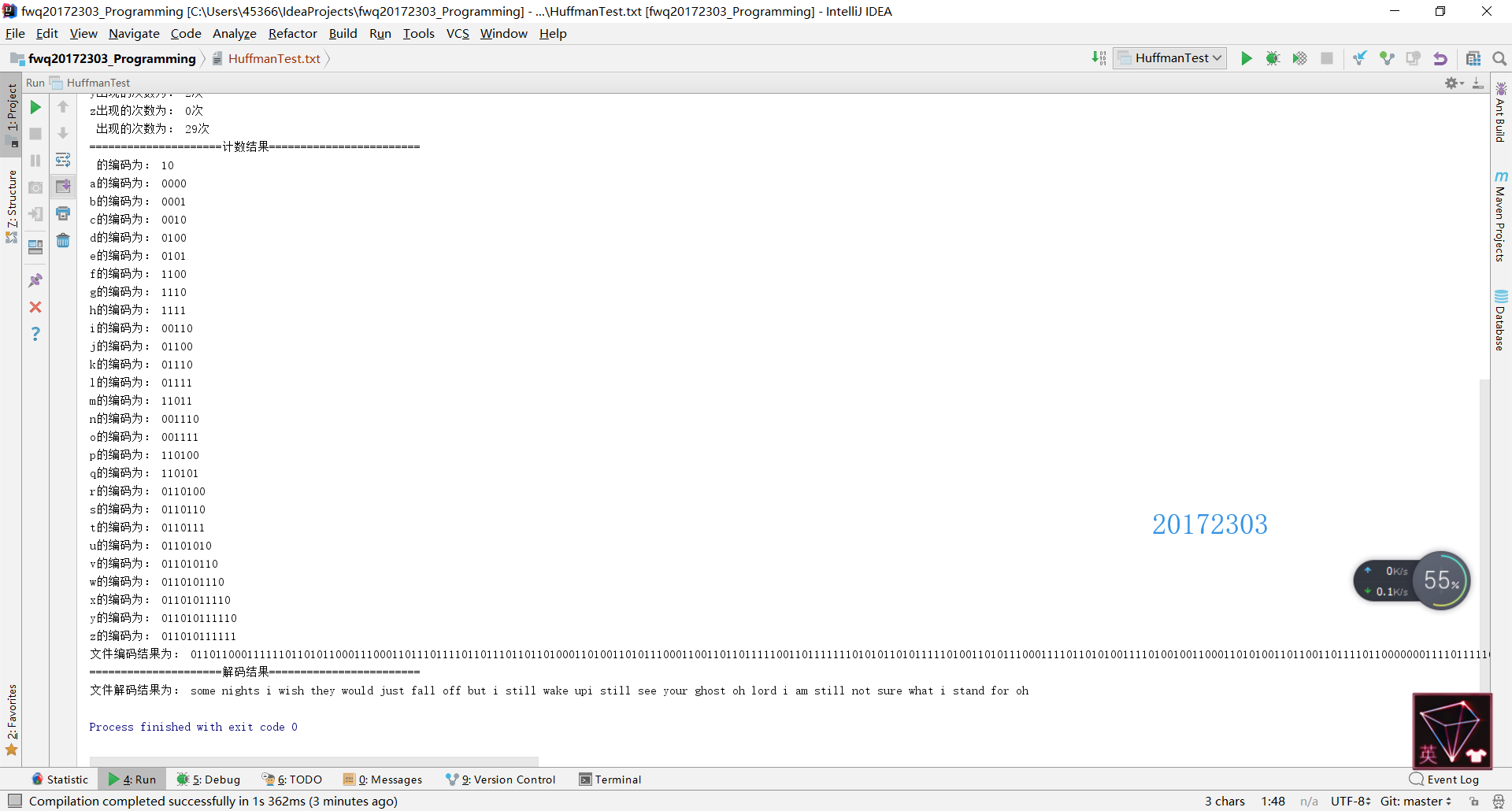
System.out.println("文件解码结果为： " + temp1);

• 文件写入：文件写入就是很简单的方法使用，这里使用的是字符操作流（使用FileWriter类和FileReader类）的方法。

// 写入文件
File file = new File("C:\Users\45366\IdeaProjects\fwq20172303_Programming\HuffmanTest2.txt");
Writer out = new FileWriter(file);
out.write(result);
out.close();

实验结果

• 所读取的文件
  
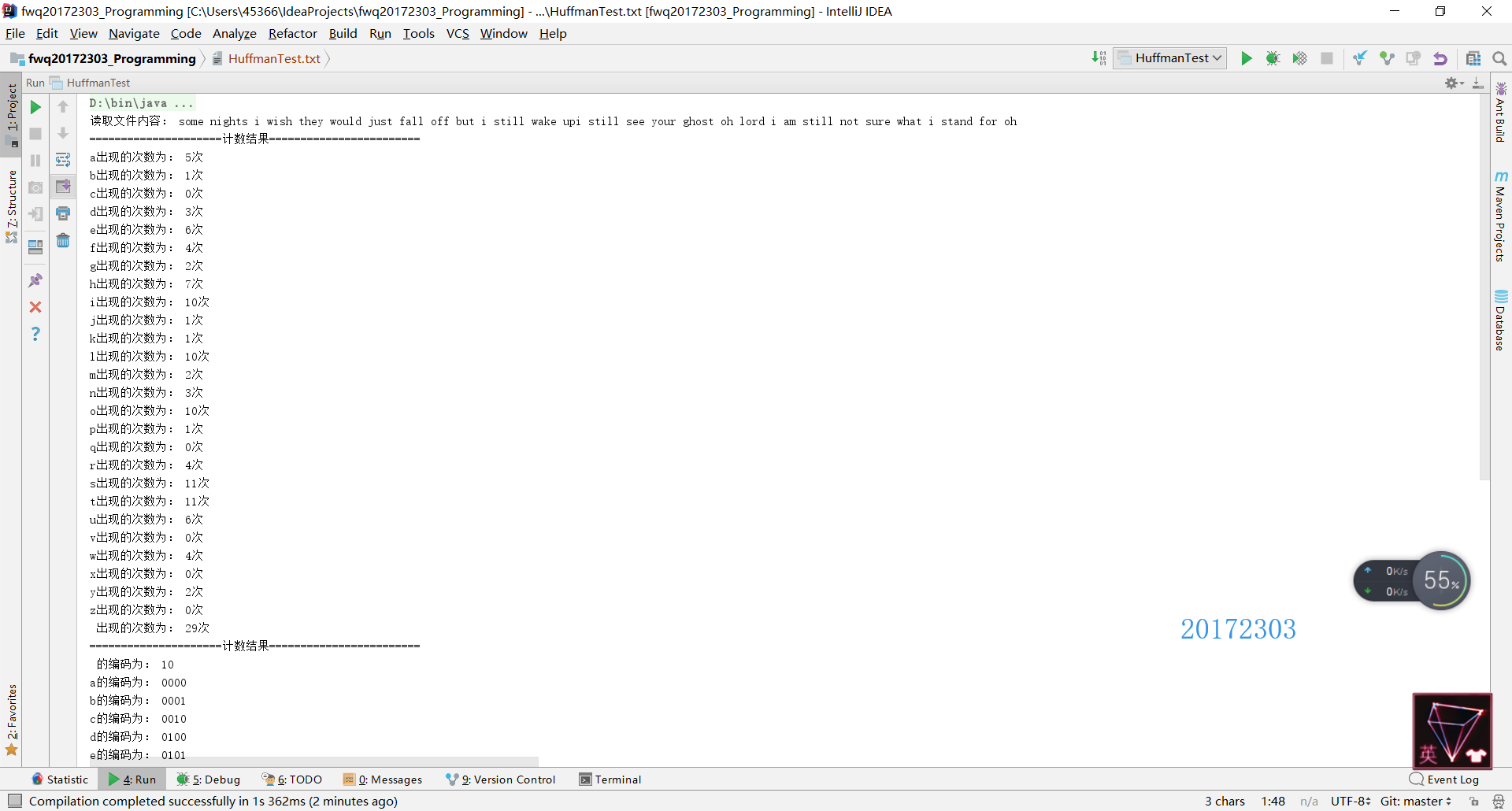
• HuffmanTest类测试结果
  
  
• 编码写入文件
  

参考资料

• 20172303 2017-2018-2 《程序设计与数据结构》第9周学习总结
• 哈夫曼树
• 哈夫曼树的构造