字典树

目录

• 零、前言
• 一、普通Trie树
  • 1.定义？
  • 2.讲解
    • (1).小知识
    • (2).具体实现
  • 3.练习
  • 4.代码
• 二、可持续化Trie树
  • 1.讲解
    • (1).建树 & 插入
    • (2).查询
  • 2.练习
  • 3.代码
• Update

零、前言

这是一篇高开低走的博客

一、普通Trie树

1.定义？

又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

摘自百度百科

2.讲解

又到了喜闻乐见的百度百科自学时间

如果你一头雾水地回来了，那我就成功了，嘿嘿嘿

(1).小知识

它可以用来干嘛？

做题！这不废话

见定义？

而且它的时间复杂度为(O(m|S|))(一般是这样)

(|S|)为字符串长度，(n)个字符串，(m)为操作次数，但其实建树也需要时间(O(n|S|))

字典树开的空间当然就是有多少点就开多少空间(记得加上可能加的点的空间)

(2).具体实现

我们先讲建树

假设我们有(26)个小写字母，组成了长度不超过(50)的单词 (谁家单词这么长) 字符串

比如有：

(aba,aaa,aa,bc)

我们就可以这么建树：

首先我们需要一个超级源点 (原点?)，我比较喜欢用(0)号点(因为不用赋值就是(0))

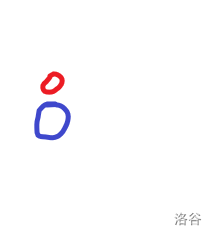
红色数字为点的编号，蓝色圈圈中的黑色字母为当前点的字母，绿色数字为(cnt)，用来记录字符串在哪里结束，有多少个

然后插入第一个字符串(aba)

我们具体的操作为：从源点出发，看一看有没有第一个字母(a)曾经出现过

如果没有，新建一个点作为当前点(源点)的(a)号儿子，然后走到这个儿子上

如果有，直接走到这个儿子上

当我们走到最后一步时，我们需要一个标记表示走到这步的时候就是一个字符串了

所以在每个点中，我们需要一个(cnt)记录字符串出现次数

在我们的这道例题中，当然就有(26)个儿子，一个(cnt)

经过第一个插入操作，我们可以得到这么一棵字典树：

然后我们插入第二个单词：

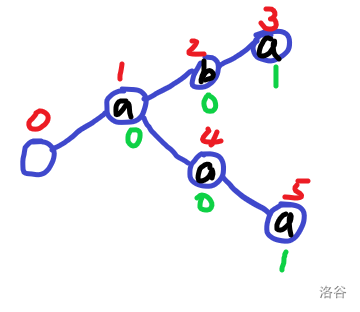
第三个单词：

由于之前已经有(aa)了，所以我们只需走到(aa)，( ext{++}cnt)就好了

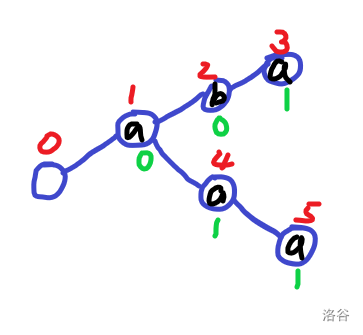
第四个单词，另起一个枝干：

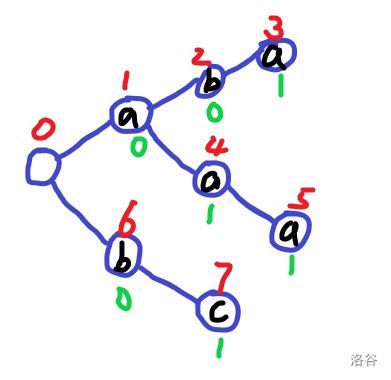
如果你想查询是否存在一个字符串(S)，只需要从源点开始，一步一步走，如果到不了终点或者终点的(cnt)为(0)，就是没有这个字符串

反之则有

最大败笔：图太丑！！！

3.练习

于是他错误的点名开始了(洛谷)

阅读理解(洛谷)

最长异或路径(洛谷)

4.代码

阅读理解代码

//12252024832524
#include <set>
#include <cstdio>
#include <cstring>
using namespace std;

typedef long long LL;
const int MAXN = 25;
int n,num;
char w[MAXN];
struct Tire
{
	int a[26],c;//字母 & 次数 
	set<int> s;
}t[MAXN*10005];//每个单词最大长度 * 单词数 

int Read()
{
	int x = 0,f = 1;char c = getchar();
	while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
	while(c >= '0' && c <= '9'){x = (x<<3) + (x<<1) + (c^48);c = getchar();}
	return x * f;
}
void in(char *w1,int x)//insert
{
	int len = strlen(w1);
	int xb = 0;
	for(int i = 0;i < len;++ i)
	{
		int dz = w1[i] - 'a';
		if(!t[xb].a[dz])
			t[xb].a[dz] = ++num;
		xb = t[xb].a[dz];
		t[xb].c++;
	}
	t[xb].s.insert(x);
}
void Q(char *w1)
{
	int len = strlen(w1);
	int xb = 0;
	for(int i = 0;i < len;++ i)
	{
		int dz = w1[i] - 'a';
		xb = t[xb].a[dz];
		if(t[xb].c == 0)
			return;
	}
	set<int>::iterator it;
	int ans[1005],tot = 0;
	for(it = t[xb].s.begin();it != t[xb].s.end();++ it)
		ans[++tot] = *it;
	for(int i = 1;i < tot;++ i)
		printf("%d ",ans[i]);
	if(tot)
		printf("%d",ans[tot]);
}

int main()
{
	int T = Read();
	for(int wz = 1;wz <= T;++ wz)
	{
		n = Read();
		for(int i = 1;i <= n;++ i)
		{
			scanf("%s",w);
			in(w,wz);
		} 
	}
	int q = Read();
	while(q --)
	{
		scanf("%s",w);
		Q(w);
		if(q)
			putchar('
');
	}
	return 0;
}

最长异或路径代码

//12252024832524
#include <cstdio>
#include <algorithm>
using namespace std; 

typedef long long LL;
const int MAXN = 100005;
const int INF = 2147483647;
int n,tot,ans;
int head[MAXN],xo[MAXN];
struct edge
{
	int v,w,nxt;	
}e[MAXN << 1];
struct trie
{
	int ch[2];
	bool val;
	trie(){ch[0] = ch[1] = 0;}
}t[MAXN * 31];

int Read()
{
	int x = 0,f = 1;char c = getchar();
	while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
	while(c >= '0' && c <= '9'){x = (x*10) + (c^48);c = getchar();}
	return x * f;
}
void Put1(int x)
{
	if(x > 9) Put1(x/10);
	putchar(x%10^48);
}
void Put(int x)
{
	if(x < 0) putchar('-'),x = -x;
	Put1(x);
}
template <typename T>T Max(T x,T y){return x > y ? x : y;}
template <typename T>T Min(T x,T y){return x < y ? x : y;}
template <typename T>T Abs(T x){return x < 0 ? -x : x;}

void Add_Edge(int x,int y,int val)
{
	e[++tot].v = y;
	e[tot].w = val;
	e[tot].nxt = head[x];
	head[x] = tot;
}
void dfs(int x,int fa,int s)
{
	xo[x] = s;
	for(int i = head[x]; i ;i = e[i].nxt)
	{
		if(e[i].v == fa) continue;
		dfs(e[i].v,x,s^e[i].w);
	}
}
void ins(int x)
{
	int now = 0;
	for(int i = 30;i >= 0;-- i)
	{
		bool d = (1<<i)&x;
		if(!t[now].ch[d])
			t[now].ch[d] = ++tot;
		now = t[now].ch[d];
	}
}
void solve(int x)
{
	int now = 0,dz = 0;
	for(int i = 30;i >= 0;-- i)
	{
		bool d = (1<<i)&x;
		if(t[now].ch[d^1])
		{
			now = t[now].ch[d^1];
			dz |= (1 << i);
		}
		else
			now = t[now].ch[d];
	}
	ans = Max(ans,dz);
}

int main()
{
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n = Read();
	for(int i = 1;i < n;++ i)
	{
		int u = Read(),v = Read(),w = Read();
		Add_Edge(u,v,w);
		Add_Edge(v,u,w);
	} 
	dfs(1,0,0);
	tot = 0;
	for(int i = 1;i <= n;++ i)
		ins(xo[i]);
	for(int i = 1;i <= n;++ i)
		solve(xo[i]);
	Put(ans);
	return 0;
}

二、可持续化Trie树

我们可以类比主席树

1.讲解

如果你学懂了普通的(Trie)树，那么我们来学学可持续化的(Trie)树

如果你没有学过主席树，没有关系，虽然学过会更好懂一些

我们拿板题来讲

首先我们需要各个元素(第(i)号元素为(a[i]))的异或前缀和，把(i)的前缀和记为(s[i])

(s[i]oplus s[j](i<j))就可以得到(a[i+1])~(a[j])的异或和(基操，勿6，皆坐，观之)

(1).建树 & 插入

我们的具体思路为，对于每个(s[i])建一棵(Trie)树，当然，这个时候就不是字符串了，而是二进制

尽管时间和空间都无法接受

但是我们发现了一个规律(虽然这并没有什么联系)：

(s[i])与(s[i-1])很明显可以共用很多个节点

对于每个(i)，我们当然需要一个根(rt[i])

然后插入(s[i])的时候我们同时跑(i-1)和(i)

可以省下很多空间，当然也有时间

(2).查询

首先我们把(X oplus s[n])，记为(x)好了，只需要找(x oplus s[i] (l-1le i le r))，使得(x oplus s[i])最大

怎么搞呢，当然就是贪心啦

我们把(x)的二进制表示的第(i)位记为(x_i)

我们贪心的想，如果使得(x_i)变为(1)，一定是最优的，因为如果你(x_i)不为(1)，即为(0)，那么后面的所有位即使都是(1)，加起来也没有(x_i)为(1)大了

所以我们要尽量选$x_i oplus s[j]_i=$1，但是怎么判断是否可以这么选呢？

这时我们的(cnt)就不要为结束的标志了，而是每到一个点就(+1)

我们同时跑(l-1)和(r)，如果(t[r_{now}].cnt - t[(l-1)_{now}].cnt > 0(t)为字典树())，那么就可以选

反之则不行

2.练习

板题(洛谷)

3.代码

板题代码

//12252024832524
#include <cstdio>
#include <algorithm>
using namespace std; 

typedef long long LL;
const int MAXN = 300005;
const int MAXLOG = 23;
int n,m;
int a[MAXN * 2],rt[MAXN * 2];
char opt[2];

int Read()
{
	int x = 0,f = 1;char c = getchar();
	while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
	while(c >= '0' && c <= '9'){x = (x*10) + (c^48);c = getchar();}
	return x * f;
}
void Put1(int x)
{
	if(x > 9) Put1(x/10);
	putchar(x%10^48);
}
void Put(int x,char c = -1)
{
	if(x < 0) putchar('-'),x = -x;
	Put1(x);
	if(c >= 0) putchar(c);
}
template <typename T>T Max(T x,T y){return x > y ? x : y;}
template <typename T>T Min(T x,T y){return x < y ? x : y;}
template <typename T>T Abs(T x){return x < 0 ? -x : x;}

int tot;
struct trie
{
	int ch[2],cnt;
}t[MAXN * MAXLOG * 2];
void ins(int &x1,int x2,int d,int val)
{
	x1 = ++tot;
	t[x1] = t[x2];
	t[x1].cnt ++;
	if(d == -1) return;
	bool now = val & (1 << d);
	ins(t[x1].ch[now],t[x2].ch[now],d-1,val);
}
int trieq(int x1,int x2,int d,int val)
{
	if(d == -1 || (!x1 && !x2)) return 0;
	bool now = val & (1 << d);
	if(t[t[x1].ch[!now]].cnt > t[t[x2].ch[!now]].cnt)
		return (1 << d) + trieq(t[x1].ch[!now],t[x2].ch[!now],d-1,val);
	else return trieq(t[x1].ch[now],t[x2].ch[now],d-1,val);
}

int main()
{
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n = Read()+1;
	m = Read();
	for(int i = 2;i <= n;++ i) a[i] = Read() ^ a[i-1];
	for(int i = 1;i <= n;++ i) ins(rt[i],rt[i-1],MAXLOG,a[i]);
	while(m --)
	{
		scanf("%s",opt);
		if(opt[0] == 'A') n++,a[n] = Read() ^ a[n-1],ins(rt[n],rt[n-1],MAXLOG,a[n]);
		else 
		{
			int l = Read(),r = Read();
			Put(trieq(rt[r],rt[l-1],MAXLOG,Read()^a[n]),'
');
		}
	}
	return 0;
}

Update

(2020.05.18)，更新了以前没学懂的时候用的指针模板(现已改为非指针)