前言
回滚莫队入门题
考场状态:人手一份莫队,但我就是(TLE)
(QAQ)
题目
前置知识
普通莫队
讲解
由于普通的莫队又要加,又要减,不好处理变小的最大值,处理的话就要带(log),然后就(TLE)了
所以要高级的:回滚莫队
望文生义:往回滚的莫队
首先分块,把询问区间先按左端点的块排序,相同按右端点从小到大排序
这样排序是为了方便我们就下来的操作
接下来依次处理排序后的询问
把莫队的(l,r)放到当前询问所属块的右端点,假设红色部分是询问区间:
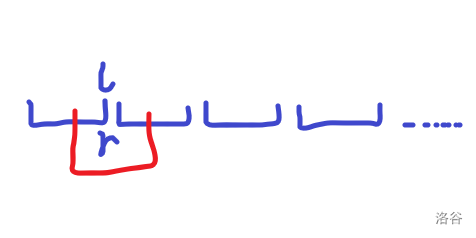
这样我们就只用扩张,最大值当然也很好求
到了第二个询问(绿色):
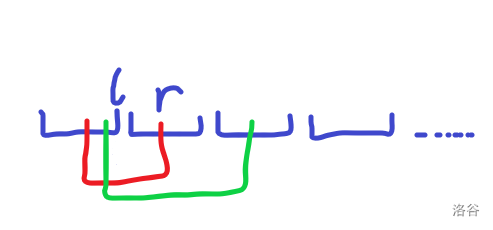
尽管(l)不知道在哪里,但它一定在这个块里面,所以我们直接退滚回右端点,但(r)由于我们是从小到大排序的,不需要回退
而上图的(l)到(r)的最大值我们是可以提前记录的
直接接着走就行了:
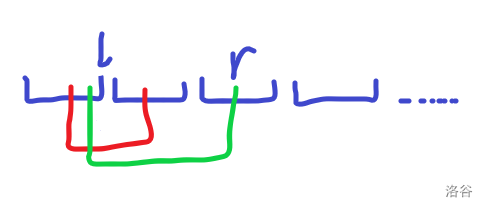
对于每次操作,(l)回到原点,(r)接着走就行了
如果我们当前这个询问的块是上一个询问的下一个块
即我们跨过了一个块
直接清空莫队用来计数的数组(()我的(tot)数组())
重新再来,重复上面的操作,只是块变成了下一个而已
就相当于我们对于每一个块做一次莫队(我的理解,但愿你不要。。。)
但这么打出来并不能过,要( ext{WA})
我们考虑到还有这种情况:

( ext{woc}),(r)还要往左边走可咋整?
想想你的莫队会怎么走?
直接走啊!
先走(r),把计数的数组先减,并不用更新答案
然后再走(l),一定会把减成负数的计数的数组加回来(看图),这个时候再更新答案就可以了
时间复杂度(O(nsqrt{n}))
代码
//12252024832524
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 100005;
int n,Q;
LL lsh[MAXN],lshtot;
int tot[MAXN];
int belong[MAXN];
LL ans[MAXN];
struct query
{
int l,r,ID;
bool operator < (const query &px) const{
if(belong[l] != belong[px.l])
return belong[l] < belong[px.l];
return r < px.r;
}
}q[MAXN];
struct node
{
int x,ID;
}p[MAXN];
int Read()
{
int x = 0,f = 1;char c = getchar();
while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9'){x = (x*10) + (c^48);c = getchar();}
return x * f;
}
void Put1(LL x)
{
if(x > 9) Put1(x/10);
putchar(x%10^48);
}
void Put(LL x)
{
if(x < 0) putchar('-'),x = -x;
Put1(x);
}
template <typename T>T Max(T x,T y){return x > y ? x : y;}
template <typename T>T Min(T x,T y){return x < y ? x : y;}
template <typename T>T Abs(T x){return x < 0 ? -x : x;}
bool cmp1(node x,node y)
{
return x.x < y.x;
}
bool cmp2(node x,node y)
{
return x.ID < y.ID;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = Read();
Q = Read();
int sq = sqrt(n);
for(int i = 1;i <= n;++ i)
{
p[i].x = Read();
p[i].ID = i;
belong[i] = (i-1) / sq + 1;
}
sort(p+1,p+n+1,cmp1);
for(int i = 1;i <= n;++ i)
{
if(p[i].x != lsh[lshtot])
lsh[++lshtot] = p[i].x;
p[i].x = lshtot;
}
sort(p+1,p+n+1,cmp2);
for(int i = 1;i <= Q;++ i)
{
q[i].l = Read();
q[i].r = Read();
q[i].ID = i;
}
sort(q+1,q+Q+1);
int l,r = 0;
LL now = 0,lst = 0;
for(int i = 1;i <= Q;++ i)
{
l = sq * belong[q[i].l];//该块右端点
if(belong[q[i].l] > belong[q[i-1].l])
{
for(int j = 1;j <= lshtot;++ j)
tot[j] = 0;
r = l - 1;
lst = now = 0;
}
now = lst;
while(r < q[i].r)
{
r++;
tot[p[r].x]++;
now = Max(now,tot[p[r].x] * lsh[p[r].x]);
}
while(r > q[i].r)
{
tot[p[r].x]--;
r--;
}
lst = now;
while(l > q[i].l)
{
l--;
tot[p[l].x]++;
now = Max(now,tot[p[l].x] * lsh[p[l].x]);
}
ans[q[i].ID] = now;
for(int j = sq * belong[q[i].l]-1;j >= l;-- j)
tot[p[j].x]--;
}
for(int i = 1;i <= Q;++ i)
{
Put(ans[i]);
putchar('
');
}
return 0;
}