给定一个未填好的(9*9)的数独,输出完整的数独.
数独最最最基础的是要掌握行,列和一个九宫格的表示方法,其它的其实就和八皇后问题的思想差不多了.
行和列很容易,重点就是一个小九宫格(如何由行,列得到处于第几个九宫格?)了,直接给出:
ge[(i-1)/3*3+(j-1)/3+1][a[i][j]]=1
((i-1)/3*3+(j-1)/3+1)如果不能理解为什么是这个式子,就记住吧(一般数独题都要用得到),但手动模拟几下,其实还是很好理解的.
int a[10][10],hang[10][10],lie[10][10],ge[10][10];
void print(){//输出完整的九宫格
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++)
printf("%d ",a[i][j]);
printf("
");
}
exit(0);//这里不能用return 0,就用这个吧.
}
void dfs(int x,int y){
if(a[x][y]){
if(x==9&&y==9)print();
if(y==9)dfs(x+1,1);
else dfs(x,y+1);
}
//如果[x,y]位置上已经有值了,则分类讨论如何走下去
//这个else一定要加
else for(int i=1;i<=9;i++){
if(!hang[x][i]&&!lie[y][i]&&!ge[(x-1)/3*3+(y-1)/3+1][i]){
a[x][y]=i;
hang[x][i]=1;
lie[y][i]=1;
ge[(x-1)/3*3+(y-1)/3+1][i]=1;
//标记
if(x==9&&y==9)print();
if(y==9)dfs(x+1,1);
else dfs(x,y+1);
//同上,走完一步后,分类讨论如何继续下去
a[x][y]=0;
hang[x][i]=0;
lie[y][i]=0;
ge[(x-1)/3*3+(y-1)/3+1][i]=0;
//回溯
}
}
}
int main(){
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++){
a[i][j]=read();
if(a[i][j]){
hang[i][a[i][j]]=1;
lie[j][a[i][j]]=1;
ge[(i-1)/3*3+(j-1)/3+1][a[i][j]]=1;
}
//如果[i,j]位置上是x,则第i行,第j列
//和[i,j]所在的小九宫格都不能放x了,这里做个标记
}
dfs(1,1);//从[1,1]开始搜索
return 0;
}
数独升级了!!!本题中,数独与靶结合,(9*9)的正方形中不同区域还有不同的权值,如图所示:
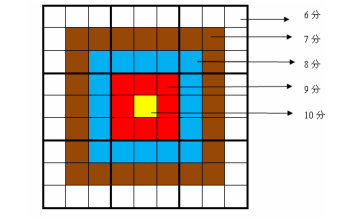
我们现在要求如何填数独,能够使得获得的总分最大.每一个小格子的获得分数是该格子的权值与该格子上填的数的乘积.
注意:当数独无解时,输出-1;
我们在搜索时大可不必管什么最大得分,就每次搜索完之后比较一下大小就行了.但因为题目这样出,显然就是会有很多个成立的填数独的方法,所以我们现在最大的问题是,如何不超时!!!那么搜索就要考虑如何剪枝了.
剪枝:不用解释也能明白吧,从可能情况最少的那行开始填,能够大大减少搜索状态.
但别看这个剪枝原理很简单,为了它,搜索前期得做很多工作.
int num,now,ans=-1;//ans赋初值-1,就懒得特判了
int a[10][10],dfs[101][5];
int hang[10][10],lie[10][10],ge[10][10];
struct sodu{
int sum,line;
}b[10];
//sum和line记录的就是每一行各自没有填的格子的数量
bool cmp(sodu x,sodu y){return x.sum<y.sum;}
//按照没有填的格子的数量从小到大排序
int point(int x,int y){
if(x==1||y==1||x==9||y==9)return 6;
if(x==2||y==2||x==8||y==8)return 7;
if(x==3||y==3||x==7||y==7)return 8;
if(x==4||y==4||x==6||y==6)return 9;
return 10;
}
//通过一个函数解决每个格子的带权值问题
void DFS(int x,int val){
if(x>num){
ans=max(ans,val);
return;
}
//数独填完了,就比较一下大小.
for(int i=1;i<=9;i++){
if(!hang[dfs[x][0]][i]&&!lie[dfs[x][1]][i]&&!ge[dfs[x][2]][i]){
hang[dfs[x][0]][i]=1;
lie[dfs[x][1]][i]=1;
ge[dfs[x][2]][i]=1;
DFS(x+1,val+dfs[x][3]*i);
hang[dfs[x][0]][i]=0;
lie[dfs[x][1]][i]=0;
ge[dfs[x][2]][i]=0;
}
}
}
int main(){
for(int i=1;i<=9;i++)
b[i].line=i;
//结构体排序的时候行号不跑丢
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++){
a[i][j]=read();
if(a[i][j]){
hang[i][a[i][j]]=1;
lie[j][a[i][j]]=1;
ge[(i-1)/3*3+(j-1)/3+1][a[i][j]]=1;
now+=point(i,j)*a[i][j];
}
//如果[i,j]上直接有初值,除了记录行,列,格的情况
//把已经获得的分数也累积进now
else b[i].sum++;
//如果[i,j]上没有初值,则第i行上没填的格子的数量加1
}
sort(b+1,b+9+1,cmp);
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++){
if(a[b[i].line][j]==0){
dfs[num][0]=b[i].line;
dfs[num][1]=j;
dfs[num][2]=(b[i].line-1)/3*3+(j-1)/3+1;
dfs[num][3]=point(b[i].line,j);
num++;
}
}
//num直接记录的是整个9*9上没填数的格子的数量
//dfs数组第一维其实就是搜索顺序
//即dfs[0][]就是我们第一个开始搜索填数的对象
//根据上面的结构体排序,它位于未填格子数最少的一行
//dfs[][0]:行;[1]:列;[2]:格;[3]:权值
DFS(0,now);
printf("%d
",ans);
return 0;
}