<更新提示>
<第一次更新>
<正文>
标题统计
题目描述
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符? 注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字 符数时,空格和换行符不计算在内。
输入格式
输入文件只有一行,一个字符串 s。
输出格式
输出文件只有一行,包含一个整数,即作文标题的字符数(不含空格和换行符)。
样例数据
input1
234
output1
3
input2
Ca 45
output2
4
样例说明
样例 1 :标题中共有 3 个字符,这 3 个字符都是数字字符。
样例 2 :标题中共有 5 个字符,包括 1 个大写英文字母, 1 个小写英文字母和 2 个数字字符, 还有 1 个空格。由于空格不计入结果中,故标题的有效字符数为 4 个。
数据规模与约定
规定∣s∣ 表示字符串 s 的长度(即字符串中的字符和空格数)。
对于 %40 的数据,1 ≤ |s| ≤ 5,保证输入为数字字符及行末换行符。
对于 %80 的数据,1 ≤ |s| ≤ 5,输入只可能包含大、小写英文字母、数字字符及行末换行符。
对于 %100 的数据,1 ≤ |s| ≤ 5,输入可能包含大、小写英文字母、数字字符、空格和行末换行符。
时间限制:1s
空间限制:256MB
解析
T1和往年一样,还是签到题。不过这一次好像更注重考察语言了,不少不熟悉语言的小伙伴可能就没有分了啦。
大概是考察如何处理输入吧,会用(getline())的基本都用了(getline())了吧,当然,不会用的还有其他的办法,主要是(while(cin>>str))和(scanf())读到换行符为止。这样的话,只要暴力统计一下就可以了啦。
(Code:)
#include<bits/stdc++.h>
using namespace std;
string s;int ans=0;
int main(void)
{
freopen("title.in","r",stdin);
freopen("title.out","w",stdout);
getline(cin,s);
for(int i=0;i<s.size();i++)
{
if(s[i]!=' ')ans++;
}
printf("%d
",ans);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
char s;
int ans=0;
int main()
{
freopen("title.in","r",stdin);
freopen("title.out","w",stdout);
while (cin>>s)
{
if(s>='0'&&s<='9'||s>='a'&&s<='z'||s>='A'&&s<='Z')ans++;
}
cout<<ans<<endl;
return 0;
}
龙虎斗
题目描述
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏,游戏的棋盘是一条线段,线段上有 n个兵营(自左至右编号 1 ∼n),相邻编号的兵营之间相隔 1 厘米,即棋盘为长度为 n-1 厘米的线段。i 号兵营里有 ci位工兵。
下面图 1 为 n=6的示例:

轩轩在左侧,代表“龙”;凯凯在右侧,代表“虎”。 他们以 m 号兵营作为分界, 靠左的工兵属于龙势力,靠右的工兵属于虎势力,而第 m号兵营中的工兵很纠结,他们不属于任何一方。
一个兵营的气势为:该兵营中的工兵数 × 该兵营到 m 号兵营的距离;参与游戏 一方的势力定义为:属于这一方所有兵营的气势之和。
下面图 2 为 n = 6,m = 4 的示例,其中红色为龙方,黄色为虎方:

游戏过程中,某一刻天降神兵,共有 s1位工兵突然出现在了 p1号兵营。作为轩轩和凯凯的朋友,你知道如果龙虎双方气势差距太悬殊,轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续,你需要选择一个兵营 p2,并将你手里的 s2位工兵全部派往 兵营 p2,使得双方气势差距尽可能小。
注意:你手中的工兵落在哪个兵营,就和该兵营中其他工兵有相同的势力归属(如果落在 m 号兵营,则不属于任何势力)。
输入格式
输入文件的第一行包含一个正整数n,代表兵营的数量。
接下来的一行包含 n 个正整数,相邻两数之间以一个空格分隔,第 i个正整数代 表编号为 i 的兵营中起始时的工兵数量 ci。
接下来的一行包含四个正整数,相邻两数间以一个空格分隔,分别代表 m,p1,s1,s2。
输出格式
输出文件有一行,包含一个正整数,即 p2,表示你选择的兵营编号。如果存在多个编号同时满足最优,取最小的编号。
样例数据
input1
6
2 3 2 3 2 3
4 6 5 2
output1
2
input2
6
1 1 1 1 1 16
5 4 1 1
output2
1
样例说明
样例1:见问题描述中的图 2。
双方以 m=4号兵营分界,有 s1=5位工兵突然出现在p1=6号兵营。 龙方的气势为:
2×(4−1)+3×(4−2)+2×(4−3)=14
虎方的气势为:
2×(5−4)+(3+5)×(6−4)=18
当你将手中的 s2=2s2=2位工兵派往 p2=2号兵营时,龙方的气势变为:
14+2×(4−2)=18
此时双方气势相等。
样例2:
双方以 m = 5号兵营分界,有 s1=1位工兵突然出现在 p1=4号兵营。
龙方的气势为:
1×(5−1)+1×(5−2)+1×(5−3)+(1+1)×(5−4)=11
虎方的气势为:
16×(6−5)=16
当你将手中的 s2=1位工兵派往 p2=1号兵营时,龙方的气势变为:
11+1×(5−1)=15
此时可以使双方气势的差距最小。
数据规模与约定
1<m<n,1≤p1≤n。
对于%20 的数据,(n=3,m=2,ci=1,s1,s2≤100。)
另有%20 的数据,(n≤10,p1=m,ci=1,s1,s2≤100。)
对于%60 的数据,(n≤100,ci=1,s1,s2≤100。)
对于%80 的数据,(n≤100,ci,s1,s2≤100。)
对于%100 的数据,(n≤10^5,ci,s1,s2≤10^9。)
时间限制:1s
空间限制:256MB
解析
今年的第二题没有往年怎么简单啦。这回T2虽然说也没有考算法,但是细节问题就很多了,于是就有了不少坑点:
1.爆int
2.min的初值需要赋到MAX_LONGLONG大小
3.需要注意把工兵放在m号兵营的情况
那么大体思路是这样的,我们暴力枚举把(s2)个工兵放在每一个兵营的情况,看看放在哪里呢得到最优解,直接输出即可。那么,这里就有一个显而易见的优化了:那一边初始的气势值总和最小,那就在那一边枚举。但是,这就如3.,无论是那一边,我们都要判断是否把(s2)个工兵放在(m)号兵营会取得更优的答案,因为存在如下一种情况:
一开始双方势力值总和的差较小,我们在势力值总和较小的一边枚举,但是(s2)的值巨大,无论放在哪里,新势力值的差比原势力值的差还大,此时,不如把工兵放在(m)号兵营处,让势力值总和不变化
如果这些都注意到了,那么这题就解决了。
(Code:)
#include<bits/stdc++.h>
using namespace std;
inline void read(long long &k)
{
long long x=0,w=0;char ch;
while(!isdigit(ch))w|=ch=='-',ch=getchar();
while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
k=(w?-x:x);return;
}
const int Maxn=100000+80;
long long n,c[Maxn],m,p1,s1,s2,vleft=0,vright=0,Mindif=0x3f3f3f3f,ans;
inline void input(void)
{
read(n);
for(int i=1;i<=n;i++)read(c[i]);
read(m),read(p1);
read(s1),read(s2);
c[p1]+=s1;
}
inline void init(void)
{
for(int i=1;i<m;i++)vleft+=(c[i]*(m-i));
for(int i=m+1;i<=n;i++)vright+=(c[i]*(i-m));
}
inline void work(void)
{
if(vleft<vright)
{
for(int i=1;i<=m;i++)
{
long long l=vleft+s2*(m-i);
long long dif=abs(vright-l);
if(dif<Mindif)
{
Mindif=dif;
ans=i;
}
}
}
else if(vright<vleft)
{
for(int i=m;i<=n;i++)
{
long long r=vright+(i-m)*s2;
long long dif=abs(r-vleft);
if(dif<Mindif){
Mindif=dif;
ans=i;
}
}
}
else
{
ans=m;
}
}
int main(void)
{
freopen("fight.in","r",stdin);
freopen("fight.out","w",stdout);
input();
init();
work();
printf("%lld
",ans);
return 0;
}
摆渡车
题目描述
有 n 名同学要乘坐摆渡车从人大附中前往人民大学,第 i 位同学在第 ti分钟去 等车。只有一辆摆渡车在工作,但摆渡车容量可以视为无限大。摆渡车从人大附中出发、 把车上的同学送到人民大学、再回到人大附中(去接其他同学),这样往返一趟总共花费m分钟(同学上下车时间忽略不计)。摆渡车要将所有同学都送到人民大学。
凯凯很好奇,如果他能任意安排摆渡车出发的时间,那么这些同学的等车时间之和最小为多少呢?
注意:摆渡车回到人大附中后可以即刻出发。
输入格式
第一行包含两个正整数 n,m,以一个空格分开,分别代表等车人数和摆渡车往返 一趟的时间。
第二行包含 n 个正整数,相邻两数之间以一个空格分隔,第 i 个非负整数 ti代 表第 i 个同学到达车站的时刻。
输出格式
输出一行,一个整数,表示所有同学等车时间之和的最小值(单位:分钟)。
样例数据
input1
5 1
3 4 4 3 5
output1
0
input2
5 5
11 13 1 5 5
output2
4
样例说明
样例1:
同学 1 和同学 4 在第 3 分钟开始等车,等待 0 分钟,在第 3 分钟乘坐摆渡车出发。摆渡车在第 4分钟回到人大附中。
同学 2 和同学 3 在第 4 分钟开始等车,等待 0 分钟,在第 4 分钟乘坐摆渡车 出发。摆渡车在第 5 分钟回到人大附中。
同学 5 在第 5 分钟开始等车,等待 0 分钟,在第 5 分钟乘坐摆渡车出发。自此 所有同学都被送到人民大学。总等待时间为 0。
样例2:
同学 3 在第 1 分钟开始等车,等待 0 分钟,在第 1 分钟乘坐摆渡车出发。摆渡 车在第 6分钟回到人大附中。
同学 4 和同学 5 在第 5 分钟开始等车,等待 1 分钟,在第 6 分钟乘坐摆渡车 出发。摆渡车在第 11 分钟回到人大附中。
同学 1 在第 11 分钟开始等车,等待 2 分钟;同学 2 在第 13 分钟开始等车, 等待 0 分钟。他/她们在第 13 分钟乘坐摆渡车出发。自此所有同学都被送到人民大学。 总等待时间为 4。
可以证明,没有总等待时间小于 4 的方案。
数据规模与约定
对于%10 的数据,(n≤10,m=1,0≤ti≤100。)
对于%30 的数据,(n≤20,m≤2,0≤ti≤100。)
对于%50 的数据,(n≤500,m≤100,0≤ti≤10^4。)
另有%20 的数据,(n≤500,m≤10,0≤ti≤4×10^6。)
对于%100 的数据,(n≤500,m≤100,0≤ti≤4×10^6。)
时间限制:2s
空间限制:256MB
解析
这就是今年的毒瘤T3了,可以说是近几年来最难的一道题,比今年T4还难。
可是这道题的题面竟然异常简洁,让人一看就懂。有没有人像我一样一看就觉得简单的(`・ω・´),然后就死在这了。
首先按时间排序,这是一定的。最容易让人想到的就是(O(n^3))的(dp)了,设(f[i])代表前(i)个同学到达的最小等待时间总和,那么暴力转移是不会超时的。但是考场上怎么都不会想到的是,这样的dp在转移时的花费是会计算错误的,而且小数据基本调不出来,主要原因是:我们不知道在转移第(i)位同学时车是什么时候到的,也就是不知道转移的出发时间。所以在大数据上,一维的(dp)就基本全错了。
但是这个错误算法也给我们一个启示,我们就可以借此来改进dp了。设(f[i][j])代表前i个同学,第(i)个同学在第(t[i]+j)分钟到达的最小等待时间总和,这样的状态就不会出错。其实,这样设置后我们可以很简单地划分阶段,(f[i][j])不需要从(f[k][l])转移,只需要从(f[i-1][k])转移即可,因为(i)个同学必然属于以下两类中的一类:
1.第(i)个同学和第(i-1)个同学坐同一辆车
2.第(i)个同学和第(i-1)个同学不坐同一辆车
那么我们来讨论转移的细节。
先看一个最基本的问题,两位到达时间差超过(m)且到达时间相邻的同学必然不坐同一辆车,因为他们的时间间隔足以让车往返一趟。
那么状态第二维的上限只需要开到(2m)大小即可,达到上限的情况就是和他同时来的一个同学直接坐车走了,花费m分钟,车回来后再送他,又花费m分钟,在第(t[i]+2m)分钟时,前i位同学全部到达。
此时,我们利用阶段转移:
那么三重循环就解决了呀。
(Code:)
#include<bits/stdc++.h>
using namespace std;
const int N=580,M=580,T=4*1e6+80,INF=0x3f3f3f3f;
int n,m,t[N]={},f[N][2*M]={},ans=INF;
inline void input(void)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&t[i]);
}
inline void init(void)
{
sort(t+1,t+n+1);
for(int i=1;i<=m*2;i++)f[1][i]=i;
}
inline void solve(void)
{
for(int i=2;i<=n;i++)
{
for(int j=0;j<2*m;j++)
{
f[i][j]=INF;
for(int k=0;k<2*m;k++)
{
if(t[i-1]+k==t[i]+j||t[i-1]+k+m<=t[i]+j)f[i][j]=min(f[i][j],f[i-1][k]+j);
}
if(i==n)ans=min(ans,f[i][j]);
}
}
}
int main(void)
{
freopen("bus.in","r",stdin);
freopen("bus.out","w",stdout);
input();
init();
solve();
printf("%d
",ans);
return 0;
}
对称二叉树
题目描述
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
1.二叉树;
2.将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 id 表示节点编号。
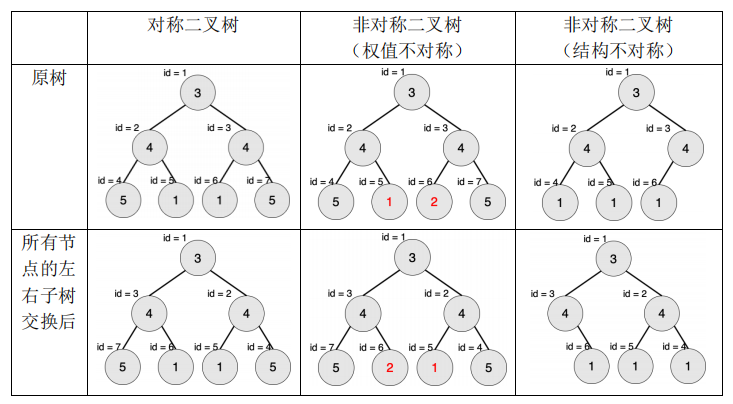
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 T 为子树根的一棵“子 树”指的是:节点T 和它的全部后代节点构成的二叉树。
输入格式
第一行一个正整数 n,表示给定的树的节点的数目,规定节点编号1∼n,其中节点 1 是树根。
第二行 n 个正整数,用一个空格分隔,第 i 个正整数vi代表节点 i的权值。
接下来 n 行,每行两个正整数 li,ri,分别表示节点 i的左右孩子的编号。如果不存在左 / 右孩子,则以 -1表示。两个数之间用一个空格隔开。
输出格式
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
样例数据
input1
2
1 3
2 -1
-1 -1
output1
1
input2
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
output2
3
样例说明
样例1:
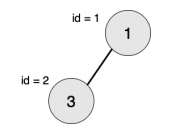
最大的对称二叉子树为以节点 2 为树根的子树,节点数为 1。
样例2:
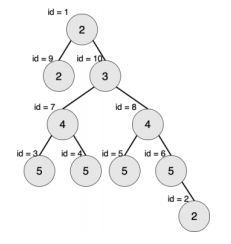
最大的对称二叉子树为以节点 7 为树根的子树,节点数为 3。
数据规模与约定
共 25 个测试点。
(v_i≤1000。)
测试点 (1∼3,n≤10),保证根结点的左子树的所有节点都没有右孩子,根结点的右 子树的所有节点都没有左孩子。
测试点 (4∼8,n≤10)。
测试点 (9∼12,n≤10^5),保证输入是一棵“满二叉树” 。
测试点 (13∼16,n≤10^5),保证输入是一棵“完全二叉树”。
测试点 (17∼20,n≤10^5),保证输入的树的点权均为 1。
测试点 (21∼25,n≤10^6)。
时间限制:1s
空间限制:256MB
本题约定
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 1。
树的深度:树中节点的最大层次称为树的深度。
满二叉树:设二叉树的深度为 h,且二叉树有 2h-1个节点,这就是满二叉树。
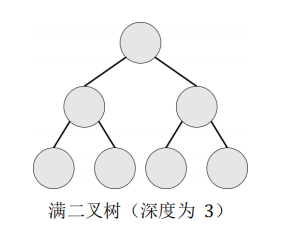
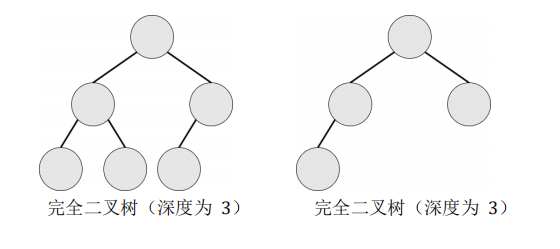
完全二叉树:设二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大 个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
解析
这大概就是和T3放反了的T4吧。一看题面,大部分同学都被吓住了吧,一堆树转来转去的,大概又是什么高级算法。
实际上,这还真就不是了...
总的思路,就是暴力。先暴力枚举每一个点作为根节点,然后判断以该节点作为根的子树是否符合要求,然后就可以更新答案了。
重点在于怎么判断呢?用样例推一下,可以发现规律:
以一个深度为三的二叉树为例,如果符合要求,根节点的左右儿子相等,且满足:
1.左儿子的左儿子 等于 右儿子的右儿子
2.左儿子的右儿子 等于 右儿子的左儿子
3.如果需要比较的两个节点均为空,视为他们相等
那么我们称该根节点的左右儿子为一个符合(Check)要求的点对((u,v)),也就是说点对((u,v))符合要求,他满足:
1.(u=v)
2.(leftson_u=rightson_v)
3.(rightson_u=leftson_v)
4.如果需要比较的两个节点均为空,视为他们相等
再以深度为四的二叉树为例,如果符合要求,他的左右儿子需满足(Check)的要求,且:左儿子的左儿子 和 右儿子的右儿子满足(Check),左儿子的右儿子 和 右儿子的左儿子满足(Check)。
发现三层的二叉树的规律很简单,但如果你发现(Check)这个规则是递归适用的,那么这道题就做出来了,这个就是判断的规则。
如果以一个节点为根它满足对称二叉树的要求,那么用以他为根的子树大小更新答案即可,子树大小用dfs暴力预处理。
分类讨论满二叉树和链的情况,时间复杂度是(O(nlog_2n)),足以完成本题。
当然还有更高级的算法,例如中序遍历求最长回文子串,树哈希等,这里不再提及。
(Code:)
#include<bits/stdc++.h>
using namespace std;
inline void read(int &k)
{
int x=0,w=0;char ch;
while(!isdigit(ch))w|=ch=='-',ch=getchar();
while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
k=(w?-x:x);return;
}
int n,val[1000080],son[1000080][2],size[1000080],ans=0;
inline void input(void)
{
read(n);
for(int i=1;i<=n;i++)read(val[i]);
for(int i=1;i<=n;i++)
{
read(son[i][0]);
read(son[i][1]);
}
}
inline void get_size(int root)
{
size[root]=1;
if(son[root][0]!=-1)
{
get_size(son[root][0]);
size[root]+=size[son[root][0]];
}
if(son[root][1]!=-1)
{
get_size(son[root][1]);
size[root]+=size[son[root][1]];
}
}
inline bool check(int x,int y)
{
if(x==-1&&y==-1)return true;
if(x!=-1&&y!=-1&&val[x]==val[y]&&check(son[x][0],son[y][1])&&check(son[x][1],son[y][0]))return true;
return false;
}
int main(void)
{
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
input();
get_size(1);
for(int i=1;i<=n;i++)
{
int x=son[i][0],y=son[i][1];
if(check(x,y))
{
ans=max(ans,size[i]);
}
}
printf("%d
",ans);
return 0;
}
<后记>
这一次NOIP没考好,主要是时间安排不对,在T3上花的时间太多了,确实也值得反思。多参加模拟赛,训练应考能力和心态吧。