sss

<更新提示>

<第一次更新> 更新了基础部分
<第二次更新>更新了(lazytag)标记的讲解

---

<正文>

线段树 Segment Tree

今天来讲一下经典的线段树。

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

简单的说，线段树是一种基于分治思想的数据结构，用来维护序列的区间特殊值，相对于树状数组，线段树可以做到更加通用，解决更多的区间问题。

性质

• 1.线段树的每一个节点都代表了一个区间
• 2.线段树是一棵二叉树，具有唯一的根节点，其中，根节点代表的是整个区间([1,n])
• 3.线段树的每一个叶节点代表的是长度为(1)的元区间([x,x])
• 4.对于每一个节点([l,r])，它的左儿子被定义为([l,mid])，右儿子被定义为([mid+1,r])

如图，这就是一棵维护了区间([1,10])的线段树。

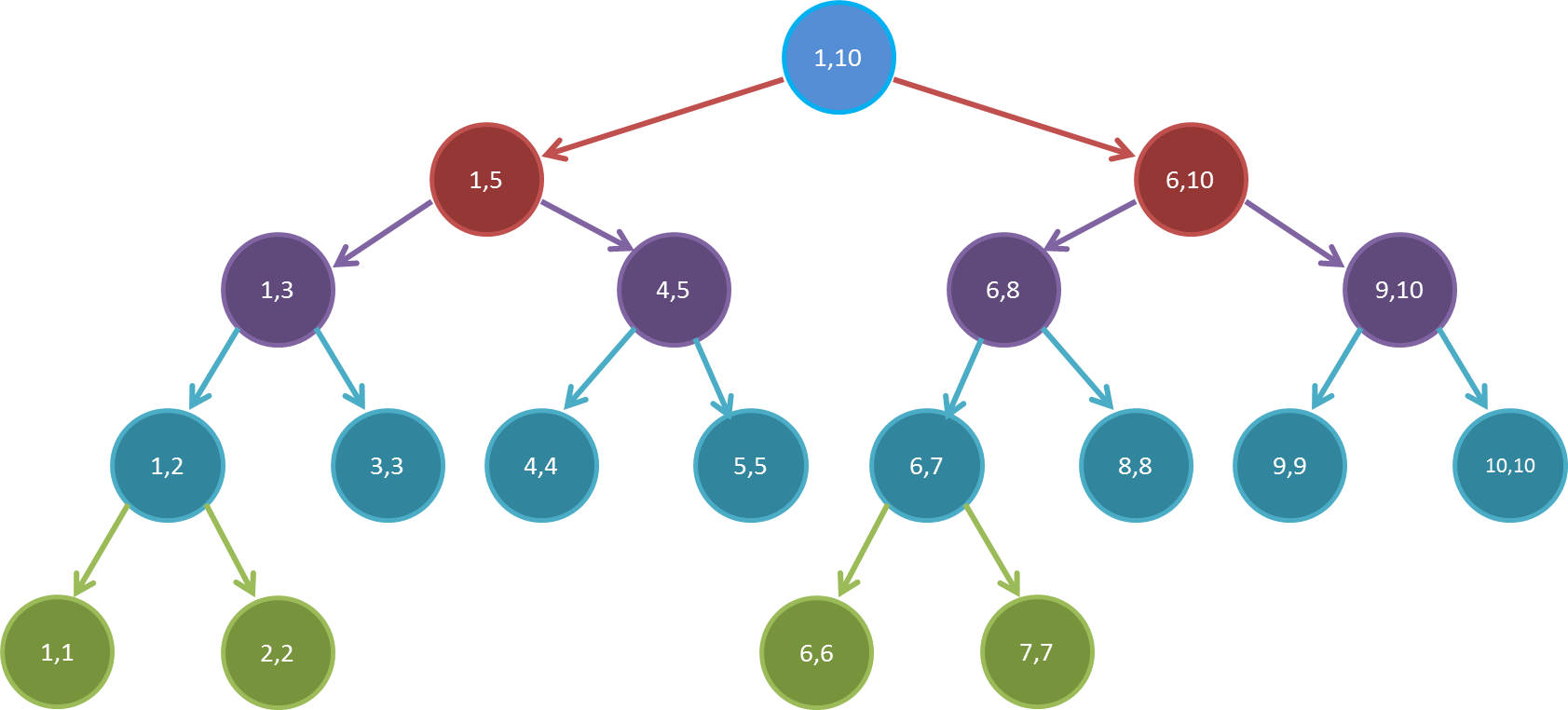
我们还可以发现，线段树层数为(log_2n)层，除去最后一层，线段树是一棵完全二叉树。

建树 (build)

我们来考虑一下如何储存并建立一棵线段树。

由于线段树是二叉树，所以我们可以直接用数组存储结点的编号，即对于节点(x)储存在(a[p])处，我们令(x)的左儿子储存在(a[p*2])处，右儿子储存在(a[p*2+1])处，这样就可以快速地找到节点之间的父子关系。

理想状态下，(n)个叶节点的满二叉树有((sum_{i=0}^{2^i=n}2^i)=2n-1)个节点，但由于最后一层至多还可能有(2n)个节点，所以数组空间要开到(4n)大小。

我们先来看一个维护区间最大值的例子。

对于线段树的每一个节点，我们可以额外的设置一个变量(Max)代表该节点所代表区间中的最大值，显然有:(Max(p)=max(Max(p*2),Max(p*2+1)))，那么我们可以用如下方法建树。

(Code:)

struct SegmentTree
{
	int p,l,r,Max;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define p(x) tree[x].p
	#define Max(x) tree[x].Max
}tree[N*4];
inline void build(int p,int l,int r)//对于节点p，代表的区间为[l,r]
{
	l(p)=l,r(p)=r;//左右边界赋值
	if(l==r){Max(p)=0;return;}//如果为叶节点，直接赋值为权值
	int mid=(l+r)/2;
	//递归构建子树
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	Max(p)=max(Max(p*2),Max(p*2+1));//回溯更新最大值
}

修改 (modify)

线段树支持节点的动态修改。

对于如 "将节点(x)修改权值为(v)" 的指令，线段树可以以自下向上的方式修改。具体地，可以从根节点作为入口进入，递归向下找到需要修改的节点，再在回溯过程中更新沿路祖先节点的最值信息。时间复杂度(O(log_2n))。

(Code:)

inline void modify(int p,int x,int v)
{
	if(l(p)==r(p))//如果已经找到叶节点，更新权值
	{
		Max(p)=v;
		return;
	}
	int mid=(l(p)+r(p))/2;
	if(x<=mid)modify(p*2,x,v);//如果在左子树中，则递归左子树寻找
	if(x>mid)modify(p*2+1,x,v);//如果在右子树中，则递归右子树寻找
	Max(p)=max(Max(p*2),Max(p*2+1)); //回溯更新
}

查询 (query)

线段树还需要能够解决区间最值查询问题。

对于如 "查询区间([l,r])的最大值" 的指令，线段树可以递归查找得到最大值。具体地，从根节点开始，递归执行以下过程：

• 1.若([l,r])完全覆盖了当前结点所代表的区间，返回当前结点区间中的最大值作为备选答案
• 2.若左子节点与([l,r])有重合部分，递归访问左子节点
• 3.若右子节点与([l,r])有重合部分，递归访问右子节点

可以证明，区间查询的时间复杂度至多为(O(2log_2n))。

(Code:)

inline int query(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))return Max(p);//如果完全包含这个区间，返回这个区间的最大值作为备选答案
	int mid=(l(p)+r(p))/2;
	int res=-INF;
	//递归查询有重合部分的左右区间
	if(l<=mid)res=max(res,query(p*2,l,r));
	if(r>mid)res=max(res,query(p*2+1,l,r));
	return res;
}

至此，线段树的基本模型已经构成，我们通过一道模板题展示一下代码。

Description

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：
操作1：把 给定 第k1 个数改为k2;
操作2：查询 从第k1个数到第k2个数得最大值。（k1<=k2<=n）
所有的数都 <=100000

Input Format

第一行给定一个整数n，表示有n个操作。
以下接着n行，每行三个整数，表示一个操作。
第一个树表示操作序号，第二个数为k1，第三个数为k2

Output Format

若干行，查询一次，输出一次。

Sample Input

3
1 2 2
1 3 3
2 2 3

Sample Output

3

(Code:)

#include<bits/stdc++.h>
using namespace std;
const int N=100000+200,INF=0x3f3f3f3f;
int n;
struct SegmentTree
{
	int p,l,r,Max;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define p(x) tree[x].p
	#define Max(x) tree[x].Max
}tree[N*4];
inline void build(int p,int l,int r)
{
	l(p)=l,r(p)=r;
	if(l==r){Max(p)=0;return;}
	int mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	Max(p)=max(Max(p*2),Max(p*2+1));
}
inline void modify(int p,int x,int v)
{
	if(l(p)==r(p))
	{
		Max(p)=v;
		return;
	}
	int mid=(l(p)+r(p))/2;
	if(x<=mid)modify(p*2,x,v);
	if(x>mid)modify(p*2+1,x,v);
	Max(p)=max(Max(p*2),Max(p*2+1)); 
}
inline int query(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))return Max(p);
	int mid=(l(p)+r(p))/2;
	int res=-INF;
	if(l<=mid)res=max(res,query(p*2,l,r));
	if(r>mid)res=max(res,query(p*2+1,l,r));
	return res;
}
inline void input(void)
{
	scanf("%d",&n);
	build(1,1,n);
}
inline void solve(void)
{
	for(int i=1;i<=n;i++)
	{
		int index,k1,k2;
		scanf("%d%d%d",&index,&k1,&k2);
		if(index==1)modify(1,k1,k2);
		else printf("%d
",query(1,k1,k2)); 
	}
}
int main(void)
{
	input();
	solve();
	return 0;
} 

延迟标记 (lazytag)

在实现了简单的线段树后，我们考虑一下拓展。
我们以上实现的线段树是支持区间查询和单点修改的，如果需要区间修改呢？

如果用之前的线段树直接做的话，每一次修改的时间复杂度是(O(log_2n))，那么区间修改的时间复杂度将会达到至多(O(nlog_2n))，这是我们无法承受的。

我们可以考虑一下这种情况:对于一次区间修改指令([l,r,delta])(将([l,r])内的所有元素加(delta))，如果在之后的区间询问中完全没有调用到区间([l,r])，那么这次(O(nlog_2n))的修改就是完全无用的。

这样，我们对于每一个线段树中的节点引入一个变量(lazytag)延迟标记，(lazytag(x))代表(x)被已经某一次区间操作修改，但是(x)的子节点暂时还未修改，其修改的变化量为(lazytag(x))。然后，我们对于每一个区间修改操作，只对一个点做更新，并修改其(lazytag)值。需要查询时，我们再下传(lazytag)标记，顺带更新每一个沿路节点的关键值，就可以保证查询可以得到正确答案。

那么，每一次区间修改操作就只需要对(log_2n)个节点做修改，时间复杂度就优化到了(O(log_2n))，对于子节点的更新，只需要在查询时顺带更新即可。

(Code:)

struct SegmentTree
{
	int p,l,r,Max,lazytag;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define p(x) tree[x].p
	#define Max(x) tree[x].Max
	#define lazytag(x) tree[x].lazytag
}tree[N*4];
inline void spread(int p)
{
	if(lazytag(p))//将有标记节点的子节点更新，并下传标记
	{
		Max(p*2)+=lazytag(p);
		Max(p*2+1)+=lazytag(p);
		lazytag(p*2)+=lazytag(p);
		lazytag(p*2+1)+=lazytag(p);
		lazytag(p)=0;
	} 
} 
inline void modify(int p,int l,int r,int d)
{
	if(l<=l(p)&&r>=r(p))//包含修改区间，进行标记
	{
		Max(p)+=d;
		lazytag(p)+=d;
		return;
	}
	spread(p);//下传标记
	int mid=(l(p)+r(p))/2;
	if(l<=mid)modify(p*2,l,r,d);
	if(r>mid)modify(p*2+1,l,r,d);
	Max(p)=max(Max(p*2),Max(p*2+1)); 
}
inline int query(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))return Max(p);
	spread(p); //下传标记
	int mid=(l(p)+r(p))/2;
	int res=-INF;
	if(l<=mid)res=max(res,query(p*2,l,r));
	if(r>mid)res=max(res,query(p*2+1,l,r));
	return res;
}

通过一道例题展示一下区间修改线段树的代码。

Description

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：
操作1：将第k1 个数 到 第k2 个数加1；
操作2：查询 从第k1个数到第k2个数得最大值。（k1<=k2<=n）
所有的数都 <=100000

Input Format

第一行给定一个整数n，表示有n个操作。
以下接着n行，每行三个整数，表示一个操作。

Output Format

若干行，查询一次，输出一次。

Sample Input

3
1 2 2
1 3 3
2 2 3

Sample Output

1

(Code:)

#include<bits/stdc++.h>
using namespace std;
const int N=100000+200,INF=0x3f3f3f3f;
int n;
struct SegmentTree
{
	int p,l,r,Max,lazytag;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define p(x) tree[x].p
	#define Max(x) tree[x].Max
	#define lazytag(x) tree[x].lazytag
}tree[N*4];
inline void build(int p,int l,int r)
{
	l(p)=l,r(p)=r;
	if(l==r){Max(p)=0;return;}
	int mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	Max(p)=max(Max(p*2),Max(p*2+1));
}
inline void spread(int p)
{
	if(lazytag(p))
	{
		Max(p*2)+=lazytag(p);
		Max(p*2+1)+=lazytag(p);
		lazytag(p*2)+=lazytag(p);
		lazytag(p*2+1)+=lazytag(p);
		lazytag(p)=0;
	} 
} 
inline void modify(int p,int l,int r,int d)
{
	if(l<=l(p)&&r>=r(p))
	{
		Max(p)+=d;
		lazytag(p)+=d;
		return;
	}
	spread(p);
	int mid=(l(p)+r(p))/2;
	if(l<=mid)modify(p*2,l,r,d);
	if(r>mid)modify(p*2+1,l,r,d);
	Max(p)=max(Max(p*2),Max(p*2+1)); 
}
inline int query(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))return Max(p);
	spread(p); 
	int mid=(l(p)+r(p))/2;
	int res=-INF;
	if(l<=mid)res=max(res,query(p*2,l,r));
	if(r>mid)res=max(res,query(p*2+1,l,r));
	return res;
}
inline void input(void)
{
	scanf("%d",&n);
	build(1,1,n);
}
inline void solve(void)
{
	for(int i=1;i<=n;i++)
	{
		int index,k1,k2;
		scanf("%d%d%d",&index,&k1,&k2);
		if(index==1) modify(1,k1,k2,1);
		else printf("%d
",query(1,k1,k2));
	}
}
int main(void)
{
	input();
	solve();
	return 0;
} 

---

<后记>