Codeforces 85D Sum of Medians

传送门

D. Sum of Medians

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a1, a2, ..., ak}, where a1 < a2 < a3 < ... < ak, will be understood by as

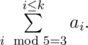
The 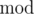 operator stands for taking the remainder, that is  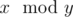stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 105), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 109.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

Sample test(s)

input

6
add 4
add 5
add 1
add 2
add 3
sum

output

3

input

14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum

output

5
11
13
-----------------------------------------------------------------------------------------------

Solution

用线段树维护集合

1.预处理所有add/del操作，将涉及的元素离散化为1...n

2.add x ，设x离散化为i，修改区间(i+1， n), 将各节点的sum[5]右移一位，再插入x

3.del x, 设x离散化为i, 修改区间(i+1, n), 将各节点的sum[5]左移一位, 在删除x

4.插入/删除元素需要知道元素在集合中的位置 (place),这由树状数组（BIT）维护。

5.对区间sum[5]的左移/右移操作需要用lazy-tag优化。

6.如果手写离散化，要注意实现细节。

7.需考虑极端输入，比如无sum询问的输入

---------------------------------------------------------------------------------------------

这是我第一发提交，TLE on test 5, 跪在极端输入上了，TLE的原因是调用了add(0, 1)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N=1e5+5;
#define X first
#define Y second
//BIT
int bit[MAX_N], rb;
int sum(int i){
    int s=0;
    while(i){
        s+=bit[i];
        i-=i&-i;
    }
    return s;
}
void add(int i, int x){
    while(i<=rb){
        bit[i]+=x;
        i+=i&-i;
    }
}

typedef pair<int, int> P;
P q[MAX_N];
int val[MAX_N];
char type[MAX_N][5];
int lisan(int N){
    int v;
    for(int i=0; i<N; i++){
        scanf("%s", type[i]);
        switch(*type[i]){
            case 'a':
            case 'd':
                scanf("%d", &v);
                q[i]=P(v, i);
                break; 
            case 's':
                q[i]=P(0, i);　　//TLE在这里
                break;
        }
    }
    sort(q, q+N);
    int ord=0;
    for(int i=0; i<N; ord++){
        val[ord]=q[i].X;
        do{
            q[i].X=ord;
            i++;
        }while(i<N&&q[i].X==val[ord]);
    }
    return ord;
}
bool cmp(const P &a, const P &b){
    return a.Y<b.Y;
}
//ST
struct node{
    int l, r, tag;
    ll sum[5];
    int mid(){return (l+r)>>1;}
}T[MAX_N<<2];
void shift(int id, int cnt){
    cnt%=5;
    if(!cnt) return;
    ll tmp[5];
    memcpy(tmp, T[id].sum, sizeof(tmp));
    for(int i=0; i<5; i++){
        int nt=(i+cnt+5)%5;
        T[id].sum[nt]=tmp[i];
    }
}
void pushdown(int id){
    node &now=T[id], &lch=T[id<<1], &rch=T[id<<1|1];
    lch.tag+=now.tag, rch.tag+=now.tag;
    shift(id<<1, now.tag);
    shift(id<<1|1, now.tag);
    now.tag=0;    //error prone
}
void unite(int id){
    node &now=T[id], &lch=T[id<<1], &rch=T[id<<1|1];
    for(int i=0; i<5; i++)
        now.sum[i]=lch.sum[i]+rch.sum[i];
}
void build(int id, int l, int r){
    node &now=T[id];
    T[id].l=l, T[id].r=r, T[id].tag=0;
    memset(T[id].sum, 0, sizeof(T[id].sum));
    if(l==r) return;
    int mid=(l+r)>>1;
    build(id<<1, l, mid);
    build(id<<1|1, mid+1, r);
}
void insert(int id, int pos, int ord, int v){
    node &now=T[id];
    if(now.l==now.r){
        now.sum[ord%5]+=v;
    }
    else{
        pushdown(id);
        if(pos<=now.mid())
            insert(id<<1, pos, ord, v);
        else
            insert(id<<1|1, pos, ord, v);
        unite(id);
    }
}
void shift(int id, int lb, int cnt){
    if(lb>rb) return;
    node &now=T[id];
    if(now.l>=lb){
        shift(id, cnt);
        now.tag+=cnt;    
    }
    else{
        pushdown(id);
        if(lb<=now.mid())
            shift(id<<1, lb, cnt);
        shift(id<<1|1, lb, cnt);
        unite(id);
    }
}

int main(){
    //freopen("in",  "r", stdin);
    int N;
    scanf("%d", &N);
    rb=lisan(N);
    build(1, 1, rb);
    sort(q, q+N, cmp);
    for(int i=0; i<N; i++){
        if(*type[i]=='a'){
            int ord=sum(q[i].X)+1;
            add(q[i].X, 1);
            shift(1, q[i].X+1, 1);
            insert(1, q[i].X, ord, val[q[i].X]);
        }
        else if(*type[i]=='d'){
            int ord=sum(q[i].X);
            add(q[i].X, -1);
            shift(1, q[i].X+1, -1);
            insert(1, q[i].X, ord, -val[q[i].X]);
        }
        else{
            printf("%I64d
", T[1].sum[3]);
        }
    }
    return 0;
}

其实我已经考虑到这种无sum询问的输入，但没注意到它会导致我的代码TLE

AC version

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N=1e5+5;
#define X first
#define Y second
//BIT
int bit[MAX_N], rb;
int sum(int i){
    int s=0;
    while(i){
        s+=bit[i];
        i-=i&-i;
    }
    return s;
}
void add(int i, int x){
    while(i<=rb){
        bit[i]+=x;
        i+=i&-i;
    }
}

typedef pair<int, int> P;
P q[MAX_N];
int val[MAX_N];
char type[MAX_N][5];
int lisan(int N){
    int v;
    for(int i=0; i<N; i++){
        scanf("%s", type[i]);
        switch(*type[i]){
            case 'a':
            case 'd':
                scanf("%d", &v);
                q[i]=P(v, i);
                break; 
            case 's':
                q[i]=P(INT_MAX, i);　　//注意这里的改动
                break;
        }
    }
    sort(q, q+N);
    int ord=0;
    for(int i=0; i<N;){
        ++ord;
        val[ord]=q[i].X;
        do{
            q[i].X=ord;
            i++;
        }while(i<N&&q[i].X==val[ord]);
    }
    return ord;
}
bool cmp(const P &a, const P &b){
    return a.Y<b.Y;
}
//ST
struct node{
    int l, r, tag;
    ll sum[5];
    int mid(){return (l+r)>>1;}
}T[MAX_N<<2];
void shift(int id, int cnt){
    cnt%=5;
    if(!cnt) return;
    ll tmp[5];
    memcpy(tmp, T[id].sum, sizeof(tmp));
    for(int i=0; i<5; i++){
        int nt=(i+cnt+5)%5;
        T[id].sum[nt]=tmp[i];
    }
}
void pushdown(int id){
    node &now=T[id], &lch=T[id<<1], &rch=T[id<<1|1];
    lch.tag+=now.tag, rch.tag+=now.tag;
    shift(id<<1, now.tag);
    shift(id<<1|1, now.tag);
    now.tag=0;    //error prone
}
void unite(int id){
    node &now=T[id], &lch=T[id<<1], &rch=T[id<<1|1];
    for(int i=0; i<5; i++)
        now.sum[i]=lch.sum[i]+rch.sum[i];
}
void build(int id, int l, int r){
    node &now=T[id];
    T[id].l=l, T[id].r=r, T[id].tag=0;
    memset(T[id].sum, 0, sizeof(T[id].sum));
    if(l==r) return;
    int mid=(l+r)>>1;
    build(id<<1, l, mid);
    build(id<<1|1, mid+1, r);
}
void insert(int id, int pos, int ord, int v){
    node &now=T[id];
    if(now.l==now.r){
        now.sum[ord%5]+=v;
    }
    else{
        pushdown(id);
        if(pos<=now.mid())
            insert(id<<1, pos, ord, v);
        else
            insert(id<<1|1, pos, ord, v);
        unite(id);
    }
}
void shift(int id, int lb, int cnt){
    if(lb>rb) return;
    node &now=T[id];
    if(now.l>=lb){
        shift(id, cnt);
        now.tag+=cnt;    
    }
    else{
        pushdown(id);
        if(lb<=now.mid())
            shift(id<<1, lb, cnt);
        shift(id<<1|1, lb, cnt);
        unite(id);
    }
}

int main(){
    //freopen("in",  "r", stdin);
    int N;
    scanf("%d", &N);
    rb=lisan(N);
    build(1, 1, rb);
    sort(q, q+N, cmp);
    for(int i=0; i<N; i++){
        if(*type[i]=='a'){
            int ord=sum(q[i].X)+1;
            add(q[i].X, 1);
            shift(1, q[i].X+1, 1);
            insert(1, q[i].X, ord, val[q[i].X]);
        }
        else if(*type[i]=='d'){
            int ord=sum(q[i].X);
            add(q[i].X, -1);
            shift(1, q[i].X+1, -1);
            insert(1, q[i].X, ord, -val[q[i].X]);
        }
        else{
            printf("%I64d
", T[1].sum[3]);
        }
    }
    return 0;
}