时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
在上一回中,小Hi和小Ho趁着便利店打折,买了一大堆零食。当他们结账后,看到便利店门口还有其他的活动。
店主:买了东西还可以参加游戏活动哦,如果能够完成游戏还有额外的奖品。
小Hi和小Ho赶紧凑了过去。
店主放了一块游戏板在店门口,有5行6列格子。左上角为坐标(1,1)。一部分格子是亮着的,另一部分是暗着的。

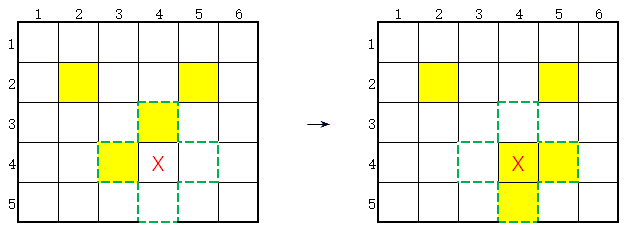
店主给出初始的状态,参加游戏的人员需要通过按下某些格子,让游戏板上所有的灯都亮起来就可以赢得奖品。
小Ho:这不就是开关灯问题么,看我来解决它!
本题改编自ACMICPC Greater New York 2002 EXTENDED LIGHTS OUT
输入
第1..5行:1个长度为6的字符串,表示该行的格子状态,1表示该格子是亮着的,0表示该格子是暗的。
保证一定存在解,且一定存在暗着的格子。
输出
需要按下的格子数量k,表示按下这k个位置后就可以将整个游戏板所有的格子都点亮。
接下来k行,每行一个坐标(x,y),表示需要按下格子(x,y)。x坐标较小的先输出,若x相同,则先输出y坐标较小的。
样例输入
001111 011111 111111 111110 111100
样例输出
2 1 1 5 6
- ---------------------------------------------------------------
- 异或方程组的形式为
- a[0][0]*x[0] ^ a[0][1]*x[1] ^ ... ^ a[0][n-1]*x[n-1] = a[0][n]
- a[1][0]*x[0] ^ a[1][1]*x[1] ^ ... ^ a[1][n-1]*x[n-1] = a[1][n]
- .
- .
- a[n-1][0]*x[0] ^ a[n-1][1]*x[1] ^ ... ^ a[n-1][n-1]*x[n-1] = a[n-1][n]
- 方程组中所有量都是bool量
- ----------------------------------------------------------------
- 比较异或方程组和一般的线性方程组,不难发现:
- 除了所有加号(+)都换成了异或(^)外,形式上两者是完全一致的
- 因而对于异或方程组,我们考虑是否可用类似于高斯消元解线性方程组的方法来解。
- 这就是说我们希望通过行变换将系数矩阵转化成单位矩阵。
- 对此我们有下述结论可用:
- ----------------------------------------------------------------------------------------
- 若
- a[0]*x[0] ^ a[1]*x[1] ^ ... ^ a[n-1]*x[n-1] = A
- b[0]*x[0] ^ b[1]*x[1] ^ ... ^ b[n-1]*x[n-1] = B
- 则
- (a[0]^b[0])*x[0] ^ (a[1]^b[1])*x[1] ^ ... ^ (a[n-1]^b[n-1])*x[n-1] = A ^ B
- -----------------------------------------------------------------------------------------
- 实际上我们只要证明
- a*x ^ b*x = (a ^ b)*x
- 上述结论便是很自然的推论了
- 而由于这里涉及的所有量都是bool值,只要枚举便能证明。
- 我们也可以从另一角度来看:
- 异或运算相当于模2下的加法运算,即
- a ^ b = (a + b) % 2
- 我们有
- (a*x + b*x) % 2
- = ((a+b)*x) % 2
- = ((a+b) % 2) * (x % 2) % 2
- 在 a, b, x都是bool量的情况下
- 上式即
- a*x ^ b*x = (a ^ b)*x
- 这样异或(^)与加法(+)两种运算便自然联系起来了,异或方程组与一般的线性方程组本质上没有区别。
- --------------------------------------------------------------------------------------------------------
- 异或方程组的高斯消元过程同样是:
- 枚举行,对第i行,在第i列选主元交换到第i行。将其余该列为1的行,用第i行与之异或。
- --------------------------------------------------------------------------------------------------------
#include <bits/stdc++.h> using namespace std; char s[5][7]; int a[30][31]; int dx[]={0, 0, 0, 1, -1}; int dy[]={0, 1, -1, 0, 0}; int ok(int x, int y){ return x>=0&&x<5&&y>=0&&y<6; } int swap(int i, int j){ int tmp[31]; memcpy(tmp, a[i], sizeof(tmp)); memcpy(a[i], a[j], sizeof(tmp)); memcpy(a[j], tmp, sizeof(tmp)); } int gauss(int n){ for(int i=0; i<n; i++){ for(int j=i; j<n; j++) if(a[j][i]){ swap(i, j); break; } for(int j=0; j<n; j++) if(j!=i&&a[j][i]){ //消去第j行第i项 for(int k=i; k<=n; k++) a[j][k]^=a[i][k]; } //output(); } } int main(){ for(int i=0; i<5; i++) cin>>s[i]; for(int i=0; i<5; i++) for(int j=0; j<6; j++){ int now=6*i+j; for(int k=0; k<5; k++){ int x=i+dx[k], y=j+dy[k]; if(ok(x, y)){ int nei=6*x+y; a[now][nei]=1; } } a[now][30]=(s[i][j]-'0')^1; } gauss(30); int ans=0; for(int i=0; i<30; i++) ans+=a[i][30]; cout<<ans<<endl; for(int i=0; i<30; i++) if(a[i][30]) cout<<i/6+1<<' '<<i%6+1<<endl; }