LGP5075【JSOI2012】分零食

、

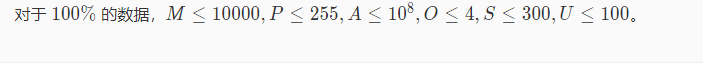
• 题解：

  • 令$F$为欢乐度$f(x) = Ox^2 + Sx + U$的生成函数，常数项为$0$；
  • 令$G(x) = sum_{i=0}^{A} F^i (x) $
    
  • $ans = [x^M]G;$
  • 模数比较麻烦所以我用的分治求:
    
  • 如果现在要求$0$到$n-1$的$G_{n} = sum_{i=0}^{n-1}F^{i}$和$F_{n} = F^{n} $，假设n为偶数；
  • 那么分治求出关于$n/2$的答案$G_{frac{n}{2}}$和$F_{frac{n}{2}}$
  • $$G_{n} = (F_{frac{n}{2}}+1)G_{frac{n}{2}}  , F_{n} = F_{frac{n}{2}}^2$$
  • 如果$n$是奇数先算用上述操作算$n-1$，再把$F_{n-1}$补加给$G_{n-1}$得到$G_{n}$,最后$F_{n-1}$另外乘一次得到$F_{n}$；
  • 和快速幂的思想差不多；

  • #include<bits/stdc++.h>
    #define ld double
    using namespace std;
    const int N=40010;
    const ld pi=acos(-1);
    int M,P,A,O,S,U,len,L,rev[N];
    struct C{
        ld x,y;
        C(ld _x=0,ld _y=0):x(_x),y(_y){};
        C operator +(const C&A)const{return C(x+A.x,y+A.y);}
        C operator -(const C&A)const{return C(x-A.x,y-A.y);}
        C operator *(const C&A)const{return C(x*A.x-y*A.y,x*A.y+y*A.x);}
        C operator /(const ld&A)const{return C(x/A,y/A);}
    }f[N],g[N],t[N];
    int cal(int x){return (O*x*x+S*x+U)%P;}
    void fft(C*a,int f){
        for(int i=0;i<len;++i)if(i<rev[i])swap(a[i],a[rev[i]]);
        for(int i=1;i<len;i<<=1){
            C wn=C(cos(pi/i),f*sin(pi/i));
            for(int j=0;j<len;j+=i<<1){
                C w=C(1,0);
                for(int k=0;k<i;++k,w=w*wn){
                    C x=a[j+k],y=w*a[j+k+i];
                    a[j+k]=x+y,a[j+k+i]=x-y;
                }
            }
        }
        if(!~f)for(int i=0;i<len;++i){
            a[i]=a[i]/len;
            a[i].x=int(a[i].x+0.1)%P;
            a[i].y=0;
        }
    }
    void solve(int A){
        if(A==1){g[0].x=1;return;}
        solve(A>>1);
        fft(f,1);fft(g,1);
        for(int j=0;j<len;++j)g[j]=g[j]*(f[j]+C(1,0)),f[j]=f[j]*f[j];
        fft(f,-1);fft(g,-1);
        for(int j=M+1;j<len;++j)f[j].x=g[j].x=0; 
        if(A&1){
            for(int j=0;j<=M;++j)g[j].x=(int)(g[j].x+f[j].x+0.1)%P; 
            fft(f,1);for(int j=0;j<len;++j)f[j]=f[j]*t[j];
            fft(f,-1);for(int j=M+1;j<len;++j)f[j].x=0;
        }
    }
    int main(){
    //    freopen("P5075.in","r",stdin);
    //    freopen("P5075.out","w",stdout);
        scanf("%d%d%d%d%d%d",&M,&P,&A,&O,&S,&U);
        for(int i=1;i<=M;++i)t[i].x=f[i].x=cal(i%P);
        for(len=1;len<=M<<1;len<<=1,L++);
        for(int i=0;i<len;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
        fft(t,1);solve(min(A,M)+1);
        printf("%d
    ",(int)(g[M].x+0.1)%P);
        return 0;
    }