动态点分治
先看一道题目 [ZJOI2007]捉迷藏
显然如果不带修改O(N)的树形动规和O(NlogN)的静态点分治都可以切掉这道题
一、点分树
考虑点分治,对于每一个分治区域树的重心的答案只会与其所有子区域树有关,所以我们可以再构建一颗点分树:
在点分治的过程中,我们把每个区域树的重心和其子区域树的重心建立父子关系,形成了一颗新的树,称为点分树。
点分树的性质:1、一颗点分树的深度为严格logN的
2、当修改一个结点事,只会对其父亲结点造成影响z
二、维护结点信息
对于这道题,我们只需维护每个结点上的最大链和次大链,我们可以对于每个结点建两个大根堆:
A:关键字:原分治区域树中以该结点为链的一段的所有链的长度
B:关键字:原分治树中以该结点为根时,每个子树中最长链的长度
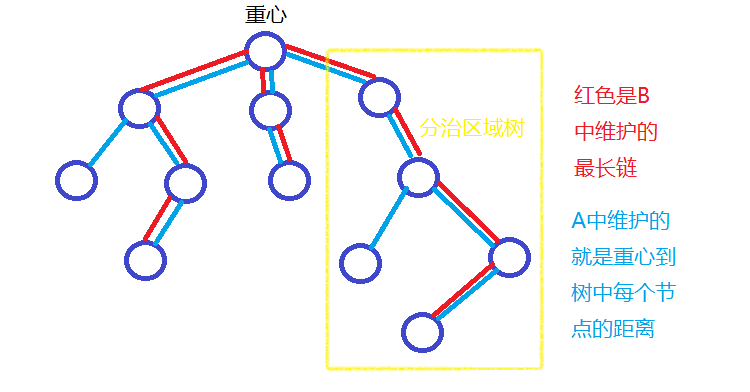
所以我们可以得出每个分支区域树中,B中的第一大元素和第二大元素的和即是答案
B由该结点为根的子树中每个A的最大值组成
最后我们只需用树链剖分求lca,并用差分求树上任意两点距离即可
三、时间复杂度&空间复杂度
时间复杂度为点分治的NlogN+堆的logN == O(Nlog2N)
空间复杂度:O(N)
1 #include<bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define MAXN 100010 4 using namespace std; 5 inline int read () 6 { 7 int w=1,s=0; 8 char ch=getchar (); 9 while (ch<'0'||ch>'9'){if (ch=='-') w=-1;ch=getchar ();} 10 while ('0'<=ch&&ch<='9') s=(s<<1)+(s<<3)+(ch^48),ch=getchar (); 11 return s*w; 12 } 13 struct Heap{ 14 priority_queue<int>A,B;int size; 15 Heap(){size=0;} 16 void push (int x){A.push (x),size++;} 17 void pop (int x){B.push (x),size--;} 18 int top (){while (!B.empty ()&&A.top ()==B.top ()) A.pop (),B.pop ();return size?A.top ():-INF;} 19 int len () 20 { 21 if (size==0) return -1; 22 if (size==1) return 0; 23 int x=top ();pop (x);int y=top ();push (x); 24 return x+y; 25 } 26 void op (int x,int c){c?pop (x):push (x);} 27 }a[MAXN],b[MAXN],ans; 28 struct edge{ 29 int v,w,nxt; 30 }e[MAXN<<1]; 31 int n,q,cnt,root,sum,tot; 32 int head[MAXN],size[MAXN],maxp[MAXN],s[MAXN],col[MAXN]; 33 int Fa[MAXN],dep[MAXN],son[MAXN],dist[MAXN],top[MAXN]; 34 bool used[MAXN]; 35 char opt[MAXN]; 36 void add (int u,int v,int w) 37 { 38 e[++cnt].v=v,e[cnt].w=w,e[cnt].nxt=head[u],head[u]=cnt; 39 } 40 void dfs1 (int u,int fa) 41 { 42 Fa[u]=fa,size[u]=1,dep[u]=dep[fa]+1; 43 for (int i=head[u];i!=0;i=e[i].nxt) 44 if (e[i].v!=fa) 45 { 46 dist[e[i].v]=dist[u]+e[i].w; 47 dfs1 (e[i].v,u); 48 size[u]+=size[e[i].v]; 49 if (size[e[i].v]>size[son[u]]) son[u]=e[i].v; 50 } 51 } 52 void dfs2 (int u,int topf) 53 { 54 top[u]=topf; 55 if (son[u]) dfs2 (son[u],topf); 56 for (int i=head[u];i!=0;i=e[i].nxt) 57 if (e[i].v!=Fa[u]&&e[i].v!=son[u]) 58 dfs2 (e[i].v,e[i].v); 59 } 60 int lca (int x,int y) 61 { 62 while (top[x]]!=top[y]) 63 { 64 if (dep[top[x]]<dep[top[y]]) swap (x,y); 65 x=Fa[top[x]]; 66 } 67 return dep[x]<dep[y]?x:y; 68 } 69 void getrt (int u,int fa) 70 { 71 size[u]=1,maxp[u]=0; 72 if (!col[u]) s[++tot]=u; 73 for (int i=head[u];i!=0;i=e[i].nxt) 74 if (e[i].v!=fa&&!used[e[i].v]) 75 { 76 getrt (e[i].v,u); 77 size[u]+=size[e[i].v]; 78 maxp[u]=max (maxp[u],size[e[i].v]); 79 } 80 maxp[u]=max (maxp[u],sum-size[u]); 81 if (maxp[u]<maxp[root]) root=u; 82 } 83 int f[MAXN]; 84 int getdis (int x,int y) 85 { 86 return dist[x]+dist[y]-(dist[lca (x,y)]<<1); 87 } 88 int divide (int u) 89 { 90 used[u]=1;if (!col[u]) b[u].push (0); 91 for (int i=1;i<=tot;i++) a[u].push (getdis (f[u],s[i])); 92 for (int i=head[u];i!=0;i=e[i].nxt) 93 if (!used[e[i].v]) 94 { 95 maxp[root=tot=0]=sum=size[e[i].v],getrt (e[i].v,0); 96 f[root]=u; 97 int child=divide (root); 98 b[u].push (a[child].top ()); 99 } 100 ans.push (b[u].len ()); 101 return u; 102 } 103 void modify (int x,int c) 104 { 105 int l1=b[x].len (),l2,s1,s2;b[x].op (0,c); 106 if (l1!=(l2=b[x].len ())) ans.pop (l1),ans.push (l2); 107 for (int u=x,fa=f[u];fa;fa=f[u=fa]) 108 { 109 s1=a[u].top (),a[u].op (getdis (fa,x),c),s2=a[u].top(); 110 if (s1!=s2) 111 { 112 l1=b[fa].len (); 113 if (s1!=-INF) b[fa].pop (s1); 114 if (s2!=-INF) b[fa].push (s2); 115 l2=b[fa].len (); 116 if (l1!=l2) ans.pop (l1),ans.push (l2); 117 } 118 } 119 } 120 int main() 121 { 122 n=read (); 123 for (int i=1;i<n;i++) 124 { 125 int u=read (),v=read (); 126 add (u,v,1);add (v,u,1); 127 } 128 dfs1 (1,0);dfs2 (1,1); 129 maxp[root]=sum=n,getrt (1,0); 130 divide (root); 131 q=read (); 132 while (q--) 133 { 134 scanf ("%s",opt+1); 135 if (opt[1]=='C') 136 { 137 int x=read ();col[x]^=1; 138 modify (x,col[x]); 139 } 140 else printf ("%d ",ans.top ()); 141 } 142 return 0; 143 }