题意
思路
一个数如果要作为指数,那么它不能直接对模数取模,这是常识;
诸如 (c^{c^{c^{c..}}}) 的函数递增飞快,不是高精度可以描述的,这也是常识。
所以,此题要用到很多数论知识。
欧拉函数
定义
(varphi(n)) 为 ([1,n]) 中与 (n) 互质的正整数个数(包括 (1))。
通式
(displaystyle varphi(n)=nprod_{p|n}(1-{1over p})) 其中 (p) 为 (x) 的质因子。
如何理解这个式子呢?可以粗略这样理解:(displaystyle (1-{1over p})) 意思就是筛掉所有能被 (p) 整除的数,当然这种理解方法是错误的,只能算是感性理解,方便记忆。
前几项
摘自维基百科:
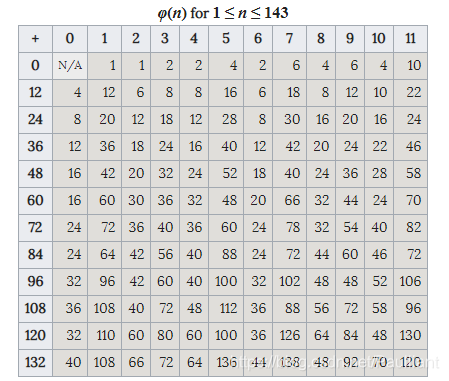
性质
几条比较重要的性质:
若 (gcd(m,n)=1),有 (varphi(mn)=varphi(m)varphi(n))
令 (m=2),不难得出当 (n) 为奇数时,(varphi(2n)=varphi(n))
另外,对于质数 (p),有 (varphi(p)=p-1)
欧拉定理
(a^{varphi(n)} equiv 1 pmod n) 其中 (gcd(a,n)=1)
(n) 为质数的情况就是著名的费马小定理。
扩展欧拉定理
扩展欧拉定理把幂的层数和模数都降了下来,用它就可以解决本题了。
回归本题
先考虑暴力做法再尝试优化。我们可以给每个数一个标记,表示多少层 (c) 上才是 (a_i)。然后每次只需计算这个 (c^{c^{c^{...^{a_i}}}}) 即可。
套用扩展欧拉定理,假设标记为 (3),就是计算(c^{c^{c^{a_i}}} mod p) 的值。
分两类讨论,当 (c^{c^{a_i}}<varphi(p)),问题就转化成了求 (c^{c^{a_i}}mod varphi(p)) 的值;否则,只需在此基础上加 (varphi(p)) 即可,而判断大小只需在快速幂上传一个标记就行了。
一路递归下去,当模数变成 (1) 时直接返回 (0) 即可。
考虑优化。由于模数给定,那么变化显然是从 (p) 到 (varphi(p)) 再到 (varphi(varphi(p))) 这样一路变化的。变化不会超过 (log p) 层,那么总标记次数就不超过 (nlog p) 次。
可以用线段树维护一个区间,那么再修改一个区间时,也维护一个区间的最小修改次数的最大值,当它对应的模数已经是 (1) 时,便不进行修改。再修改时,要算出 (c^{c^{c^{...^{a_i}}}}) 的值,最多修改 (nlog n) 次,最深又有 (log) 层,算快速幂又有一个 (log)。三个 (log) 是过不了本题的。
然而快速幂可以直接分块预处理,由于模数不超过 (log n) 个,则分别预处理
(c^{i} mod p_k,c^{50000i} mod p_k) 的值,以及和 (p_k) 的大小关系即可。复杂度降至两个 (log)
查询直接区间求和,一个 (log)。
代码
#include<bits/stdc++.h>
#define FOR(i,x,y) for(int i=(x),i##END=(y);i<=i##END;++i)
#define DOR(i,x,y) for(int i=(x),i##END=(y);i>=i##END;--i)
typedef long long LL;
using namespace std;
const int N=5e4+5;
const int _N=5e4;
int P[105],a[N],tot,n,m,c;
LL PW[2][N][105];bool FL[2][N][105];
//PW[i][j][k] c^(i*_N+j)%P[k]
//FL[i][j][k] [c^(i*_N+j)>=P[k]]
LL phi(LL n)
{
LL res=n;
for(LL i=2;i*i<=n;i++)if(n%i==0)
{
res=res/i*(i-1);
while(n%i==0)n/=i;
}
if(n>1)res=res/n*(n-1);
return res;
}
struct node
{
int Mi,sum;
node operator +(const node &_)const
{
return (node){min(Mi,_.Mi),(sum+_.sum)%P[0]};
}
}nd[N<<2];
void build(int k,int l,int r,int *arr)
{
if(l==r)
{
nd[k].Mi=0;
nd[k].sum=arr[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid,arr);
build(k<<1|1,mid+1,r,arr);
nd[k]=nd[k<<1]+nd[k<<1|1];
}
LL Pow(LL p,int id,bool &flag)//c^p%P[id] flag=[c^p>=P[id]]
{
flag=FL[0][p%_N][id]||FL[1][p/_N][id]||(PW[0][p%_N][id]*PW[1][p/_N][id]>=P[id]);
return PW[0][p%_N][id]*PW[1][p/_N][id]%P[id];
}
LL calc(int x,LL y)
{
if(y>=P[x])y=y%P[x]+P[x];
DOR(i,x,1)
{
bool flag;
y=Pow(y,i-1,flag);
if(flag)y+=P[i-1];
}
return y%P[0];
}
void update(int k,int L,int R,int l,int r)
{
if(L<=l&&r<=R&&nd[k].Mi>=tot)return;
if(l==r)
{
nd[k].sum=calc(++nd[k].Mi,a[l]);
return;
}
int mid=(l+r)>>1;
if(L<=mid)update(k<<1,L,R,l,mid);
if(R>mid)update(k<<1|1,L,R,mid+1,r);
nd[k]=nd[k<<1]+nd[k<<1|1];
}
int query(int k,int L,int R,int l,int r)
{
if(L<=l&&r<=R)return nd[k].sum;
int mid=(l+r)>>1;
if(R<=mid)return query(k<<1,L,R,l,mid);
else if(L>mid)return query(k<<1|1,L,R,mid+1,r);
else return (query(k<<1,L,R,l,mid)+query(k<<1|1,L,R,mid+1,r))%P[0];
}
void pre_compute()
{
FOR(i,0,tot)
{
PW[0][0][i]=1,FL[0][0][i]=(1>=P[i]);
FOR(j,1,_N)
{
PW[0][j][i]=PW[0][j-1][i]*c;
FL[0][j][i]=FL[0][j-1][i]|(PW[0][j][i]>=P[i]);
if(PW[0][j][i]>=P[i])PW[0][j][i]%=P[i];
}
PW[1][0][i]=1,FL[1][0][i]=(1>=P[i]);
FOR(j,1,_N)
{
PW[1][j][i]=PW[1][j-1][i]*PW[0][_N][i];
FL[1][j][i]=FL[1][j-1][i]|(PW[1][j][i]>=P[i]);
if(PW[1][j][i]>=P[i])PW[1][j][i]%=P[i];
}
}
}
int main()
{
scanf("%d%d%d%d",&n,&m,&P[tot=0],&c);
FOR(i,1,n)scanf("%d",&a[i]);
while(P[tot]!=1)
{
P[tot+1]=phi(P[tot]);
tot++;
}
P[++tot]=1;
pre_compute();
build(1,1,n,a);
while(m--)
{
int op,l,r;
scanf("%d%d%d",&op,&l,&r);
if(op==0)update(1,l,r,1,n);
else printf("%d
",query(1,l,r,1,n));
}
return 0;
}