2021牛客寒假 第一场

A-串

法一：动态规划构造法

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ll long long
#define MAX 1000001
const int N = 5e6+7;
const int MOD = 1e9+7;
using namespace std;
ll dp[N][5]={0},n,ans;
int main(){
    scanf("%d",&n);
    dp[1][0]=25;//前i中不含u的数量 
    dp[1][1]=1;//前i中含u不含s的数量 
    dp[1][2]=0;//前i中含u又含s的数量 
    for(int i=2;i<=n;++i){
        dp[i][0]=(dp[i-1][0]*25)%MOD;//等于前i-1中的不含u的数量拼上除了u以外的25个字母 
        dp[i][1]=(dp[i-1][0]+dp[i-1][1]*25)%MOD;//等于i-1中的不含u的数量拼一个u，再加上前i-1中含u不含s的数量除了s以外的25个字母   
        dp[i][2]=(dp[i-1][1]+dp[i-1][2]*26)%MOD;//等于前i-1中含u不含s的数量拼一个s，再加上前i-1中含u又含s的数量拼上任意字母 
    }
    for(int i=2;i<=n;++i)//计算所有前i的总和 
        ans=(ans+dp[i][2])%MOD;
    printf("%d
",ans);
    return 0;
}

法二：容斥

设dp[len]为长度为len且包含us的字符串数量

那么dp[len]可以由dp[len-1]*26转化而来

也可以由前len-1长度中只包含u不包含s的数量加上len位的s转化而来

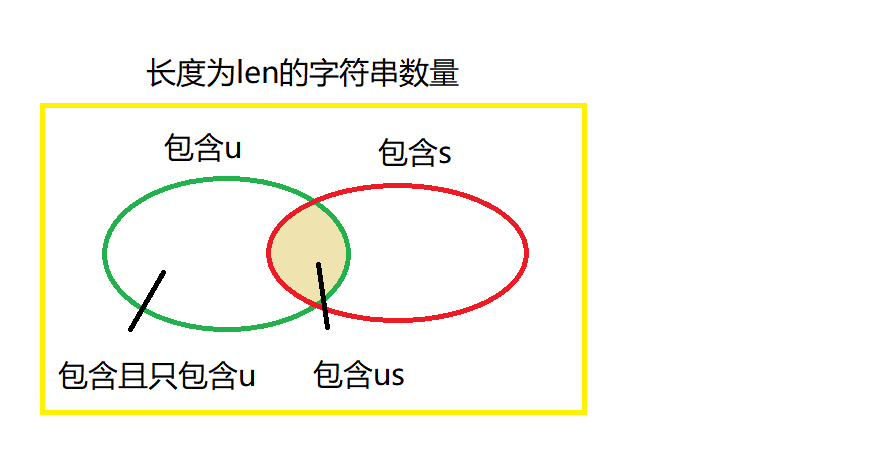
那么包含且只包含u的数量为 总数26^len - 不含u的部分25^len - 包含了us的部分dp[len-1]

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ll long long
#define MAX 1000001
const int N = 5e6+7;
const int MOD = 1e9+7;
using namespace std;
ll dp[N]={0},n,ans;
ll qpow(ll x,ll y){
    ll res=1;
    x=x%MOD;
    while(y){
        if(y&1)res=res*x%MOD;
        x=x*x%MOD;
        y>>=1;
    }
    return res%MOD;
}
int main(){
    scanf("%d",&n);
    dp[2]=1;
    for(int i=3;i<=n;++i){
        dp[i]=(dp[i-1]*26)%MOD;
        dp[i]=(dp[i]+qpow(26,i-1)-qpow(25,i-1)-dp[i-1]+MOD)%MOD;
    } 
    ll ans=0;
    for(int i=2;i<=n;++i){
        ans=(ans+dp[i])%MOD;
    }
    printf("%lld
",ans); 
    return 0;
}

I-限制不互素对的排列

注意0<=k<=n/2

最大化不互素的个数就是偶数之间

发现n<6&&k==n/2的时候，没有合适的数列

n>=6&&k==n/2的时候可以用3 6 接上偶数来完成这个喜加一的过程

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ll long long
#define MAX 1000001
const int N = 5e6+7;
const int MOD = 1e9+7;
using namespace std;
int vis[N]={0},n,k;
int main(){
    scanf("%d%d",&n,&k);
    if(n<6&&k==n/2){
        cout<<"-1"<<endl;
        return 0;
    }
    if(k==n/2){
        printf("3 ");
        printf("6 "); 
        vis[3]=1;
        vis[6]=1;
        for(int i=1;i<=k;++i){
            if(vis[i*2]==1)    continue;
            printf("%d ",i*2);
            vis[i*2]=1;
        }
        for(int i=1;i<=n;++i){
            if(vis[i]==0)    printf("%d ",i);
        }
    }
    else{
        for(int i=1;i<=k+1;++i){
            printf("%d ",i*2);
            vis[i*2]=1;
        }
        for(int i=1;i<=n;++i){
            if(vis[i]==0)    printf("%d ",i);
        }
    }
    return 0;
}