【问题描述】
在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其它方格不同,则称该方格为一特殊方格,称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ,有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。
 图一
图一
在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k * 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。现给出棋盘的大小和特殊方格所在的位置,请找出这种棋盘。
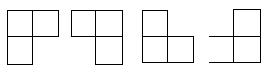 图二
图二
【样例输入】
2
0 0
【样例输出】
0 1
1 1
【解题思路】
初看时感觉这题目很难,我们可以利用分治的思想,像图一一样,将一个大棋盘不断分成四个部分,直至每个部分只包含一个方格,那么递归的边界就出来了。然后对于每一个部分,我们需要找到特殊方格,就需要查看这个特殊方格是否在我们现在找的这个范围,如果在,就继续找,不在,就将其对称的部分用L型牌覆盖,然后找该编号的L型牌覆盖的区域。详见代码。
【代码实现】
1 var tile,size,k,i,x,y,j:longint; 2 a:array[-1..100,-1..100] of longint; 3 procedure try(tr,tc,dr,dc,size:longint); 4 var s,t:longint; 5 begin 6 if size=1 then 7 exit; 8 t:=tile;//L型牌的编号 9 inc(tile); 10 s:=size div 2; 11 if (dr<tr+s)and(dc<tc+s) then//查找是否在左上角,在,继续找 12 try(tr,tc,dr,dc,s) 13 else//不在,将右下角用L型牌覆盖,找该L型牌 14 begin 15 a[tr+s-1,tc+s-1]:=t; 16 try(tr,tc,tr+s-1,tc+s-1,s); 17 end; 18 if (dr<tr+s)and(dc>=tc+s) then//查找是否在右上角 19 try(tr,tc+s,dr,dc,s) 20 else//不在将左下角用L型牌覆盖 21 begin 22 a[tr+s-1,tc+s]:=t; 23 try(tr,tc+s,tr+s-1,tc+s,s); 24 end; 25 if (dr>=tr+s)and(dc<tc+s) then//查找是否在左下角 26 try(tr+s,tc,dr,dc,s) 27 else//不在将右上角用L型牌覆盖 28 begin 29 a[tr+s,tc+s-1]:=t; 30 try(tr+s,tc,tr+s,tc+s-1,s); 31 end; 32 if (dr>=tr+s)and(dc>=tc+s) then//查找是否在右下角 33 try(tr+s,tc+s,dr,dc,s) 34 else//不在将左上角用L型牌覆盖 35 begin 36 a[tr+s,tc+s]:=t; 37 try(tr+s,tc+s,tr+s,tc+s,s); 38 end; 39 end; 40 begin 41 readln(size); 42 readln(x,y); 43 tile:=1; 44 try(0,0,x,y,size); 45 for i:=0 to size-1 do 46 begin 47 for j:=0 to size-1 do 48 write(a[i,j]:3,' '); 49 writeln; 50 end; 51 end.