四、基本几何变换
图形的几何变换是指对图形的几何信息经过平移、比例、旋转、等变换后产生新的图形。
1、平移变换
平移是一种【不产生变形】而移动物体的【刚体变换】,即物体上的每个点移动相同数量的坐标。下图是点P(x,y)平移到P*(x*,y*).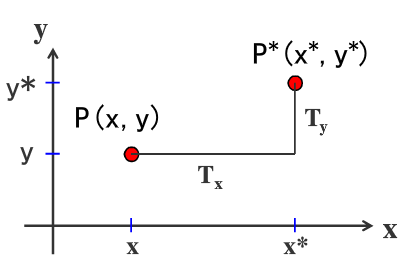

齐次坐标的计算形式为:
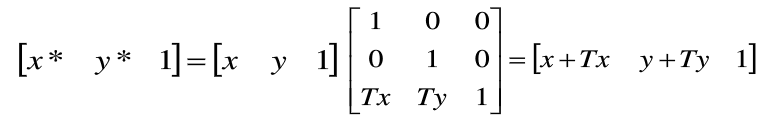
Tx,Ty称为【平移矢量】
2、比例变换
比例变换是指对P点相对于坐标原点沿x轴方向缩放Sx倍,沿y方向缩放Sy倍,其中Sx,Sy称为比例系数,可以赋予任何【正整数】,值小于1缩小物体的尺寸,值大于1则放大物体,都指定为1,物体尺寸就不会改变。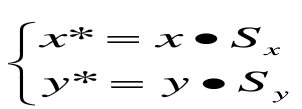
齐次坐标的计算形式为: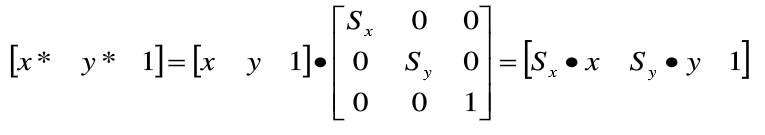
3、对称变换
对称变换也称为反射变换或镜像变换,变换后的图形是原图形关于一轴线或原点的镜像。
(1)关于x轴对称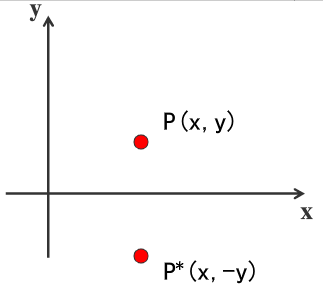
齐次坐标的计算形式为:
(2)关于y轴对称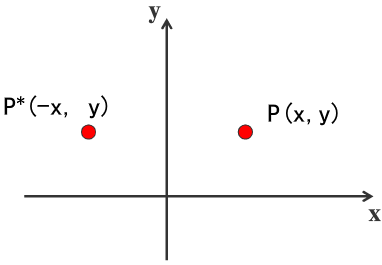
齐次坐标的计算形式为:
4、旋转变换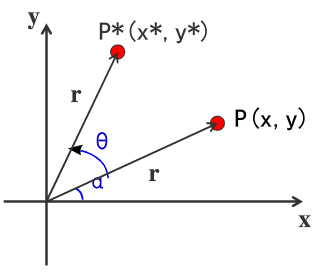
首先确定当基准点为坐标原点时,点位置P旋转的变换方程,应用标准三角特性,利用角度α,θ将转换后的坐标表示为: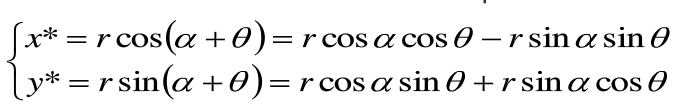
在极坐标系中点的原始坐标为:
将x,y代入上式,就得到相对于原点将在位置(x,y)处的点旋转θ角的变换方程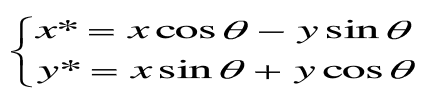
二维图形绕原点【逆】时针旋转θ角的齐次坐标计算式可写为: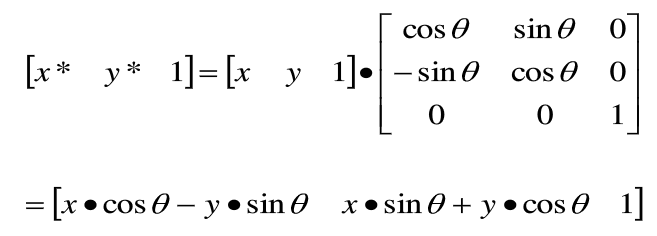
二维图形绕原点【顺】时针旋转θ角的齐次坐标计算式可写为: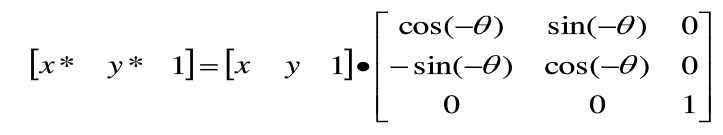
5、错切变换
在图形学的应用中,有时需要产生弹性物体的变形处理,这就需要用到错切变换。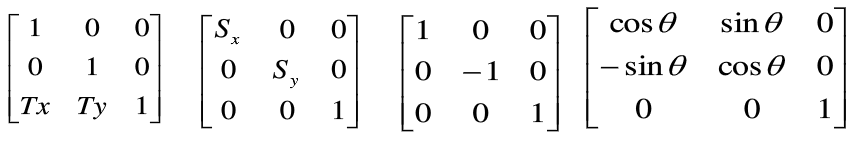
变换矩阵中的非对角线元素大都为零,若变换矩阵中的非对角元素不为0,则意味着x,y同时对图形的变换起作用。也就是说。变换矩阵中非对角线元素起着把图形沿x方向或y方向错切的作用。
x值或y值越小,错切量越小;x值或y值越大,错切量越大。其变换矩阵为: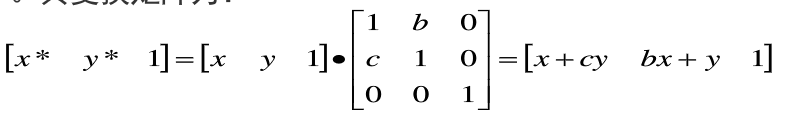
(1)沿x方向错切
当b=0时,有:

四、复合变换
复合变换就是指图形作一次以上的几何变换,变换结果是每次的【变换矩阵相乘】。
——>任何一个复杂的几何变换都可以看作基本几何变换的组合形式。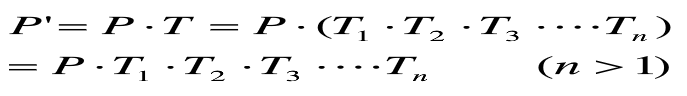
(1)二维复合平移
p点经过两次【连续】的平移后,其变换矩阵可写为: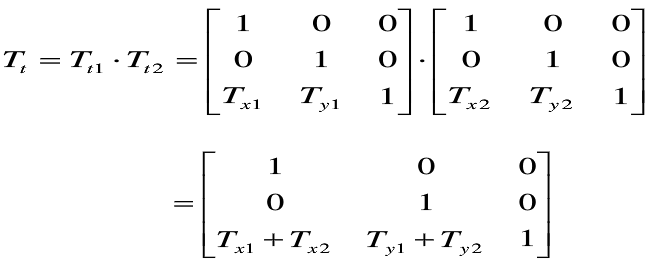
(2)二维复合比例平移
p点经过两个【连续】比例变换后,其变换矩阵可写为: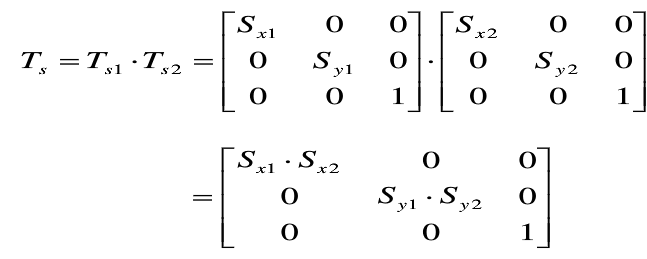
——>两个连续比例变换是相乘的
(3)二维复合旋转
p点经过两个【连续】旋转变换后,其变换矩阵可写为: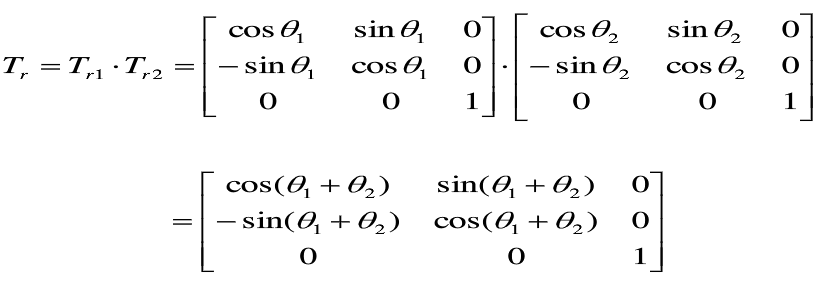
——>两个连续旋转是相加的
【注意:矩阵乘法不满足交换率】
(4)坐标系之间的变换
eg:下图显示了两个笛卡尔坐标系xoy和x'o'y',而o'点在xoy坐标系的(x0,y0)处,为了将p(xp,yp)点从xoy坐标系变换到x'o'y'坐标系如何进行计算?
可分为两步进行:
1>将x'o'y'坐标系的原点平移至xoy坐标系的原点——平移变换
2>将x'轴旋转到x轴上——旋转变换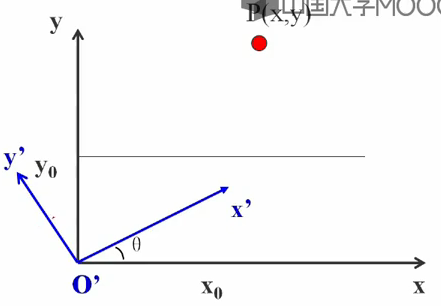
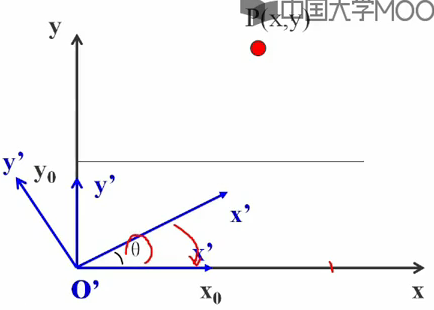
变换矩阵表示为:
(5)相对任意参考点的二维几何变换
比例、旋转变换等均与参考点相关,变换过程如下:
a、将固定点移至坐标原点,此时进行平移变换
b、针对原点进行二维几何变换
c、进行反平移,将固定点又移回原来的位置
五、二维变换矩阵
二维空间中某点的变化可以表示成点的齐次坐标与3阶的二维变换矩阵T2d相乘,即:
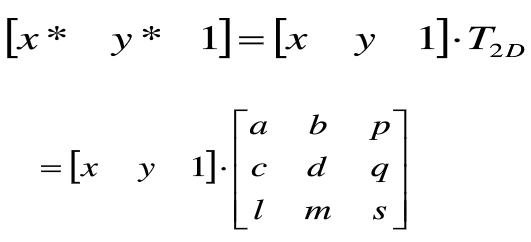

六、二维几何变换的计算
(1)点的变换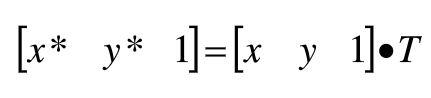
(2)直线的变换
直线的变换可以通过对直线两端点进行变换,从而改变直线的位置和方向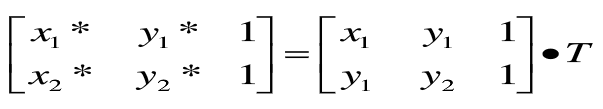
(3)多边形的变换
多边形的变换是将变换矩阵作用到【每个顶点】的坐标位置,并按新的顶点坐标值和当前属性设置来生成新的多边形。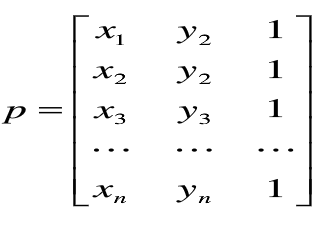
七、窗口视区变换
1、窗口和视区
【世界坐标系中】要显示的区域称为窗口,窗口定义显示什么。
窗口映射到【显示器(设备)上】的区域称为视区,视区定义在何处显示。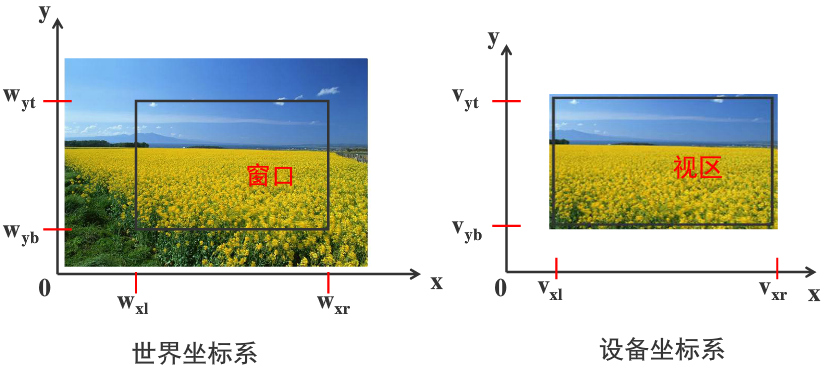
世界坐标系中的一个窗口可以对应于多个视区。
2、观察变换
(1)变焦距效果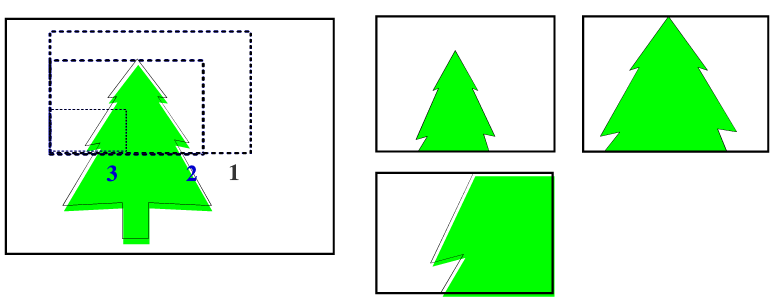
当窗口变小时,由于【视区大小不变】,就可以放大图形对象的某一部分,从而观察到在较大的窗口时未显示出的细节。
——>类似于照相机的变焦处理
(2)整体缩放效果
当窗口大小不变而视区大小发生变化时,得到整体放缩效果,这种放缩【不改变】观察对象的内容。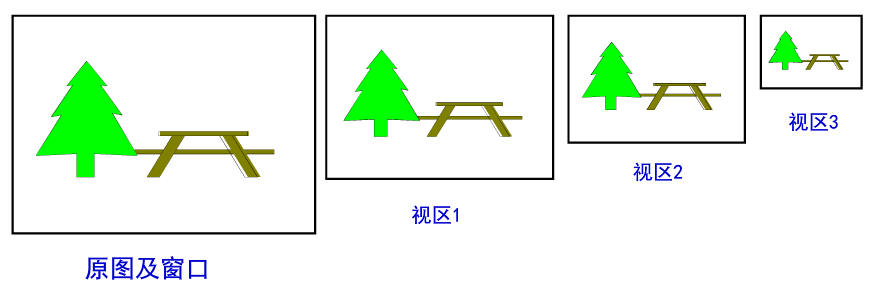
若把一个固定大小的窗口在一幅大图形上移动,视区不变会产生【漫游效果】。
3、窗口到视区的变换
窗口到视区的【映射】是【基于一个等式】,即对每一个在世界坐标下的点(x,y),产生屏幕坐标系中的一个点(sx,sy)
这个映射是“保持比例”的映射——>使得这个映射有线性形式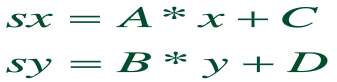
其中A、B、C、D是常数
首先考虑x的映射,保持比例的性质说明: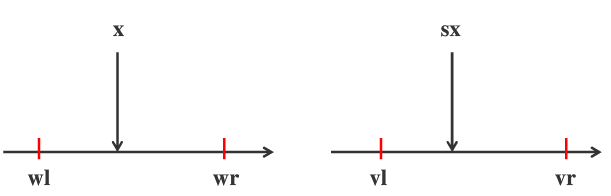

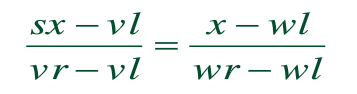

又因为
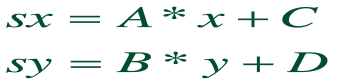
,可知:A看作放大x的部分,C看作常数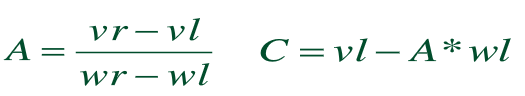
同理,y方向上保持比例性质满足: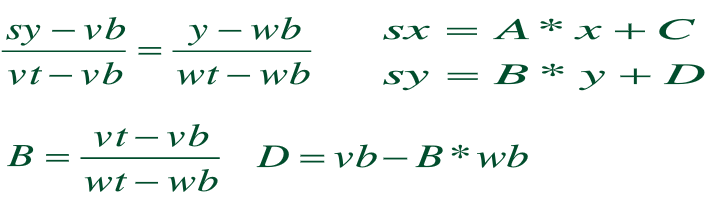
这个映射可用于【任意点(x,y)】,不管它是否在窗口之中。
在窗口【中】的点映射到视区【中】的点,在窗口【外】的点映射到视区【外】的点。