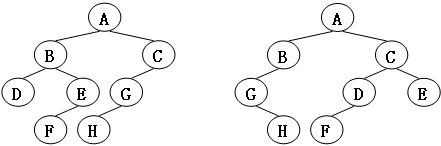
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
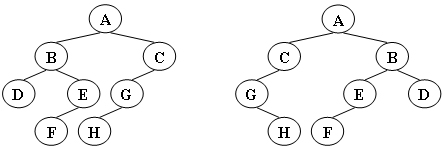
图1
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No思路:
- 二叉树的表示:结构数组表示二叉树——静态链表(物理上的存储是数组,但是是一种链表思想)。
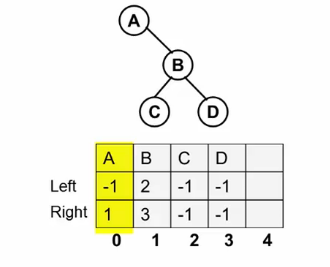
- 建二叉树,寻找根结点,在任何结点的左右儿子中都没出现的结点就是根结点。
- 判别同构,注意分情况讨论。
//都为空
//一个空一个不空
//两个都不空
根结点的元素不一样(根结点位置是随机的)
根结点的元素一样,分别判断左右儿子
- 注意,Root要初始化,否则空树的测试点不通过。
1 #include <iostream> 2 using namespace std; 3 #define MAXSIZE 10 4 #define ElementType char 5 #define Tree int 6 #define Null -1//注意与链表中NULL(0)的区别 7 8 //二叉树的表示 9 struct TreeNode 10 { 11 ElementType Data; 12 Tree Left;//表示左儿子的下标而不是指针 13 Tree Right; 14 }T1[MAXSIZE],T2[MAXSIZE];//建立两个结构体数组 15 16 //建一棵树 17 Tree BuildTree(struct TreeNode T[]) { 18 int n,Root=Null; 19 char cl, cr; 20 int check[MAXSIZE] = { 0 }; 21 cin >> n; 22 for (int i = 0; i < n; i++) { 23 cin >> T[i].Data >> cl >> cr; 24 if (cl != '-') { 25 T[i].Left = cl - '0'; 26 check[cl - '0'] = 1; 27 } 28 else 29 T[i].Left = Null; 30 if (cr != '-') { 31 T[i].Right = cr - '0'; 32 check[cr - '0'] = 1; 33 } 34 else 35 T[i].Right = Null; 36 } 37 for (int i = 0; i < n; i++) { 38 if (check[i] == 0) { 39 Root = i; 40 break; 41 } 42 } 43 return Root; 44 } 45 46 //判断同构 47 int Isomorphic(Tree R1, Tree R2) { 48 if (R1 == Null && R2 == Null) 49 return 1; 50 if ((R1 == Null && R2 != Null) || (R1 != Null && R2 == Null)) 51 return 0; 52 if (T1[R1].Data!=T2[R2].Data) 53 return 0; 54 if ((T1[R1].Left == Null) || T2[R2].Data == Null) 55 return(Isomorphic(T1[R1].Right, T2[R2].Right)); 56 if ((T1[R1].Left == Null && T2[R2].Left == Null) || (T1[R1].Left != Null && T2[R2].Left != Null && T1[T1[R1].Left].Data == T2[T2[R2].Left].Data)) 57 return (Isomorphic(T1[R1].Right, T2[R2].Right)); 58 else return (Isomorphic(T1[R1].Left, T2[R2].Right) && Isomorphic(T1[R1].Right, T2[R2].Left)); 59 } 60 61 62 int main() 63 { 64 Tree R1, R2;//树的根结点 65 R1 = BuildTree(T1); 66 R2 = BuildTree(T2); 67 if (Isomorphic(R1, R2)) 68 cout << "Yes" << endl; 69 else 70 cout << "No" << endl; 71 return 0; 72 }