图的概念
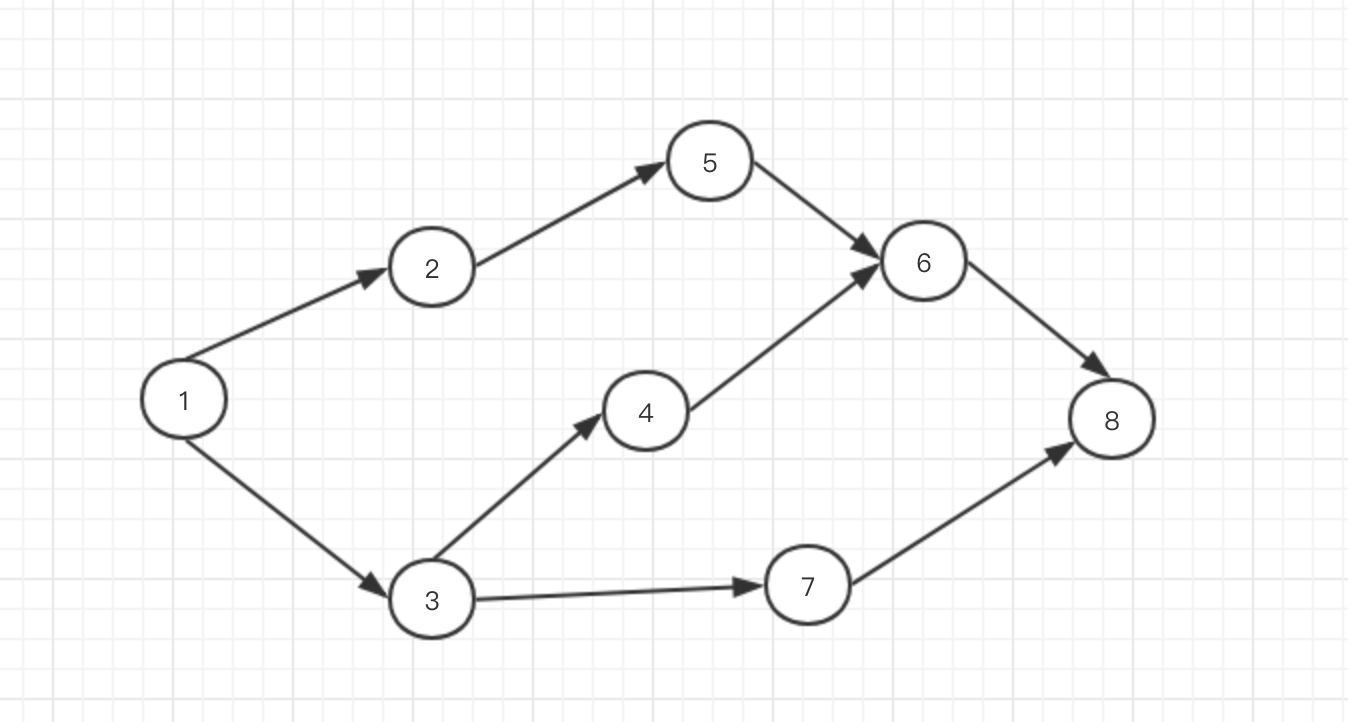
图表示的是多点之间的连接关系,由节点和边组成。类型分为有向图,无向图,加权图等,任何问题只要能抽象为图,那么就可以应用相应的图算法。
用字典来表示图
这里我们以有向图举例,有向图的邻居节点是要顺着箭头方向,逆箭头方向的节点不算作邻居节点。
在python中,我们使用字典来表示图,我们将图相邻节点之间的连接转换为字典键值之间的映射关系。比如上图中的1的相邻节点为2和3,即可表示如下:
graph={}
graph[1] = [2,3]
按照这种方式,上图可以完整表示为:
graph={}
graph[1] = [3,2] # 这里为了演示,调换一下位置
graph[2] = [5]
graph[3] = [4,7]
graph[4] = [6]
graph[5] = [6]
graph[6] = [8]
graph[7] = [8]
graph[8] = []
如此我们将所有节点和其相邻节点之间的连接关系全部描述一遍就得到了图的字典表示形式。节点8由于没有相邻节点,我们将其置为空列表。
广度优先搜索
广度优先搜索和深度优先搜索是图遍历的两种算法,广度和深度的区别在于对节点的遍历顺序不同。广度优先算法的遍历顺序是由近及远,先看到的节点先遍历。
接下来使用python实现广度优先搜索并找到最短路径:
from collections import deque
from collections import namedtuple
def bfs(start_node, end_node, graph): # 开始节点 目标节点 图字典
node = namedtuple('node', 'name, from_node') # 使用namedtuple定义节点,用于存储前置节点
search_queue = deque() # 使用双端队列,这里当作队列使用,根据先进先出获取下一个遍历的节点
name_search = deque() # 存储队列中已有的节点名称
visited = {} # 存储已经访问过的节点
search_queue.append(node(start_node, None)) # 填入初始节点,从队列后面加入
name_search.append(start_node) # 填入初始节点名称
path = [] # 用户回溯路径
path_len = 0 # 路径长度
print('开始搜索...')
while search_queue: # 只要搜索队列中有数据就一直遍历下去
print('待遍历节点: ', name_search)
current_node = search_queue.popleft() # 从队列前边获取节点,即先进先出,这是BFS的核心
name_search.popleft() # 将名称也相应弹出
if current_node.name not in visited: # 当前节点是否被访问过
print('当前节点: ', current_node.name, end=' | ')
if current_node.name == end_node: # 退出条件,找到了目标节点,接下来执行路径回溯和长度计算
pre_node = current_node # 路径回溯的关键在于每个节点中存储的前置节点
while True: # 开启循环直到找到开始节点
if pre_node.name == start_node: # 退出条件:前置节点为开始节点
path.append(start_node) # 退出前将开始节点也加入路径,保证路径的完整性
break
else:
path.append(pre_node.name) # 不断将前置节点名称加入路径
pre_node = visited[pre_node.from_node] # 取出前置节点的前置节点,依次类推
path_len = len(path) - 1 # 获得完整路径后,长度即为节点个数-1
break
else:
visited[current_node.name] = current_node # 如果没有找到目标节点,将节点设为已访问,并将相邻节点加入搜索队列,继续找下去
for node_name in graph[current_node.name]: # 遍历相邻节点,判断相邻节点是否已经在搜索队列
if node_name not in name_search: # 如果相邻节点不在搜索队列则进行添加
search_queue.append(node(node_name, current_node.name))
name_search.append(node_name)
print('搜索完毕,最短路径为:', path[::-1], "长度为:", path_len) # 打印搜索结果
if __name__ == "__main__":
graph = dict() # 使用字典表示有向图
graph[1] = [3, 2]
graph[2] = [5]
graph[3] = [4, 7]
graph[4] = [6]
graph[5] = [6]
graph[6] = [8]
graph[7] = [8]
graph[8] = []
bfs(1, 8, graph) # 执行搜索
搜索结果
开始搜索...
待遍历节点: deque([1])
当前节点: 1 | 待遍历节点: deque([3, 2])
当前节点: 3 | 待遍历节点: deque([2, 4, 7])
当前节点: 2 | 待遍历节点: deque([4, 7, 5])
当前节点: 4 | 待遍历节点: deque([7, 5, 6])
当前节点: 7 | 待遍历节点: deque([5, 6, 8])
当前节点: 5 | 待遍历节点: deque([6, 8])
当前节点: 6 | 待遍历节点: deque([8])
当前节点: 8 | 搜索完毕,最短路径为: [1, 3, 7, 8] 长度为: 3
广度优先搜索的适用场景:只适用于深度不深且权值相同的图,搜索的结果为最短路径或者最小权值和。
深度优先搜索
深度优先搜索的遍历顺序为一条路径走到底然后回溯再走下一条路径,这种遍历方法很省内存但是不能一次性给出最短路径或者最优解。
用python实现深度优先算法只需要在广度的基础上将搜索队列改为搜索栈即可:
from collections import deque
from collections import namedtuple
def bfs(start_node, end_node, graph):
node = namedtuple('node', 'name, from_node')
search_stack = deque() # 这里当作栈使用
name_search = deque()
visited = {}
search_stack.append(node(start_node, None))
name_search.append(start_node)
path = []
path_len = 0
print('开始搜索...')
while search_stack:
print('待遍历节点: ', name_search)
current_node = search_stack.pop() # 使用栈模式,即后进先出,这是DFS的核心
name_search.pop()
if current_node.name not in visited:
print('当前节点: ', current_node.name, end=' | ')
if current_node.name == end_node:
pre_node = current_node
while True:
if pre_node.name == start_node:
path.append(start_node)
break
else:
path.append(pre_node.name)
pre_node = visited[pre_node.from_node]
path_len = len(path) - 1
break
else:
visited[current_node.name] = current_node
for node_name in graph[current_node.name]:
if node_name not in name_search:
search_stack.append(node(node_name, current_node.name))
name_search.append(node_name)
print('搜索完毕,路径为:', path[::-1], "长度为:", path_len) # 这里不再是最短路径,深度优先搜索无法一次给出最短路径
if __name__ == "__main__":
graph = dict()
graph[1] = [3, 2]
graph[2] = [5]
graph[3] = [4, 7]
graph[4] = [6]
graph[5] = [6]
graph[6] = [8]
graph[7] = [8]
graph[8] = []
bfs(1, 8, graph)
搜索结果
开始搜索...
待遍历节点: deque([1])
当前节点: 1 | 待遍历节点: deque([3, 2])
当前节点: 2 | 待遍历节点: deque([3, 5])
当前节点: 5 | 待遍历节点: deque([3, 6])
当前节点: 6 | 待遍历节点: deque([3, 8])
当前节点: 8 | 搜索完毕,路径为: [1, 2, 5, 6, 8] 长度为: 4
python的deque根据pop还是popleft可以当成栈或队列使用,DFS的能够很快给出解,但不一定是最优解。
深度优先搜索的适用场景: 针对深度很深或者深度不确定的图或者权值不相同的图可以适用DFS,优势在于节省资源,但想要得到最优解需要完整遍历后比对所有路径选取最优解。