最长回文子串

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

 

Example:

Input: "cbbd"

Output: "bb"

 

分析：

方法一：暴力求解

　　遍历字符串，判断以每一个字符为起始的子串是否为回文字符串，记录起始位置和长度。这是最容易想到的方法，但是时间复杂度较大。

方法二：动态规划

　　p[i][j]表示以第i个字符开始，第j个字符结束的子串是否为回文字符串，p[i][j]=1表示是回文字符串，p[i][j]=0表示不是回文字符串。起始状态p[i][i]=1

转移方程为：p[i][j]=1 if p[i+1][j-1] == 1 and s[i]==s[j] else 0。此方法时间复杂度为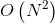

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        l = len(s)
        maxlen = 1
        start = 0
        p = [[0]*l for i in range(l)]
        for i in range(l):
            p[i][i]=1
            if i < l-1 and s[i] == s[i+1]:
                p[i][i+1] = 1
                maxlen = 2
                start = i
        for length in range(3,l+1):
            for i in range(l-length+1):
                j = i + length -1
                if p[i+1][j-1]==1 and s[i] == s[j]:
                    p[i][j] = 1
                    maxlen = length
                    start = i
        return s[start:start+maxlen]

 

方法三：中心扩展

　　把字符串中的每个字母作为中心，对称地向两边扩展，但要考虑两种情况，1、如aba，长度为奇数。2、如abba，长度为偶数的。这种方法的时间复杂度为

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        maxlen = 1
        start = 0
        for i in range(len(s)):
            j = i-1
            k = i+1
            while j>=0 and k <len(s) and s[j] == s[k]:
                if k-j+1 >= maxlen:
                    maxlen = k-j+1
                    start = j
                j -= 1
                k += 1
        for i in range(len(s)):
            j = i
            k = i+1
            while j >= 0 and k < len(s) and s[j] == s[k]:
                if k-j+1 >= maxlen:
                    maxlen = k-j+1
                    start = j
                j -= 1
                k += 1
        return s[start:start+maxlen]