如何把SVM的推导和损失函数联系起来？

1：

作者：PENG
链接：https://www.zhihu.com/question/62881491/answer/203113850
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

从不同的角度来看SVM可以得到两种不同的解释。

通常来讲SVM是为了找到具有最大间隔的超平面，而这个最大间隔由 决定，而所有样本点是需要满足一个约束条件 的，这是一个有约束的优化问题，因而优化目标 适用于对偶+拉格朗日乘数法来解决。

当我们允许有某些错误样本出现的时候，就需要考虑到希望有尽量少的不满足约束的点，因而为这些“坏点”定义一个惩罚项，优化目标就可以转变为 。如果把后面的这个惩罚项换成 就变成了经典形式的SVM。

从另外的角度来看是指将模型最后的预测值与ground truth的误差当作优化目标，我们需要学习出参数 , 使得误差最小。

例如在二分类SVM中，我们希望当样本点满足 时，预测 ，而 时，我们预测 ，但是这样还不太可靠，如果我们想提高模型预测的置信度，我们可以定义一个margin ,使得 时判断 （负例同理，因而联立起来变为 ），当样本点没有满足这个条件的时候，就会有损失，合理的方式就是使用hinge loss损失函数 ，而这时问题就变为了一个无约束的优化问题。

而为了使模型泛化性能更好，我们加上正则项 ，损失函数就变成了 ，这时可以看出从这种角度出发得到目标函数和和前面相同了，而且这种情况下使用简单的梯度下降就可以进行优化。

 

 

2：

 

作者：李欣宜
链接：https://www.zhihu.com/question/62881491/answer/500947075
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

谢谢

@林高遠

的邀请。但是对不起，我不是做机器学习的，读的和做的都很少，不太明白这个问题的意思，只能按照我的理解尝试揣测一下这个观点。

最近看到了关于SVM的损失函数，在衔接这两部分是大家都在用这么一句话“SVM的训练也可以从另一个角度来理解”引出Hinge

抱歉我没有见过这个说法。请你给出这个文本的出处，否则我无法精确的理解它想表达什么。

 

所谓soft-margin SVM，相比hard-margin SVM我们允许某些用于训练的样本点在模型中被错误分类，主要是为了防止过分追求模型和训练样本的贴合而引发的overfit。那么去考虑soft-margin SVM的模型，就必须思考怎样地去“允许”SVM在一些训练样本上出错，

1. 一方面希望margin尽可能的大以留出余地防止overfit

2. 一方面又希望它在训练样本上的表现足够准确

那么需要的目标函数就有两个部分，1对应的是 ，就是我们在hard-margin SVM中见到的目标函数。问题在于如何表达2？如何量化SVM即分类函数 对于训练样本点的分类误差？那么这里需要定义一个loss function，让你来写你怎么写？

离散的用 表示如果该点分类正确则产生的loss为0否则为1，这个粗糙的写法使得整个目标函数非凸，不连续，数学性质差，难以直接优化。所以会用一些性质比较好的凸函数替代，hinge函数就是其中一个

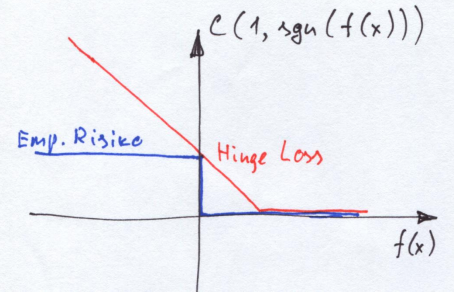蓝色的线为原始的0/1损失函数，红色的为hinge loss，大致看下形状就行

这里的 表示未经过取符号处理的原始预测结果与样本标签的乘积 ，这个表达式在hard-margin SVM模型中也是出现过的

在往回想它的推导过程，我们需要一个超平面（在特征空间只有一维 ，如下图，这个超平面就是一条直线）分割一些标签为+1和-1的样本点，并且为了留出足够的准确性，希望样本点都距离这个超平面远一些。那么这个问题可以表达为：找到一个超平面，使在某个等距的间隔内没有样本点，而且在同一侧的样本点的标签相同，并使得这个间隔最大。那个不等式约束的含义就是保证样本点在图中对应虚线的外侧。

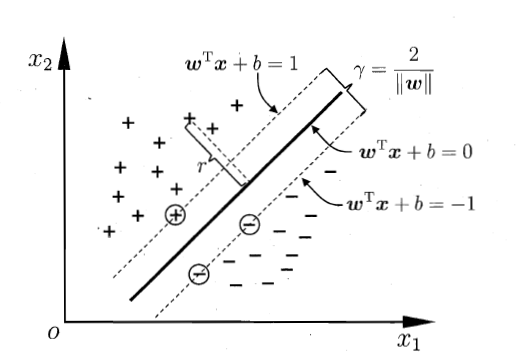两条虚线之间的距离就是margin，标签为+的点全部在wx+b=1的上方，即wx+b>=0，标签为-的点全在wx+b=-1的下方，即wx+b<=-1，取到等号的，即圈出来的样本点就是所谓的support vector，用于支撑起margin

回到soft-margin模型，当然使用hinge loss时一般用的是slack variable 来表示样本点 在当前训练模型下的violate，即

虽然被写在约束不等式中，但对于固定的w和b来说，它的取值就是定值即hinge loss的结果。这是min这个目标决定的。 的物理意义也可以被看作样本点i如果没有在虚线外侧（包括在实线正确的一侧，却不在虚线的外侧）时，它离它“应该”在的位置的距离（实际上还需要除以 ），即该点到该虚线的距离。C是一个调整惩罚权重的参数。

众所周知，两种SVM的Lagrange dual problem形式几乎一致，除了soft-margin对Lagrange multiplier 的不等式约束为 而hard-margin的约束为 ,这时hinge loss的形式天然的符合SVM模型，它们之间微妙的关系也呼之欲出了。

 

这样还不明显不妨退回去看两个SVM的原始形式，一起推一下他们的Lagrange dual形式，首先hard-margin的Lagrange function写为

而soft-margin则为

多出了与 相关的最后一项，这样写会发现 在函数中似乎也担当了类似于Lagrange multiplier的角色。不要忘了本来就有 ，虽然这一点也可以直接从上面的优化目标和约束推出，并体现在KKT conditions之一的 和 上，决定SVM的还是令 的那几个样本点，即support vector

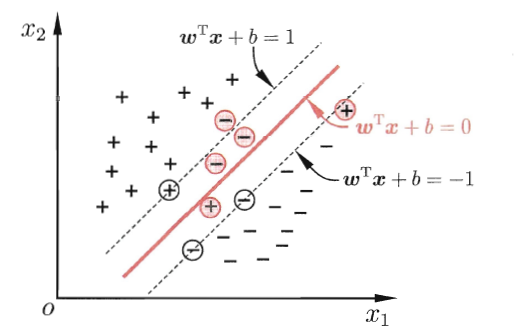
图中被圈起来的就是使得alpha_i>0的那些样本点，即support vector，被方形圈住的是没有违法超平面分类的SV，它们的hinge function结果为0，三角形的样本点则是违反了分类函数的SV，它们的hinge functor大于0

此时有 ，这部分的取值在hinge loss的函数图像上是分段函数中的一部分，即 ，取等号的即free SV，就像hard-margin问题中的所有SV，而斜率为-1的直线上的其他部分即违法margin分类的bounded SV，这两类SV共同决定了SVM模型的参数；而远离margin的，分类正确的样本点，在hinge loss的图像上落在贴行于z轴的地面上，没人关心它们的函数值统一截取为0，正如在样本空间中也没人关心它们的存在，再添加一个这样样本点进来也不会改变已经训练结束的SVM模型的参数。换言之，hinge保存了SVM的稀疏性和持续训练的低开销。

 

hinge是一种naive且常用的loss function，符合空间直觉和逻辑，使用hinge loss的soft-margin可以看成原问题hard-margin最简单的一种扩展。除此之外还有很多的loss function，比如exponential loss和logistic loss，只是把当前训练中模型输出的数值结果 用其他函数映射成另一个损失值，相比线性的hinge，就不能用上面的slack variable去做了，Lagrange multiplier method的结果也不会像上面那样与hard-margin问题相似和整洁了，但这些loss的计算也各有长处，比如logistic loss可以用于L2-regularized logistic regression，输出结果也更具概率的自然意义。

 

原文：https://www.zhihu.com/question/62881491?sort=created