线性表和树两类数据结构，线性表中的元素是“一对一”的关系，树中的元素是“一对多”的关系，本章所述的图结构中的元素则是“多对多”的关系。图（Graph）是一种复杂的非线性结构，在图结构中，每个元素都可以有零个或多个前驱，也可以有零个或多个后继，也就是说，元素之间的关系是任意的。
一、图的定义与术语
定义：图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
1、图的分类
图是按照无方向和有方向分为无向图和有向图。
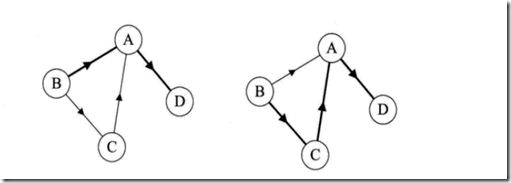
左图为无向图是由顶点和边构成，右图为有向图是由顶点和弧（有向边构成）。弧有弧头和弧尾区别。
按照边分为稀疏图和稠密图，这是个模糊的概念，同样是相对的概念。
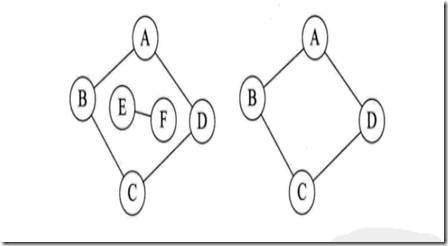
如果任意两个顶点之间都存在边叫完全图，有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图。在用数学方式表示时，无向边用()表示，有向边用<>表示。现在我们讲解的图全是简单图。
左图没有重复的边或者到自身的边（简单图），右图则有。
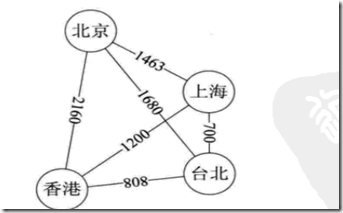
这种边带权值的图叫网
2.图的顶点和边间关系
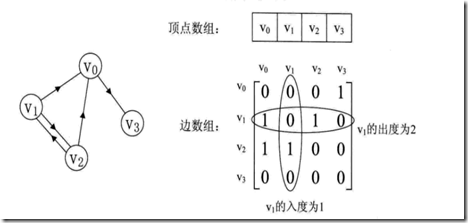
顶点的度：顶点关联边的数目。有向图图中有，入度：方向指向顶点的边；出度：方向背向顶点的边。在有向图中顶点的度就是两者之和。
路径长度：路径上边或者弧的数目。
左图中，从B到D的路径度为2，在右图中就是3了（粗线的边）。
右图中A的入度是2，出度是1；B的入度为0，出度是2.
连通
在无向图G中，任意两个顶点是相通的就是连通图。
左图不是连通图，AE之间没有连通。
二、图的存储结构
图的结构比价复杂，任意两个顶点之间都可能存在关系，不能用简单的顺序存储结构来表示。如果运用多重链表，即一个数据域多个指针域组成的结点表示图中一个结点，则造成大量存储单元浪费。
1、邻接矩阵
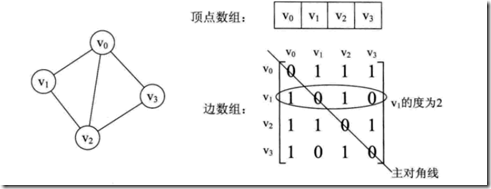
邻接矩阵用两个数组保存数据。一个一维数组存储图中顶点信息，一个二维数组存储图中边或弧的信息。
无向图中二维数组是个对称矩阵。
特点：
- 1、0表示无边，1表示有边
2、顶点的度是行内数组之和。
3、求取顶点邻接点，将行内元素遍历下。
有向图的邻接矩阵：有向图中讲究入度和出度，各行之和是出度，各列之和是入度。
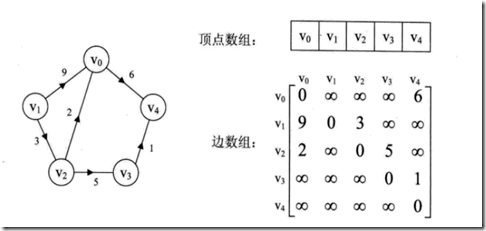
带权的图叫网，用邻接矩阵表示为：
邻接矩阵对于边数相对顶点较少的图，就是对存储空间极大的浪费。
2、邻接表
邻接表：数组和链表相结合的存储方法为邻接表。
- 图中顶点用一个一维数组存储。
- 图中每个顶点Vi的所有邻接点构成一个线性表。
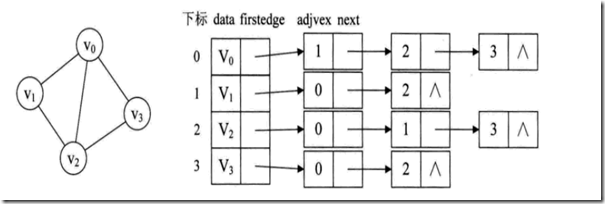
从图中得知，顶点表的各个结点由data和Firstedge两个域表示，data是数据域，存储顶点信息，firstedge是指针域，指向边表的第一个结点，即顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中坐标，next存储边表中下一个结点指针。比如v1顶点与v2、v0互为邻接点，则在v1边表中，adjvex分别为0和2。
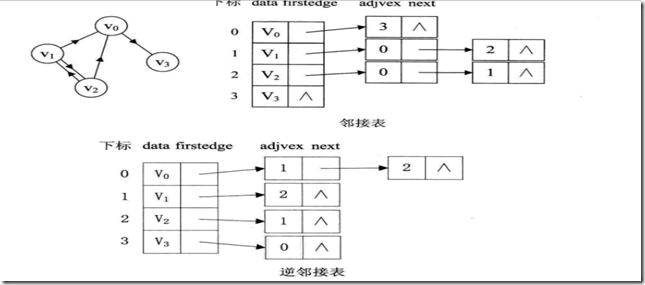
有向图也可以用邻接表，出度表叫邻接表，入度表尾逆邻接表。
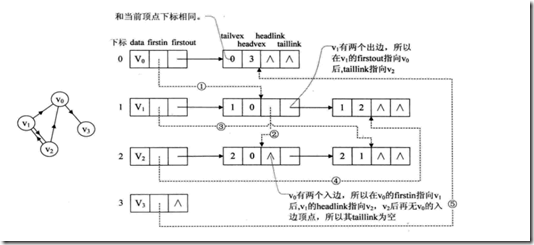
3、十字链表
在邻接表中针对有向图，分为邻接表和逆邻接表，导致无法从一个表中获取图的入读和出度的情况，有人提出了十字链表。
定点表：
其中firstin：入边表头指针，指向顶点入边表的第一个结点。
firstout：出边表头指针，指向顶点出边表第一个结点。
边表：
其中tailvex是指弧起点在顶点表的下标，headvex弧终点在顶点表的下标，headlink入边表指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边。
4、邻接多重表
邻接多重表结构如图：
ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。ilink指向依附项点ivex的下一条边，jlink指向依附顶点jvex的下一条边。
三 、代码实现
Graphdata.h -
GraphData.cpp TestGraph
http://www.cnblogs.com/polly333/p/4760275.html